高中 数学
若函数f(x)=x2+  为偶函数,则实数a=.
为偶函数,则实数a=.
 为偶函数,则实数a=.
为偶函数,则实数a=.
下列函数中,既是偶函数又在(0,+∞)单调递增的函数是( )
A .  B . y=|x|+1
C .
B . y=|x|+1
C .  D . y=2-|x|
D . y=2-|x|
 B . y=|x|+1
C .
B . y=|x|+1
C .  D . y=2-|x|
D . y=2-|x|
已知数列  的首项
的首项  ,数列
,数列  为等比数列,且
为等比数列,且  .若b10b11=2,则
.若b10b11=2,则  ( )
( )
 的首项
的首项  ,数列
,数列  为等比数列,且
为等比数列,且  .若b10b11=2,则
.若b10b11=2,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若不等式  的解集恰为不等式
的解集恰为不等式  的解集,则a-b=( )
的解集,则a-b=( )
 的解集恰为不等式
的解集恰为不等式  的解集,则a-b=( )
的解集,则a-b=( )
A . 3
B . -3
C . 5
D . -5
《九章算术》中的“两鼠穿墙题”是我国数学的古典名题:“今有垣厚若干尺,两鼠对穿,大鼠日一尺,小鼠也日一尺,大鼠日自倍,小鼠日自半.问何日相逢,各穿几何?题意是:有两只老鼠从墙的两边打洞穿墙,大老鼠第一天进一尺,以后每天加倍;小老鼠第一天也进一尺,以后每天减半”,如果墙厚  ,天后两只老鼠打穿城墙.
,天后两只老鼠打穿城墙.
 ,天后两只老鼠打穿城墙.
,天后两只老鼠打穿城墙.
观察下列各式:72=49,73=343,74=2401,…,则72016的末两位数字为( )
A . 01
B . 43
C . 07
D . 49
如图,矩形  中,
中,  ,
,  ,E为
,E为  的中点,将
的中点,将  沿
沿  翻折,得到四棱锥
翻折,得到四棱锥  .
.
 中,
中,  ,
,  ,E为
,E为  的中点,将
的中点,将  沿
沿  翻折,得到四棱锥
翻折,得到四棱锥  .
. 
-
(1) 证明:
 ;
;
-
(2) 在①直线
 与平面
与平面  所成角为
所成角为  ,②若
,②若  交
交  于O,
于O,  的面积为
的面积为  ,③
,③ 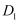 到平面
到平面  的距离为
的距离为  ,这三个条件中任选一个,补充在下面的问题中,并解决该问题:已知 ▲ , 求锐二面角
,这三个条件中任选一个,补充在下面的问题中,并解决该问题:已知 ▲ , 求锐二面角  的余弦值.
的余弦值.
f(x)=  是定义在(﹣∞,+∞)上是减函数,则a的取值范围是( )
是定义在(﹣∞,+∞)上是减函数,则a的取值范围是( )
 是定义在(﹣∞,+∞)上是减函数,则a的取值范围是( )
是定义在(﹣∞,+∞)上是减函数,则a的取值范围是( )
A . [ 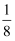 ,
,  )
B . [0,
)
B . [0,  ]
C . (0,
]
C . (0,  )
D . (﹣∞,
)
D . (﹣∞,  ]
]
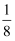 ,
,  )
B . [0,
)
B . [0,  ]
C . (0,
]
C . (0,  )
D . (﹣∞,
)
D . (﹣∞,  ]
]
求下列函数的值域:
-
(1)
 ;
;
-
(2)
 .
.
已知函数  ,其中
,其中  为奇函数,
为奇函数,  为偶函数.
为偶函数.
 ,其中
,其中  为奇函数,
为奇函数,  为偶函数.
为偶函数.
-
(1) 求
 与
与  的解析式;
的解析式;
-
(2) 当
 时,
时,  有解,求实数
有解,求实数  的取值范围.
的取值范围.
命题“任意实数  ,都有
,都有 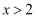 ”的否定是( )
”的否定是( )
 ,都有
,都有 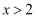 ”的否定是( )
”的否定是( )
A . 对任意实数  ,都有
,都有  B . 不存在实数
B . 不存在实数  ,使
,使  C . 对任意非实数
C . 对任意非实数  ,都有
,都有  D . 存在实数
D . 存在实数  ,使
,使 
已知f(x)=ex﹣ax﹣1.
-
(1) 求f(x)的单调递增区间;
-
(2) 若f(x)在定义域R内单调递增,求a的取值范围.
下列函数是奇函数,且在  上单调递增的是( )
上单调递增的是( )
 上单调递增的是( )
上单调递增的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列各组数的大小比较正确的是( )
A . 2  <(
<(  )3
B . (
)3
B . ( 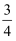 )
)  >(
>( 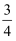 )
)  C . 53.1<33.1
D . 0.3
C . 53.1<33.1
D . 0.3  >0.3
>0.3 
 <(
<(  )3
B . (
)3
B . ( 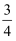 )
)  >(
>( 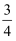 )
)  C . 53.1<33.1
D . 0.3
C . 53.1<33.1
D . 0.3  >0.3
>0.3 
如图所示,在矩形![]() 中,
中,![]() ,
,![]() ,图中阴影部分是以
,图中阴影部分是以![]() 为直径的半圆,现在向矩形
为直径的半圆,现在向矩形![]() 内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )
内随机撒4000粒豆子(豆子的大小忽略不计),根据你所学的概率统计知识,下列四个选项中最有可能落在阴影部分内的豆子数目是( )

A.1000 B.2000 C.3000 D.4000
若复数z满足z(1-i)=2i(i是虚数单位),![]() 是z的共轭复数,则z·
是z的共轭复数,则z·![]() = .
= .
一般吧数字出现的规律满足如图的模型称为蛇形模型:数字1出现在第1行,数字2,3出现在第2行;数字6,5,4(从左到右)出现在第3行;数字7,8,9,10出现在第4行,以此类推,第21行从左到右的第4个数字应是 .

在体积为![]() 的球的表面上有A,B,C三点,AB=1,BC=
的球的表面上有A,B,C三点,AB=1,BC=![]() ,A,C两点的球面距离为
,A,C两点的球面距离为![]() ,则球心到平面ABC的距离为 ( )
,则球心到平面ABC的距离为 ( )
A.![]() B.
B.![]() C.
C.![]() D.1
D.1
设集合![]() 的元素个数为15个,则a可取值的最小自然数为
的元素个数为15个,则a可取值的最小自然数为
A.136 B.144 C.145 D.154
已知p:x≥k,q:![]() <1,如果p是q的充分不必要条件,则实数k的取值范围是 ( )
<1,如果p是q的充分不必要条件,则实数k的取值范围是 ( )
A.(2,+∞) B.[2,+∞) C.[1,+∞) D.(-∞,-1)
最近更新
- 太阳系有八大行星,按体积和质量对它们进行分类,地球属于: A.类地行星 B.巨行星 C.远日行星
- 如图所示,在竖直平面内的直角坐标系中,一个质量为m的质点在外力F的作用下,从坐标原点O由静止沿直线ON斜向下运动,直线O
- 阅读下面的文字,完成第12~15题。(12分) 那条河流 我怀念那条河。 远远地看,它就像一根孤独的琴弦绷在原野上,任风
- 阅读下面文字,完成小题。 品 质 格斯拉先生的店房朴素安静,橱窗里陈列的几双靴子太美观了,是模范品,只有亲眼看过靴子
- 秦始皇建立的中央集权制度最重要的原则是 ( ) A.“天下之事,无大小,皆决于上” B.“节用裕民……以
- 阅读下文,完成文后各题。 诗的含蓄美 吴战垒 古人有“言不尽意”之说,语言本来是传达思想情感的工具,但有些微妙的思想情感
- 单项选择 It’s too hot, would you mind the windows? A. tocl
- 历史上大凡激烈变革和动荡的时代,总不免出现两种倾向:一种是要砸烂一切旧传统的革命倾向,一种是要维护旧传统的保守倾向。中国
- 根据下图中所发生的化学反应现象及化学反应原理进行归纳并回答下列问题:(1)所反生的三个反应有许多共同特点,分别是(只答四
- 某小型实验水电站输出功率是20kW,输电线路总电阻是6Ω。(1)若采用380V输电,求输电线路损耗的功率。(2)若改用5
- 议会制共和制和总统制是当代资本主义国家的两种主要政体.其区别是 ①前者不设总统,后者设立总统 ②前者的政府对议会负
- 我国人口的突出特点是() A. 人口基数大,人口增长快 B. 人口基数
- (5分)低碳经济是一种以低能耗和高效能等为主要特征、排放较少的温室气体并获得较大产出的新经济发展模式。(1)温室气主要是
- 关于黄河沿岸各省地理事物的叙述,错误的是A.青海省有“江河之源”的称号B.河南省号称“天下之中”,古都最多C.陕西省被称
- 下图是沿某一纬线方向的某国家地形剖面图,这个国家可能是:A.俄罗斯 B.巴西 C
- 可以证明次氯酸为弱酸的实验事实是( )A.次氯酸具有强氧化性B.次氯酸不稳定,见光即分解C.可与强碱发生中和反应D
- 关于板块构造学说的说法,正确的是( ) A.认为地壳被不同的构造带分割成许多单元,即板块 B.板块漂浮在软流层之
- 铁镍蓄电池又称爱迪生电池,放电时的总反应为:Fe+Ni2O3+3H2O=Fe(OH)2+2Ni(OH)2 。下列有关该电
- 权力的高度集中是秦朝政治制度的基本特征,这造成深远的历史影响包括( ) ①君权与相权矛盾重重 ② 中央与地方斗争激
- 两个相同的LC振荡电路,充电电压分别为U1和U2,且U1=2U2,则它们的振荡周期T1和T2的关系为( )A.T1



