高中 数学
双曲线 , 左右焦点分别为
, 左右焦点分别为 , 过
, 过 作垂直于
作垂直于 轴的直线交双曲线于
轴的直线交双曲线于 两点,
两点, 的内切圆圆心为
的内切圆圆心为 ,
,  的内切圆圆心为
的内切圆圆心为 , 则四边形
, 则四边形 的面积是( )
的面积是( )
 , 左右焦点分别为
, 左右焦点分别为 , 过
, 过 作垂直于
作垂直于 轴的直线交双曲线于
轴的直线交双曲线于 两点,
两点, 的内切圆圆心为
的内切圆圆心为 ,
,  的内切圆圆心为
的内切圆圆心为 , 则四边形
, 则四边形 的面积是( )
的面积是( )
A . 8
B . 6
C . 4
D . 2
若不等式 的一个充分条件为
的一个充分条件为 , 则实数a的最小值是.
, 则实数a的最小值是.
 的一个充分条件为
的一个充分条件为 , 则实数a的最小值是.
, 则实数a的最小值是.
已知全集U={1,2,3,4,5,6,7,8},集合M={2,3,4},P={1,3,6},则集合{5,7,8}是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,则cosα﹣sinα=,sin2α=.
,则cosα﹣sinα=,sin2α=.
 ,则cosα﹣sinα=,sin2α=.
,则cosα﹣sinα=,sin2α=.
下列双曲线中,焦点在y轴上且渐近线方程为y=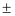 2x的是()
2x的是()
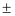 2x的是()
2x的是()
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设数列  的前
的前  项和
项和  ,满足
,满足  .
.
 的前
的前  项和
项和  ,满足
,满足  .
.
-
(1) 记
 ,求数列
,求数列  的前
的前  项的和
项的和  ;
;
-
(2) 记
 ,求数列
,求数列  的前
的前  项和
项和  .
.
已知  是角
是角  终边上一点.
终边上一点.
 是角
是角  终边上一点.
终边上一点.
-
(1) 求
 ,
,  ,
,  的值;
的值;
-
(2) 求
 的值.
的值.
设函数f(x)=cos(2x+ )+2cos2x,x∈R.
)+2cos2x,x∈R.
 )+2cos2x,x∈R.
)+2cos2x,x∈R.(Ⅰ)求函数f(x)的最小正周期和单调减区间;
(Ⅱ)将函数f(x)的图象向右平移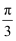 个单位长度后得到函数g(x)的图象,求函数g(x)在区间
个单位长度后得到函数g(x)的图象,求函数g(x)在区间 上的最小值.
上的最小值.
某企业有2个分厂生产某种零件,为了研究两个分厂生产零件的质量是否有差异,随机从2个分厂生产的零件中各抽取了500件,具体数据如下表所示:
| 甲厂 | 乙厂 | 总计 | |
| 优质品 | 360 | 320 | 680 |
| 非优质品 | 140 | 180 | 320 |
| 总计 | 500 | 500 | 1000 |
根据表中数据得  的观测值
的观测值  ,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
,从而断定两个分厂生产零件的质量有差异,那么这种判断出错的最大可能性为( )
附表:
| | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
A . 0.1
B . 0.01
C . 0.05
D . 0.001
函数  在点
在点  处的切线方程为
处的切线方程为  ,则
,则  .
.
 在点
在点  处的切线方程为
处的切线方程为  ,则
,则  .
.
已知函数 

-
(1) 求
 的值
的值
-
(2) 求
 单调递减区间
单调递减区间
四棱锥P﹣ABCD的底面是一个正方形,PA⊥平面ABCD,PA=AB=2,E是棱PA的中点,则异面直线BE与AC所成角的余弦值是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知直线l,m,平面α,β满足l⊥α,m⊂β,则“l⊥m”是“α∥β”的( )
A . 充要条件
B . 充分不必要条件
C . 必要不充分条件
D . 既不充分也不必要条件
已知函数  .
.
 .
.
-
(1) 当
 时,讨论函数
时,讨论函数  的单调性;
的单调性;
-
(2) 若函数
 在区间
在区间  上无零点,求
上无零点,求  的取值范围.
的取值范围.
已知数列  的前
的前  项和为
项和为  ,满足
,满足  ,且
,且  是
是  与
与  的等差中项.
的等差中项.
 的前
的前  项和为
项和为  ,满足
,满足  ,且
,且  是
是  与
与  的等差中项.
的等差中项.
-
(1) 求数列
 的通项公式
的通项公式  ;
;
-
(2) 若
 ,求数列
,求数列  的前
的前  项和
项和  .
.
已知集合A={x|log2x>m},B={x|﹣4<x﹣4<4}.
-
(1) 当m=2时,求A∪B,A∩B;
-
(2) 若A⊆∁RB,求实数m的取值范围.
命题“∃x>0,x2+x﹣2>0”的否定是.
![]() +80.25×
+80.25×![]() +(
+(![]() ×
× ![]() )6
)6
抛物线y=﹣2x2的焦点坐标是( )
A.(0,![]()
![]() ) B.(0,﹣
) B.(0,﹣![]()
![]() ) C.(
) C.(![]()
![]() ,0) D.(﹣
,0) D.(﹣![]()
![]() ,0)
,0)
若全集U=R,集合A=![]() ,B=
,B=![]() ,则
,则![]() =
=
A、![]() B、
B、![]()
C、![]() D、
D、![]()
最近更新
- 4.下列各句中没有语病的一项是() A.我国的环境保护规划从无到有,从简单到复杂,从局部到整体,目前形成了具有中国特色
- 如图,□ABCD中,AC=8,BD=6,AD=a,则a的取值范围是 .
- 已知下列反应的热化学方程式 6C(s)+5H2(g)+3N2(g)+9O2(g) 2C3H5(ONO2)3(l)
- 1932年,英国外交大臣奥斯汀·张伯伦在评论国际形势时说:“世界近两年正在倒退。各国相互之间不是更加接近,不是在增进友好
- 依据下面漫画寓意,下列事件背离经济全球化趋势的是①2009年2月,韩国对进口奶粉等婴儿用品免征3年增值税 ②2009年6
- 若cos(π+α)=﹣,π<α<2π,则sinα=
- 一定质量的理想气体经过一系列过程,如图8-2-15的所示,下列说法中正确的是( ) 图8-2-15A.a→b过程中
- 草酸(H2C2O4)又名乙二酸,是一种有机酸,易溶于水,广泛存在于植物源食品中。草酸不稳定,在浓硫酸的催化作用下,草酸固
- 某学生发现滴瓶中的溶液有悬浮物,拟用图所示操作进行过滤,操作上错误的地方有( ) A.4处
- 函数在一个周期内的图像如图所示,则此函数的解析式为( ) A. B. C.
- 关于酶的性质,下列叙述中错误的是( ) A.酶是活细胞产生的一类特殊的有机物,大多数为蛋白质,少数为RNA B.一
- 若方程x3-x+1=0在区间(a,b)(a、b是整数,且b-a=1)上有一根,则a+b=_________.
- 2009年网络热词“躲猫猫”、“钓鱼执法”、“被增长”、“被就业”等大部分来自于社会热点事件,彰显着中国公民意识的增强。
- 据报道,国家有关部门对家庭装饰材料进行抽查,发现具有毒气污染的材料占68%,它们会释放出300多种能引发30多种疾病的有
- (10分)某溶液中可能存在下列阴离子:Cl-、SO42-、CO32-中的一种或几种(1)当溶液中存在大量H+时,____
- There are many tall green trees on side of the street.
- Tom apiece of waste paper, and put it into the rubb
- 下列各句中,没有错别字的一项是 A.现在,素芭父母为操办她的婚姻大事而焦急不安,村人也到处遣责他们,甚至要把他们逐出种姓
- 如图,已知AB是⊙O的弦,OB=4,∠OBC=30°,C是弦AB上任意一点(不与点A、B重合),连接CO并延长CO交⊙O
- 从方框中选择适当的句子被全对话。 Tom: Whatare you going to be after leaving





