高中 数学
已知偶函数  在
在  上单调递增,且
上单调递增,且  ,则满足
,则满足  的x的取值范围是( )
的x的取值范围是( )
 在
在  上单调递增,且
上单调递增,且  ,则满足
,则满足  的x的取值范围是( )
的x的取值范围是( )
A .  B . [0,2]
C . [1,2]
D . [1,3]
B . [0,2]
C . [1,2]
D . [1,3]
若等比数列  的前
的前  项和
项和  ,则
,则  .
.
 的前
的前  项和
项和  ,则
,则  .
.
若 , 则下列结论正确的是( )
, 则下列结论正确的是( )
 , 则下列结论正确的是( )
, 则下列结论正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若直线  与直线
与直线  平行,则
平行,则  .
.
 与直线
与直线  平行,则
平行,则  .
.
已知抛物线  的焦点为
的焦点为  ,过点
,过点  且斜率为
且斜率为  的直线交抛物线于
的直线交抛物线于  两点,则线段
两点,则线段  的中点到
的中点到  轴的距离为( )
轴的距离为( )
 的焦点为
的焦点为  ,过点
,过点  且斜率为
且斜率为  的直线交抛物线于
的直线交抛物线于  两点,则线段
两点,则线段  的中点到
的中点到  轴的距离为( )
轴的距离为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
求下列椭圆的标准方程:
-
(1) 焦点在
 轴上,离心率
轴上,离心率  ,且经过点
,且经过点  ;
;
-
(2) 以坐标轴为对称轴,且长轴长是短轴长的3倍,并且过点
 .
.
设数列 是等差数列,其前n项和为
是等差数列,其前n项和为 , 若
, 若 ,
,  , 则
, 则 ( )
( )
 是等差数列,其前n项和为
是等差数列,其前n项和为 , 若
, 若 ,
,  , 则
, 则 ( )
( )
A . 31
B . 32
C . 33
D . 34
设命题p:函数y= 在定义域上为减函数;命题q:∃a,b∈(0,+∞),当a+b=1时,
在定义域上为减函数;命题q:∃a,b∈(0,+∞),当a+b=1时, +
+ =3,以下说法正确的是( )
=3,以下说法正确的是( )
 在定义域上为减函数;命题q:∃a,b∈(0,+∞),当a+b=1时,
在定义域上为减函数;命题q:∃a,b∈(0,+∞),当a+b=1时, +
+ =3,以下说法正确的是( )
=3,以下说法正确的是( )
A . p∨q为真
B . p∧q为真
C . p真q假
D . p,q均假
知函数f(x)=  (a>1),求:
(a>1),求:
 (a>1),求:
(a>1),求:
-
(1) 判断函数的奇偶性;
-
(2) 证明f(x)是R上的增函数;
-
(3) 求该函数的值域.
已知圆C:(x﹣a)2+y2=1,若直线l:y=x+a与圆C有公共点,且点A(1,0)在圆C内部,则实数a的取值范围是
对于函数y=f(x),如果存在区间[m,n],同时满足下列条件:①f(x)在[m,n]内是单调的;②当定义域是[m,n]时,f(x)的值域也是[m,n],则称[m,n]是该函数的“梦想区间”.若函数 存在“梦想区间”,则a的取值范围是( )
存在“梦想区间”,则a的取值范围是( )
 存在“梦想区间”,则a的取值范围是( )
存在“梦想区间”,则a的取值范围是( )
A . (1,3)
B . (0,2)
C .  D . (0,1)
D . (0,1)
 D . (0,1)
D . (0,1)
在数列{an}中,a1=﹣2,2an+1=2an+3,则a11等于( )
A .  B . 10
C . 13
D . 19
B . 10
C . 13
D . 19
在  内部任取一点
内部任取一点  ,使得
,使得  的面积与
的面积与  的面积的比值大于
的面积的比值大于  的概率为( )
的概率为( )
 内部任取一点
内部任取一点  ,使得
,使得  的面积与
的面积与  的面积的比值大于
的面积的比值大于  的概率为( )
的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知双曲线 的右焦点到它的一条渐近线的距离为4,且焦距为10,则该双曲线的渐近线方程为.
的右焦点到它的一条渐近线的距离为4,且焦距为10,则该双曲线的渐近线方程为.
 的右焦点到它的一条渐近线的距离为4,且焦距为10,则该双曲线的渐近线方程为.
的右焦点到它的一条渐近线的距离为4,且焦距为10,则该双曲线的渐近线方程为.
已知函数  的图象与直线
的图象与直线  恰有四个公共点
恰有四个公共点  ,
,  ,
,  ,
,  ,其中
,其中  ,则
,则  .
.
 的图象与直线
的图象与直线  恰有四个公共点
恰有四个公共点  ,
,  ,
,  ,
,  ,其中
,其中  ,则
,则  .
.
如图,四边形ABCD为菱形,∠ABC=120°,E , F是平面ABCD同一侧的两点,BE⊥平面ABCD , DF⊥平面ABCD , BE=2DF , AE⊥EC.

-
(1) 证明:平面AEC⊥平面AFC
-
(2) 求直线AE与直线CF所成角的余弦值
某公司生产一种产品,固定成本为  元,每生产一单位的产品,成本增加
元,每生产一单位的产品,成本增加 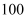 元,若总收入
元,若总收入  与年产量
与年产量  的关系是
的关系是  ,
,  ,则当总利润最大时,每年生产的产品单位数是( )
,则当总利润最大时,每年生产的产品单位数是( )
 元,每生产一单位的产品,成本增加
元,每生产一单位的产品,成本增加 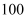 元,若总收入
元,若总收入  与年产量
与年产量  的关系是
的关系是  ,
,  ,则当总利润最大时,每年生产的产品单位数是( )
,则当总利润最大时,每年生产的产品单位数是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
为了得到函数 的图象,只要把函数
的图象,只要把函数 图象上所有的点( )
图象上所有的点( )
 的图象,只要把函数
的图象,只要把函数 图象上所有的点( )
图象上所有的点( )
A . 向右平移 个单位长度
B . 向左平移
个单位长度
B . 向左平移 个单位长度
C . 向左平移
个单位长度
C . 向左平移 个单位长度
D . 向右平移
个单位长度
D . 向右平移 个单位长度
个单位长度
 个单位长度
B . 向左平移
个单位长度
B . 向左平移 个单位长度
C . 向左平移
个单位长度
C . 向左平移 个单位长度
D . 向右平移
个单位长度
D . 向右平移 个单位长度
个单位长度
命题“![]() ”的否定为 ( )
”的否定为 ( )
(A) ![]() (B)
(B) ![]() (C)
(C) ![]() (D)
(D) ![]()
已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且
,且![]() .若数列
.若数列![]() 为递增数列,则实数
为递增数列,则实数![]() 的取值范围为( )
的取值范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 下列说法中错误的是 A.H3PO4的摩尔质量是98 g B.1 L 1 mol·L-1的MgCl2溶液中,Cl-的浓度为
- 阅读下面短文,根据以下提示:1)汉语提示 2)首字母提示 3)语境提示,在每个空格内填入一个适当的英语单词,并将该词完整
- 小明每天早上要在7:50之前赶到距家1 000m的学校上学.一天,小明以80m/min的速度出发,5min后,小明的爸爸
- 奇妙的克隆 1979年春,中国科学院武汉水生生物研究所的科学家,用鲫鱼囊胚期的细胞进行人工培养,经过385天59代连续传
- 下列关于光谱的说法正确的是( )A.炽热固体、液体和高压气体发出的光谱是连续光谱B.各种原子的线状谱中的明线和它的
- ----Tom, can you answer my question? ----Er, I’m sorry, M
- 在等差数列{an}中,公差d>0,其前n项和是Sn,a2a3=45,a1+a4=14.(1)求数列{an}的通项公式;(
- The British are not so familiar with different cultures and
- 1mol乙烯与氯气完全加成后再与氯气取代,整个过程最多需氯气为() A.1mol B.4mol
- 通过随机询问110名性别不同的大学生是否爱好某项运动,得到如下的列联表:男 女 合 计 爱好 40 20 60 不
- 下列几种常见的物质中,属于纯净物的是 A.食醋 B.碳酸氢铵 C.空气
- 不等式的解集中,不包括-3的是( ) A.x<-3 B.x>-7 C.x<-1
- 热电厂用碱式硫酸铝吸收烟气中低浓度的二氧化硫.具体过程如下: (1)碱式硫酸铝溶液的制备 往Al2(SO4)3溶液中加入
- “真理是同谬误相比较而存在、相斗争而发展的!”这句话表明( ) A.真理和谬误是不可分割的 B.矛盾双方的对立统一推
- 梭伦改革的积极作用有( ) ①从根本上解决了贵族和平民的矛盾 ②大大促进了雅典农工商业的发展 ③奠
- 2010年1月4日,国务院出台《关于推进海南国际旅游岛建设发展的若干意见》,海南建设国际旅游岛正式升格为国家战略。从消费
- 将下文中的画线句子翻译成现代汉语 太祖少好飞鹰走狗,游荡无度,其叔父数言之于嵩,太祖患之。后逢叔父于路,乃阳败面喎
- Everyone knows that the Frenchmen are romantic, the Italians
- 40、下图分别表示温度、pH与酶活性的关系,下列叙述不正确的是( )A.曲线A表示酶与温度的关系,b点所对应的温度
- What was Jim doing the teacher came in? A.while



