高中 数学
已知曲线C:y2=4x,直线l过点P(﹣1,﹣2),倾斜角为30°,直线l与曲线C相交于A、B两点.
(Ⅰ)求直线l的参数方程;
(Ⅱ)求|PA|•|PB|的值.
已知向量 , 若
, 若 , 则
, 则 的值为( )
的值为( )
 , 若
, 若 , 则
, 则 的值为( )
的值为( )
A . -9
B . -1
C . 1
D . 9
已知函数  ,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围是( )
,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围是( )
 ,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围是( )
,若存在实数b,使函数g(x)=f(x)﹣b有两个零点,则实数a的取值范围是( )
A . (0,2)
B . (2,+∞)
C . (2,4)
D . (4,+∞)
设矩阵M=  的一个特征值λ对应的特征向量为
的一个特征值λ对应的特征向量为  ,求m与λ的值.
,求m与λ的值.
 的一个特征值λ对应的特征向量为
的一个特征值λ对应的特征向量为  ,求m与λ的值.
,求m与λ的值.
已知a+a﹣1= 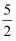 (a>1)
(a>1)
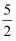 (a>1)
(a>1)
-
(1) 求下列各式的值:
(Ⅰ)a
 +a
+a  ;
;(Ⅱ)a
 +a
+a  ;
; -
(2) 已知2lg(x﹣2y)=lgx+lgy,求loga
 的值.
的值.
圆C:x2+y2=5在点(1,2)处的切线方程为( )
A . x+2y+5=0
B . 2x+y+5=0
C . 2x+y-5=0
D . x+2y-5=0
在中学生综合素质评价某个维度的测评中,分“优秀、合格、尚待改进”三个等级进行学生互评.某校高一年级有男生500人,女生400人,为了了解性别对该维度测评结果的影响,采用分层抽样方法从高一年级抽取了45名学生的测评结果,并作出频数统计表如下:
表1:男生 表2:女生
等级 | 优秀 | 合格 | 尚待改进 | 等级 | 优秀 | 合格 | 尚待改进 | |
频数 | 15 | x | 5 | 频数 | 15 | 3 | y |
(1)从表二的非优秀学生中随机选取2人交谈,求所选2人中恰有1人测评等级为合格的概率;
(2)由表中统计数据填写下边2×2列联表,并判断是否有90%的把握认为“测评结果优秀与性别有关”.

参考数据与公式:
K2= , 其中n=a+b+c+d.
, 其中n=a+b+c+d.
临界值表:
P(K2>k0) | 0.05 | 0.05 | 0.01 |
k0 | 2.706 | 3.841 | 6.635 |
在天文学中,天体的明暗程度可以用星等或亮度来描述,两颗星的星等与亮度满足 , 其中星等为
, 其中星等为 的星的亮度为
的星的亮度为 .已知甲天体的星等是
.已知甲天体的星等是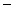 26.7,甲天体与乙天体的亮度的比值为
26.7,甲天体与乙天体的亮度的比值为 , 则乙天体的星等是( )
, 则乙天体的星等是( )
 , 其中星等为
, 其中星等为 的星的亮度为
的星的亮度为 .已知甲天体的星等是
.已知甲天体的星等是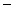 26.7,甲天体与乙天体的亮度的比值为
26.7,甲天体与乙天体的亮度的比值为 , 则乙天体的星等是( )
, 则乙天体的星等是( )
A . 1.45
B . 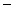 1.45
C .
1.45
C . 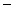 2.9
D .
2.9
D . 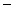 11.9
11.9
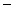 1.45
C .
1.45
C . 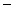 2.9
D .
2.9
D . 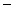 11.9
11.9
-
(1) 把
 本不同的书分给
本不同的书分给  位学生,每人至少一本,有多少种方法?
位学生,每人至少一本,有多少种方法?
-
(2) 由
 这
这  个数字组成没有重复数字的四位偶数由多少个?
个数字组成没有重复数字的四位偶数由多少个?
-
(3) 某旅行社有导游
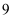 人,其中
人,其中  人只会英语,
人只会英语,  人只会日语,其余
人只会日语,其余  人既会英语,也会日语,现从中选
人既会英语,也会日语,现从中选  人,其中
人,其中  人进行英语导游,另外
人进行英语导游,另外  人进行日语导游,则不同的选择方法有多少种?
人进行日语导游,则不同的选择方法有多少种?
某位喜欢思考的同学在学习函数的性质时提出了如下两个命题:已知函数  的定义域为
的定义域为  ,
,  ,① 若当
,① 若当  时,都有
时,都有  ,则函数
,则函数  是
是  上的奇函数;② 若当
上的奇函数;② 若当  时,都有
时,都有  ,则函数
,则函数  是
是  上的增函数.下列判断正确的是( )
上的增函数.下列判断正确的是( )
 的定义域为
的定义域为  ,
,  ,① 若当
,① 若当  时,都有
时,都有  ,则函数
,则函数  是
是  上的奇函数;② 若当
上的奇函数;② 若当  时,都有
时,都有  ,则函数
,则函数  是
是  上的增函数.下列判断正确的是( )
上的增函数.下列判断正确的是( )
A . ①和②都是真命题
B . ①是真命题,②是假命题
C . ①和②都是假命题
D . ①是假命题,②是真命题
某企业开发一种产品,生产这种产品的年固定成本为3600万元,每生产x千件,需投入成本c(x)万元,c(x)=x2+10x . 若该产品每千件定价a万元,为保证生产该产品不亏损,则a的最小值为.
椭圆  与直线
与直线  交于
交于  、
、  两点,且
两点,且  ,其中
,其中  为坐标原点.
为坐标原点.
 与直线
与直线  交于
交于  、
、  两点,且
两点,且  ,其中
,其中  为坐标原点.
为坐标原点.
-
(1) 求
 的值;
的值;
-
(2) 若椭圆的离心率
 满足
满足  ,求椭圆长轴的取值范围.
,求椭圆长轴的取值范围.
方程lgx+x﹣3=0的根所在的区间是( )
A . (2,3)
B . (1,2)
C . (3,4)
D . (0,1)
若复数 满足
满足 (i为虚数单位),则
(i为虚数单位),则 ( )
( )
 满足
满足 (i为虚数单位),则
(i为虚数单位),则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若等比数列 的公比
的公比 , 且
, 且 , 又
, 又 , 那么( )
, 那么( )
 的公比
的公比 , 且
, 且 , 又
, 又 , 那么( )
, 那么( )
A .  B .
B .  C .
C .  D .
D .  与
与 的大小不能确定
的大小不能确定
 B .
B .  C .
C .  D .
D .  与
与 的大小不能确定
的大小不能确定
设![]() ,
,![]() 分别为椭圆
分别为椭圆![]()
![]() 的左右焦点,过
的左右焦点,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 的倾斜角为
的倾斜角为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() 。
。
(Ⅰ)求椭圆![]() 的焦距;
的焦距;
(Ⅱ)如果![]() ,求椭圆
,求椭圆![]() 的方程。
的方程。
已知α为第二象限角,且 sinα=![]() 求
求 的值.
的值.
已知圆![]() 的圆心坐标是
的圆心坐标是![]() ,半径长是
,半径长是![]() .若直线
.若直线![]() 与圆C相切于点
与圆C相切于点![]() ,则
,则![]() =___________,
=___________,![]() =___________.
=___________.
设扇形的周长为6,面积为2,则扇形中心角的弧度数是( ).
(A) 1 (B)4
(C)1或4 (D)![]()
函数![]() 的定义域为( )
的定义域为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- (14分,每空2分)某试剂厂用银(含杂质铜)和硝酸(含Fe3+)反应制取硝酸银,步骤如下:(1)工业上一般选用中等浓度的
- MrSmith says learning languages action,or we will
- 如图,在空间六边形(六个顶点没有任何五点共面)ABCC1D1A1中,每相邻的两边互相垂直,边长均等于a,并且AA1∥CC
- 汇率是指 A外汇在比价上的变化 B以美元表示另一国货币的价格 C以人民币的10
- 为了检测饮用水中是否会有某种细菌,配制如下培养基进行培养: 蛋白胨 10 g 乳糖 5 g 蔗糖 5 g K2HPO4
- 用36.5%的浓盐酸(密度1.2 g·cm-3)配1 mol·L-1的稀盐酸100 mL,配制过程需用到哪些仪器,且先后
- 已知正方体外接球的体积为,那么正方体的棱长等于( ) A. B. C.
- 由秦朝开始形成的中央集权政治体制,对此后近两千年中国政治与社会产生了重要影响。秦朝中央政府分管监察的是 A.丞相
- 一定质量的理想气体发生状态变化时,关于气体的三个状态参量压强、体积、温度,下 列说法正确的是 A.有一个量发生变
- The boss said to the secretary, “If you work well, you _____
- In his spare time, he often listens to music or watches TV t
- .阅读下面文字,按要求答题。(共4分) 没有蓝天的深suì,可以有白云的飘逸; ,
- 关于单摆振动中的回复力,正确的说法是:( )A.摆球的重力 B.摆球的重力沿圆弧切线方向的分力
- 根据你对元素知识的认识,请在横线上依次填写有关铝元素的5 个信息:
- . If you don’t know how to ______yourself at table in a for
- 抛物线的焦点坐标为( ) A. B. C. D.
- 维新运动期间,资产阶级维新派大量办报的主要原因是() A.清政府的重视与推动 B.国人消遣娱乐的需求 C.宣传维新思想的
- Your iPad is quite nice. Where did you buy ______? I want to
- 已知NO2和N2O4可以相互转化:N2O4(g)2NO2(g) △H <0。在恒温条件下将一定量NO2和N2O4的混合
- 中国近代在学习西方政治模式的历程中,其学习对象经历的演变是() A.英日式——美法式——俄国式 B.英日式——俄国式——



