高中 数学
在  中,角
中,角  、
、  、
、  的对边分别为
的对边分别为  、
、  、
、  ,记
,记  的面积为
的面积为  ,若
,若  ,则
,则  .
.
 中,角
中,角  、
、  、
、  的对边分别为
的对边分别为  、
、  、
、  ,记
,记  的面积为
的面积为  ,若
,若  ,则
,则  .
.
△ABC的内角A,B,C的对边分别为a,b,c,已知2cosC(acosB+bcosA)=c.
-
(1) 求角C;
-
(2) 若
 ,△ABC的面积为
,△ABC的面积为  ,求a+b的值.
,求a+b的值.
函数  图象的一个对称中心为( )
图象的一个对称中心为( )
 图象的一个对称中心为( )
图象的一个对称中心为( )
A . (  ,0)
B . (
,0)
B . (  ,0)
C . (
,0)
C . (  ,1)
D . (
,1)
D . (  ,1)
,1)
 ,0)
B . (
,0)
B . (  ,0)
C . (
,0)
C . (  ,1)
D . (
,1)
D . (  ,1)
,1)
若等边△ABC的边长为2 , 平面内一点M满足
, 平面内一点M满足 =
=
 +
+
 , 则
, 则

 =
=
 , 平面内一点M满足
, 平面内一点M满足 =
=
 +
+
 , 则
, 则

 =
=
已知点A(1,0)和圆 上一点P,动点Q满足
上一点P,动点Q满足 , 则点Q的轨迹方程为( )
, 则点Q的轨迹方程为( )
 上一点P,动点Q满足
上一点P,动点Q满足 , 则点Q的轨迹方程为( )
, 则点Q的轨迹方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
圆柱的侧面展开图是边长为2和4的矩形,则圆柱的体积是( )
A .  B .
B .  C .
C .  D .
D .  或
或 
 B .
B .  C .
C .  D .
D .  或
或 
在①  ,②
,②  ;③
;③  这三个条件中任选一个,补充在下面问题中,并做答.
这三个条件中任选一个,补充在下面问题中,并做答.
 ,②
,②  ;③
;③  这三个条件中任选一个,补充在下面问题中,并做答.
这三个条件中任选一个,补充在下面问题中,并做答. 问题:已知  的内角
的内角  的对边分别为
的对边分别为  , ▲ , 角
, ▲ , 角  的平分线交
的平分线交  于点
于点  ,求
,求  的长.
的长.
(注:如果选择多个条件分别解答,按第一个解答计分.)
已知非零向量  ,
,  满足
满足  ,且
,且  ,则
,则  与
与  的夹角为.
的夹角为.
 ,
,  满足
满足  ,且
,且  ,则
,则  与
与  的夹角为.
的夹角为.
若函数 对任意实数
对任意实数 都有
都有 , 则
, 则 的值等于( )
的值等于( )
 对任意实数
对任意实数 都有
都有 , 则
, 则 的值等于( )
的值等于( )
A . -1
B . 1
C .  D .
D . 
 D .
D . 
椭圆  (0<m<1)上存在点P使得PF1⊥PF2 , 则m的取值范围是( )
(0<m<1)上存在点P使得PF1⊥PF2 , 则m的取值范围是( )
 (0<m<1)上存在点P使得PF1⊥PF2 , 则m的取值范围是( )
(0<m<1)上存在点P使得PF1⊥PF2 , 则m的取值范围是( )
A . [  ,1)
B . (0,
,1)
B . (0,  ]
C . [
]
C . [  ,1)
D . (0,
,1)
D . (0,  ]
]
 ,1)
B . (0,
,1)
B . (0,  ]
C . [
]
C . [  ,1)
D . (0,
,1)
D . (0,  ]
]
在  中,已知
中,已知  ,
,  ,且
,且  的面积为
的面积为  ,则
,则  内切圆的面积为.
内切圆的面积为.
 中,已知
中,已知  ,
,  ,且
,且  的面积为
的面积为  ,则
,则  内切圆的面积为.
内切圆的面积为.
在锐角 中,
中, ,
,  为
为 边上的一点,且
边上的一点,且 ,
,  .
.
 中,
中, ,
,  为
为 边上的一点,且
边上的一点,且 ,
,  .
. 
-
(1) 求
 的大小;
的大小;
-
(2) 若
 , 求
, 求 .
.
对于函数(x)=  cos(2x-
cos(2x-  ),给出下列四个结论:①函数)的最小正周期为2π;②函数f(x)在[
),给出下列四个结论:①函数)的最小正周期为2π;②函数f(x)在[  ,
,  ]上的值域是[
]上的值域是[ 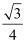 ,
,  ]:③函数f(x)在[
]:③函数f(x)在[  ]是减函数;④函数f(x)的图象关于点(-
]是减函数;④函数f(x)的图象关于点(-  ,0)对称.其中正确结论的个数是( )
,0)对称.其中正确结论的个数是( )
 cos(2x-
cos(2x-  ),给出下列四个结论:①函数)的最小正周期为2π;②函数f(x)在[
),给出下列四个结论:①函数)的最小正周期为2π;②函数f(x)在[  ,
,  ]上的值域是[
]上的值域是[ 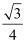 ,
,  ]:③函数f(x)在[
]:③函数f(x)在[  ]是减函数;④函数f(x)的图象关于点(-
]是减函数;④函数f(x)的图象关于点(-  ,0)对称.其中正确结论的个数是( )
,0)对称.其中正确结论的个数是( )
A . 1
B . 2
C . 3
D . 4
已知 ,
,  .
.
 ,
,  .
.
-
(1) 求
 ,
,  的值;
的值;
-
(2) 求
 的值.
的值.
在梯形  中,
中,  ,且
,且  ,
,  是等腰直角三角形,其中
是等腰直角三角形,其中  为斜边,若把
为斜边,若把  沿
沿  边折叠到
边折叠到  的位置,使平面
的位置,使平面  平面
平面  .
.
 中,
中,  ,且
,且  ,
,  是等腰直角三角形,其中
是等腰直角三角形,其中  为斜边,若把
为斜边,若把  沿
沿  边折叠到
边折叠到  的位置,使平面
的位置,使平面  平面
平面  .
. 
-
(1) 证明:
 .
.
-
(2) 若
 为棱
为棱  的中点,求二面角
的中点,求二面角  的余弦值.
的余弦值.
对于任意实数  ,符号
,符号  表示
表示  的整数部分,即
的整数部分,即  是不超过
是不超过  的最大整数,例如
的最大整数,例如  ;
;  ;则
;则  的值为( )
的值为( )
 ,符号
,符号  表示
表示  的整数部分,即
的整数部分,即  是不超过
是不超过  的最大整数,例如
的最大整数,例如  ;
;  ;则
;则  的值为( )
的值为( )
A . 42
B . 43
C . 44
D . 45
已知 , 则下列不等式正确的是( )
, 则下列不等式正确的是( )
 , 则下列不等式正确的是( )
, 则下列不等式正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在如图所示的算法框图中,若a=-8,则输出结果是( )

A.2![]() B.-2
B.-2![]() C.0 D.10
C.0 D.10
已知直线![]() 处的切线互相垂直,则
处的切线互相垂直,则![]() 的值为
的值为
A.-![]() B.
B.![]() C.
C.![]() D.-
D.-![]()
等比数列{an}满足a1=3,a1+ a3+ a5=21,则a3+ a5+ a7 =
(A)21 (B)42 (C)63 (D)84
最近更新
- 精神栖身于茅屋周国平①如果你爱读人物传记,你就会发现,许多优秀人物生前都非常贫困。最著名的印象派画家凡•高,现在他的一幅
- 关于电磁铁,下列说法正确的是:A、电破铁的磁性强弱跟通过它的电流强弱无关;B 、电进铁中电流方向改变.其磁性强弱也改变;
- 下列成语中与漫画《入市之梦》蕴涵相同哲理的是 A.仁者见仁 智者见智
- 如图所示,闭合开关S,发现电流表的示数为零,而电压表有示数,出现这种故障的原因可能是()A.灯泡L短路 B. 开关
- -Do you know________? -At two O’clock.We still have enoug
- 减数分裂第一次分裂(MI)过程中不会出现的是( ) A.同源染色体配对(联会) B.四分体中非姐
- 公有制为主体,多种所有制经济共同发展是我国社会主义初级阶段的基本经济制度。对“公有制为主体”理解正确的是 A.公有制在各
- 金属镍有广泛的用途。粗镍中含有少量Fe、Zn、Cu、Pt等杂质,可用电解法制备高纯度的镍,下列叙述正确的是(已知:氧化性
- 下列历史人物中,其历史评价与历史价值不同的是 A.华盛顿 B.罗伯斯庇尔 C
- 等物质的量的钠、镁、铝三种金属分别与足量的盐酸反应。 (1)产生的氢气的质量之比是多少? (2)生成三种盐的物质的量之比
- 下列运算正确的是() A. a3﹣a2=a B. (a2)3=a5 C. a4•a=a5
- 有关愈伤组织的说法错误的是( ) A. 愈伤组织进行异养生活,有氧呼吸 B. 愈伤组织细胞再诱导后才进行分化 C.
- 某工业混合液中含有的组分仅可能是乙醚(C4H10O)、乙醇(C2H6O)和水。经分析,液体中各原子数之比为N(C):N(
- 如图N27,要使输出值y大于100,则输入的最小正整数x是________.图N27
- 温家宝总理说,通货膨胀就像一只老虎,如果放出来就很难再关进去。导致恶性通货膨胀的经济原因一般是
- 在紫色洋葱的表皮细胞中含有RNA的结构有() ①细胞质基质 ②线粒体基质 ③叶绿体基质 ④核糖体 ⑤中心体 A.①②③⑤
- 目前,开发海洋资源,如采油、捕鱼、航运等,主要在海底的哪种地形进行?( )A、① B、②
- 右面漫画中的“大饼”代表中国,而围着大饼的是手持匕首的列强,他们迫不及待地对着“大饼”下刀,唯恐落于人后,大饼的主人则只
- 19.仿照下面句式,写一个结构相似、复句形式相同的句子。 只有波涛澎湃的大海,才能创造出沙滩的光洁和柔软;而平静的
- 在一次实验课上,老师要求同学们用试管取一些稀盐酸,下列四位同学的操作合理的是()A. 向试管内注入1mL稀盐酸 B. 向



