高中 数学
将函数  的图象向左平移
的图象向左平移  个单位后得到函数
个单位后得到函数  的图象,则
的图象,则 
 的图象向左平移
的图象向左平移  个单位后得到函数
个单位后得到函数  的图象,则
的图象,则 
A . 为奇函数,在  上单调递減
B . 最大值为1,图象关于直线
上单调递減
B . 最大值为1,图象关于直线  对称
C . 周期为
对称
C . 周期为  ,图象关于点
,图象关于点  对称
D . 为偶函数,在
对称
D . 为偶函数,在  上单调递增
上单调递增
 上单调递減
B . 最大值为1,图象关于直线
上单调递減
B . 最大值为1,图象关于直线  对称
C . 周期为
对称
C . 周期为  ,图象关于点
,图象关于点  对称
D . 为偶函数,在
对称
D . 为偶函数,在  上单调递增
上单调递增
若直线l与直线y=1,x=7分别交于P,Q,且线段PQ的中点坐标为(1,-1),则直线l的斜率为( )
A .  B . -
B . -  C . 3
D . -3
C . 3
D . -3
 B . -
B . -  C . 3
D . -3
C . 3
D . -3
设集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A . 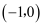 B .
B .  C .
C .  D .
D . 
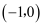 B .
B .  C .
C .  D .
D . 
若C是线段AB的中点,则  =( )
=( )
 =( )
=( )
A .  B .
B .  C .
C .  D . 以上均不正确
D . 以上均不正确
 B .
B .  C .
C .  D . 以上均不正确
D . 以上均不正确
已知函数  .
.
 .
.
-
(1) 求
 的最大值;
的最大值;
-
(2) 若
 ,分析
,分析  在
在  上的单调性.
上的单调性.
当生物死亡后,其体内原有的碳14的含量大约每经过5730年衰减为原来的一半,这个时间称为“半衰期”.当死亡生物体内的碳14含量不足死亡前的千分之一时,用一般的放射性探测器就测不到了.若某死亡生物体内的碳14用该放射性探测器测不到,则它经过的“半衰期”个数至少是( )
A . 8
B . 9
C . 10
D . 11
已知函数  ,且
,且  .
.
 ,且
,且  .
.
-
(1) 求m的值;
-
(2) 证明
 的奇偶性;
的奇偶性;
-
(3) 若不等式
 在
在  上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
若x3=a0+a1(x﹣2)+a2(x﹣2)2+a3(x﹣2)3 , 则a2的值为( )
A . 12
B . 9
C . 6
D . 3
函数  定义域为.
定义域为.
 定义域为.
定义域为.
已知集合M={x|lg(x﹣2)≤0},N={x|﹣1≤x≤3},则M∪N=( )
A . {x|x≤3}
B . {x|2<x<3}
C . {x|﹣1≤x≤3}
D . R
设  ,
,  是两条不同的直线,
是两条不同的直线,  ,
,  是两个不同的平面,则
是两个不同的平面,则  的一个充分不必要条件是( )
的一个充分不必要条件是( )
 ,
,  是两条不同的直线,
是两条不同的直线,  ,
,  是两个不同的平面,则
是两个不同的平面,则  的一个充分不必要条件是( )
的一个充分不必要条件是( )
A .  ,
,  ,
,  B .
B .  ,
,  ,
,  C .
C .  ,
,  ,
,  D .
D .  ,
,  ,
, 
 ,
,  ,
,  B .
B .  ,
,  ,
,  C .
C .  ,
,  ,
,  D .
D .  ,
,  ,
, 
在复平面内,复数z=i(1+2i)对应的点位于( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
命题“所有能被2整除的数都是偶数”的否定是( )
A . 所有不能被2整除的整数都是偶数
B . 所有能被2整除的整数都不是偶数
C . 存在一个不能被2整除的整数是偶数
D . 存在一个能被2整除的整数不是偶数
已知函数f(x)=2sin(2ωx+  )+1(其中0<ω<1),若点(﹣
)+1(其中0<ω<1),若点(﹣  ,1)是函数f(x)图象的一个对称中心,
,1)是函数f(x)图象的一个对称中心,
 )+1(其中0<ω<1),若点(﹣
)+1(其中0<ω<1),若点(﹣  ,1)是函数f(x)图象的一个对称中心,
,1)是函数f(x)图象的一个对称中心, 
-
(1) 试求ω的值;
-
(2) 先列表,再作出函数y=f(x﹣
 )在区间[﹣π,π]上的图象.
)在区间[﹣π,π]上的图象.
在△ABC中,角A、B、C所对的边为a、b、c,若a、b、c成等比数列,且  ,则
,则  的值是.
的值是.
 ,则
,则  的值是.
的值是.
 的内角
的内角  、
、  、
、  的对边分别为
的对边分别为  、
、  、
、  ,已知
,已知  .
.
-
(1) 求
 ;
;
-
(2) 若等差数列
 的公差不为0,且
的公差不为0,且  ,
,  、
、  、
、  成等比数列,求数列
成等比数列,求数列  前
前  项和
项和  .
.
已知圆心为C的圆经过点A(0,—6),B(1,—5),且圆心在直线![]() 上,求圆心为C的圆的标准方程。
上,求圆心为C的圆的标准方程。
若函数 是
是![]() 上的增函数,则实数
上的增函数,则实数![]() 的范围为( )
的范围为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知![]() 是偶函数,定义域为
是偶函数,定义域为![]() ,则
,则![]() = ( )
= ( )
A. ![]() B. 1 C.0
B. 1 C.0 ![]() D.
D.![]()
在平面直角坐标系![]() 中,已知过点
中,已知过点![]() 的直线
的直线![]() 与圆
与圆![]() 相切,且与直线
相切,且与直线![]() 垂直,则实数
垂直,则实数![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 将一严重锈蚀而部分变成铜绿的铜块研磨成粉末,在空气中充分灼烧成CuO,发现固体质量在灼烧前后保持不变。灼烧前粉末中铜的
- He is up to his old t_______. Don't trust him.
- (07年石景山一模文)以原点为圆心,且截直线所得弦长为8的圆的方程是 ( )
- 乙酸橙花酯是一种食用香料,结构如图所示。下列关于该有机物的说法有如下几种: ①该有机物有一种同分异构体属于酚类; ②该有
- 动物卵细胞与精子形成不同之处是 A.次级卵母细胞进行的是普通有丝分裂 B.一个卵原细胞只形成一
- 东亚季风气候最显著的原因是( ) A.地形类型复杂多样 B.亚欧大陆与太平洋的热力性质差异
- 首次提出生物学这个科学名词的是( )A.拉马克 B.林奈 C.达尔文
- 已知向量. (1)求的最大值及取最大值时的取值集合; (2)在△中,是角的对边若且, 求△的周长的取值范围.
- 用惰性电极电解下列溶液,一段时间后,再加入一定质量的另一种物质(括号内),溶液能与原来溶液完全一样的是.A. CuCl
- 要了解阿拉伯帝国丰富的社会生活,首先应查阅 A.《荷马史诗》
- 人长时间运动后,产生口渴感觉的原因是 ( ) A.血浆CO
- 下列叙述中,不正确的是 A.某特定反应的平衡常数仅是温度的函数 B.化学平衡发生移动,平衡常数必发生变化
- 下列计算正确的是( ) A. B. C. D.
- 匹兹堡成为美国钢铁工业中心的因素是 ( ) ①附近有优质煤炭 ②美国东北部工业的崛起 ③宾西法尼亚运河的开通
- I heard you have vacant position for a secretary. I’
- 试用一句话概括下面一段话的主要内容(不超过30个字) 当我们与身边的朋友相处或者与远在天边的朋友通信时,我们往往会从
- 为了经久耐用,在灯泡中可填充的气体是 A.氧气 B.氮气 C.一氧化碳 D.二氧化碳
- ------- Would you please _________ me of the meeting tomorro
- 如图,以□ABCD对角线的交点为坐标原点,以平行于AD边的直线为x轴,建立平面直角坐标系.若点D的坐标为(3,2),则点
- 2010年11月3日,我国发射的“嫦娥二号”卫星,开始在距月球表面约100 km的圆轨道上进行长期的环月科学探测试验;2



