高中 数学
现有三个条件:
①对任意的  都有
都有  ;
;
②不等式  的解集为
的解集为  ;
;
③函数  的图象过点
的图象过点 
请你在上述三个条件中任选两个补充到下面的问题中,并求解(请将所选条件的序号填写在答题纸指定位置):
已知二次函数  ,且满足 (填所选条件的序号).
,且满足 (填所选条件的序号).
-
(1) 求函数
 的解析式;
的解析式;
-
(2) 设
 ,若不等式
,若不等式  在
在  上恒成立,求实数
上恒成立,求实数  的取值范围.
的取值范围.
已知 , 函数y=f(x+φ)(|φ|≤
, 函数y=f(x+φ)(|φ|≤ )的图象关于直线x=0对称,则φ的值为
)的图象关于直线x=0对称,则φ的值为
 , 函数y=f(x+φ)(|φ|≤
, 函数y=f(x+φ)(|φ|≤ )的图象关于直线x=0对称,则φ的值为
)的图象关于直线x=0对称,则φ的值为
已知关于x的二次函数f(x)=ax2﹣4bx+1.
(Ⅰ)设集合A={﹣1,1,2,3,4,5}和B={﹣2,﹣1,1,2,3,4},分别从集合A,B中随机取一个数作为a和b,求函数y=f(x)在区间[1,+∞)上是增函数的概率.
(Ⅱ)设点(a,b)是区域  内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
内的随机点,求函数f(x)在区间[1,+∞)上是增函数的概率.
在  中,
中,  ,
,  ,
,  ,则
,则  ( )
( )
 中,
中,  ,
,  ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 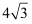
 B .
B .  C .
C .  D .
D . 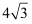
曲线y=ex+2在P(0,3)处的切线方程是.
在  中,已知
中,已知  ,
,  ,
,  ,则
,则 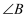 的度数是
的度数是 

 中,已知
中,已知  ,
,  ,
,  ,则
,则 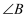 的度数是
的度数是 

A .  B .
B .  C .
C .  D .
D .  或
或 
 B .
B .  C .
C .  D .
D .  或
或 
已知直线  与圆
与圆  相交于
相交于  两点.
两点.
 与圆
与圆  相交于
相交于  两点.
两点.
-
(1) 求
 ;
;
-
(2) 若
 为圆
为圆  上的动点,求
上的动点,求  的取值范围.
的取值范围.
将5位同学分别保送到北京大学,上海交通大学,中山大学这3所大学就读,每所大学至少保送1人,则不同的保送方法共有( )
A . 150种
B . 180种
C . 240种
D . 540种
已知函数 .
.
 .
.
-
(1) 求函数
 的最小值;
的最小值;
-
(2) 求证:
 .
.
已知函数  的定义域为R,则实数a的取值范围.
的定义域为R,则实数a的取值范围.
 的定义域为R,则实数a的取值范围.
的定义域为R,则实数a的取值范围.
下列函数中与y=x为同一函数的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若“∀x∈[ 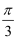 ,
,  ],cosx≤m”是真命题,则实数m的最小值为( )
],cosx≤m”是真命题,则实数m的最小值为( )
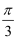 ,
,  ],cosx≤m”是真命题,则实数m的最小值为( )
],cosx≤m”是真命题,则实数m的最小值为( )
A . ﹣  B . ﹣
B . ﹣  C .
C .  D .
D . 
 B . ﹣
B . ﹣  C .
C .  D .
D . 
在如图所示的程序框图中,输入f0(x)=cosx,则输出的是( )
A . sinx
B . -sinx
C . cosx
D . -cosx
已知函数f(x)的图象是连续不断的,有如下x,f(x)的对应值表:
x | 1 | 2 | 3 | 4 | 5 | 6 |
f(x) | 123.56 | 21.45 | ﹣7.82 | 11.57 | ﹣53.76 | ﹣126.49 |
函数f(x)在区间[1,6]上的零点至少有( )
A . 2个
B . 3个
C . 4个
D . 5个
已知全集为U,集合 ,
,  , 则图中阴影部分表示的集合为( )
, 则图中阴影部分表示的集合为( )
 ,
,  , 则图中阴影部分表示的集合为( )
, 则图中阴影部分表示的集合为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在直角坐标系中,参数方程为 (t为参数)的直线l被以原点为极点,x轴的正半轴为极轴,极坐标方程为ρ=2cos θ的曲线C所截,求截得的弦长.
(t为参数)的直线l被以原点为极点,x轴的正半轴为极轴,极坐标方程为ρ=2cos θ的曲线C所截,求截得的弦长.
已知直线l过点(1,1),过点P(-1,3)作直线m⊥l,垂足为M,则点M到点Q(2,4)距离的取值范围为 .
若![]() =
=![]() ,则tan 2α=
,则tan 2α=
A.-![]() B.
B.![]() C.-
C.-![]() D.
D.![]()
等差数列{an}中,a2=4,a4+a7=15.
(1)求数列{an}的通项公式;
(2)设bn=2an-2+n,求b1+b2+b3+…+b10的值.
已知数列{a }的前n项和为S
}的前n项和为S ,且S
,且S =2a
=2a -1,则数列{
-1,则数列{ }的前6项和为____.
}的前6项和为____.
最近更新
- ..----Do you regret not having gone abroad? ----Not at all.
- 下图为具有6条染色体的某生物细胞进行有丝分裂过程的几个阶段,请分析回答: (1)根据丙图的特有变化特征,可以判断该图表
- 下列表述不正确的是() A.人造刚玉熔点很高,可用作高级耐火材料,主要成分是Al2O3 B.在医疗上碳酸氢钠可用于治疗
- 如图所示是两个点电荷形成的静电场的电场线,图中P、Q两点的电场强度的大小分别为EP和EQ,电势分别为jP和jQ,则下列正
- 3.填入下面文段空白处的词语,最恰当的一组是 手机里存储的数据都是由0和1排列而成的二进制数字组成的,它们__①__会占
- △ABC中,a=2,b=3,c=4,则△ABC的形状是: A.一定是锐角三角形; B 一定是直角三角形C 一定是钝角三角
- 比较铜和银的金属活动性强弱,可选用的药品是( ) A.稀盐酸 B.稀硫酸 C.硫酸锌溶液 D.硝酸汞
- 某同学在研究性学习中记录了一些与地球、月球有关的数据资料如表中所示,利用这些数据来计算地球表面与月球表面之间的距离s,则
- 读下图,完成下列问题。(1)世界上最早出现城市的地区是:A ,B ,C ,D
- 29.下列细胞中,含高尔基体和内质网较多的是( ) A.神经细胞 B.唾液腺细胞 C.汗
- 根据汉语意思完成句子,每空一词。 1.在这里写下你的电话号码和电子邮件地址。 ________ ________ you
- 好多农俗、谚语充满古代劳动人民的智慧,像“东虹轰隆西虹雨”“云彩向东一阵风,云彩向北一阵黑”“
- 图4是某城镇用地布局规划方案示意图。读图回答5-6题。5.该方案突出优点是 A.规划的居住区远离铁路 B. 规划的居住
- 郑和下西洋与欧洲的新航路开辟活动产生了不同结果的根源在于 ( ) A.目的不同
- 不是每一朵花都能结出果实,能结出果实的花一定( ) ①长有雌蕊和雄蕊 ②长有雌蕊 ③经历了自花传粉 ④经
- 固定的气缸内由活塞封闭着一定量的理想气体,活塞在拉力F作用下缓慢地向右移动,如图5-13所示.假设气缸壁和活塞都是不导热
- 水平固定放置的足够长的U形金属导轨处于竖直向上的匀强磁场中,在导轨上放着金属棒ab,开始时ab棒以水平初速度v0向右运动
- 打捞韩国“岁月号”沉船是在水下作业,潜水员需要呼吸富氧空气。富氧空气中氧气含量高于普通空气中的含量,富氧空气中氧气与其他
- 下列各组微粒具有相同质子数和电子数的是 ( ) A.OH—和NH4+ B.
- 植物可以进行无土栽培的原因是( ) A.植物吸收的并不是土壤中的无机盐 B.植物的根从土壤中吸收的仅是水分和无机盐



