高中 数学
tan75°=( )
A .  B .
B .  C .
C .  D . tan25°tan35°tan85°
D . tan25°tan35°tan85°
 B .
B .  C .
C .  D . tan25°tan35°tan85°
D . tan25°tan35°tan85°
将集合M={1,2,3,…15}表示为它的5个三元子集(三元集:含三个元素的集合)的并集,并且这些三元子集的元素之和都相等,则每个三元集的元素之和为;请写出满足上述条件的集合M的5个三元子集.(只写出一组)
“  ”是“
”是“  ”的条件(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”).
”的条件(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”).
 ”是“
”是“  ”的条件(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”).
”的条件(填“充分不必要”、“必要不充分”、“充要”或“既不充分也不必要”).
已知函数f(x)=2x﹣2,则函数y=|f(x)|的图象可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
阅读如图所示的程序框图,运行相应的程序,输出的结果i=.

已知  是定义在
是定义在  上的偶函数,当
上的偶函数,当 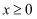 时,
时,  .
.
 是定义在
是定义在  上的偶函数,当
上的偶函数,当 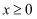 时,
时,  .
.
-
(1) 当
 时,求函数
时,求函数  的解析式;
的解析式;
-
(2) 解关于
 的不等式
的不等式  .
.
已知圆锥的底面直径为2,侧面展开图为半圆,则圆锥的体积为.
若  ,
,  ,则
,则  的最小值为.
的最小值为.
 ,
,  ,则
,则  的最小值为.
的最小值为.
已知点A、B、C为椭圆  :
:  上的三点,
上的三点,  为坐标原点,当
为坐标原点,当  时,称
时,称  为“稳定三角形”,则这样的“稳定三角形”( )
为“稳定三角形”,则这样的“稳定三角形”( )
 :
:  上的三点,
上的三点,  为坐标原点,当
为坐标原点,当  时,称
时,称  为“稳定三角形”,则这样的“稳定三角形”( )
为“稳定三角形”,则这样的“稳定三角形”( )
A . 不存在
B . 存在有限个
C . 有无数个但面积不为定值
D . 有无数个且面积为定值
在我国古代数学著作《详解九章算法》中,记载着如图所示的一张数表,表中除1以外的每一个数都等于它肩上两个数之和,如:6=3+3则这个表格中第8行第6个数是( )

A . 21
B . 28
C . 35
D . 56
某地区今年1月,2月,3月,4月,5月患某种传染病的人数分别是52,61,68,74,78.若用下列四个函数模型预测以后各月的患该种传染病的人数,哪个最不合理( )
A . f(x)=kx+h
B . f(x)=ax2+bx+c
C . f(x)=pqx+r
D . f(x)=mlnx+n
已知幂函数f(x)=x  (m∈N*)的图象经过点
(m∈N*)的图象经过点  .
.
 (m∈N*)的图象经过点
(m∈N*)的图象经过点  .
.
-
(1) 试求m的值并写出该幂函数的解析式;
-
(2) 试求满足f(1+a)>f(3﹣
 )的实数a的取值范围.
)的实数a的取值范围.
如图,  是圆
是圆  的直径,
的直径,  垂直圆
垂直圆  所在的平面,
所在的平面,  是圆
是圆  上的点.
上的点.
 是圆
是圆  的直径,
的直径,  垂直圆
垂直圆  所在的平面,
所在的平面,  是圆
是圆  上的点.
上的点.
-
(1) 求证:
 平面
平面  ;
;
-
(2) 设
 为
为  的中点,
的中点,  为
为  的重心,求证:
的重心,求证:  平面
平面  .
.
如图,边长为2的正方形中有一阴影区域,在正方形中随机撒一粒豆子,它落在阴影区域内的概率为![]() .则阴影区域的面积约为 ( )
.则阴影区域的面积约为 ( )

A.![]() B.
B.![]() C.
C.![]() D.无法计算
D.无法计算
连续两次掷一颗质地均匀的骰子(一种各面上分别标有1,2,3,4,5,6个点的正方体玩具),记出现向上的点数分别为![]() ,设向量
,设向量![]() ,
,![]() ,则
,则![]() 与
与![]() 的夹角为锐角的概率是 ▲ .
的夹角为锐角的概率是 ▲ .
![]()
.叙述并证明直线与平面垂直的判定定理.
已知幂函数的图象过点(2,16)和(![]()
![]() ,m),则m= .
,m),则m= .
如图,椭圆![]() 的左、右顶点分别为
的左、右顶点分别为![]() 、
、![]() ,双曲线
,双曲线![]() 以
以![]() 、
、![]() 为顶点,焦距为
为顶点,焦距为![]() .点
.点![]() 是
是![]() 上在第一象限内的动点,直线
上在第一象限内的动点,直线![]() 与椭圆相交于另一点
与椭圆相交于另一点![]() ,线段
,线段![]() 的中点为
的中点为![]() ,记直线
,记直线![]() 的斜率为
的斜率为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求双曲线![]() 的方程;
的方程;
(2)求点![]() 的纵坐标
的纵坐标![]() 的取值范围;
的取值范围;
(3)是否存在定直线![]() ,使得直线
,使得直线![]() 与直线
与直线![]() 关于直线
关于直线![]() 对称?若存在,求直线
对称?若存在,求直线![]() 的方程;若不存在,请说明理由.
的方程;若不存在,请说明理由.

如图,在平行四边形![]() 中,已知
中,已知![]() ,
, ![]() ,
,![]() ,
,![]() , 则
, 则![]() 的值是 .
的值是 .
 |
最近更新
- 下图是中国产业信息网提供的我国芯片供求情况(单位:10亿美元):注:目前我国芯片市场规模占全球的60%,但自给率尚不
- Tomis a top student in our class , How itbe that he
- 2003 年“神五”圆了中国人的飞天梦,2 。。5 年“神六”首次实现了两人五天的太空飞行并开展了太空科学实验,2008
- 最后一课(节选)我一纵身跨过板凳就坐下。我的心稍微平静了一点儿,我才注意到,我们的老师今天穿上了他那件挺漂亮的绿色礼服,
- 植物的呼吸作用与光合作用分别在植物细胞的( )中进行。 A. 叶绿体细胞核 B. 液泡、细胞核 C.
- 阅读下面短文,根据短文内容回答下列各题。 (A)Helen Keller was born in 1880 in USA
- 辛亥革命是中国近代历史进程中的一个重要里程碑。下列有关它的表述,不正确的是 A、它结束了两千多年的封建帝制
- —Excuseme,_____ hat is that? —Oh,it belongs to ___
- II 语言知识及应用(共两节,满分35分) 第一节 完形填空(共10小题;每小题2分,满分20分) 阅读下面的短文,
- 2012年6月16日,“神舟九号”飞船在酒泉卫星发射中心发射升空后准确进入预定轨道。“神舟九号”搭载三名航天员进入太空,
- .若2,3,x, 5,这四个数的平均数是4,则x=( )A. 4 B. 5
- 柑橘、柠檬芳香油的制备通常使用压榨法而不是水中蒸馏法,这是因为() ①水中蒸馏会导致原料焦糊 ②柑橘、柠檬芳香油易溶于水
- 如图所示,作用于坐标原点O的三个力平衡,已知三个力均位于xOy平面内,其中力F1的大小不变,方向沿y轴负方向;力F2的大
- 对以下三幅中外美术作品(图10~12)的表述,完全正确的一组是( ) A.作者:宋朝 法国
- CO、H2、CH30H均是清洁能源,一定条件下存在如下转化:CO(g)+2H2(g)CH30H(g) △H=-105kJ
- 用显微镜观察标本时,目镜有5X、10X两种,物镜有10X和40X两种,下列组合中视野中观察到的细胞数目最多的是
- 下列除杂方案正确的是 序号 物质 (括号内为杂质)
- One of the easiest ways to keep healthyis to do jogging. “
- 2011•金华十校期末 网络用语:“人生就像牙缸,你可以把它看成杯(悲)具,也可以看成洗(喜)具”这说明 ①体现了
- 选出下面各项中字音有误的一项:A体己tī 轧钢zhá 颤栗zhàn 稽首qǐB片子piān吞咽yàn 轧帐gá称赞chē



