高中 数学
 的内角A、B、C的对边分别为a、b、c.已知
的内角A、B、C的对边分别为a、b、c.已知  ,
,  ,
,  ,则角
,则角 
已知向量  ,
,  ,
,  .
.
 ,
,  ,
,  .
.(Ⅰ)求  的值;
的值;
(Ⅱ)若  ,
,  ,且
,且  ,求
,求  的值.
的值.
已知△ABC的三边长a,b,c依次成等差数列,a2+b2+c2=21,则b的取值范围是.
设集合  ,则
,则  为( )
为( )
 ,则
,则  为( )
为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若三个正数  ,
,  ,
,  成等比数列,其中
成等比数列,其中  ,
,  ,则
,则  .
.
 ,
,  ,
,  成等比数列,其中
成等比数列,其中  ,
,  ,则
,则  .
.
已知椭圆C: ,
,  、
、 为椭圆的左、右焦点,焦距为2
为椭圆的左、右焦点,焦距为2 , P(
, P( -
- )为椭圆上一点.
)为椭圆上一点.
 ,
,  、
、 为椭圆的左、右焦点,焦距为2
为椭圆的左、右焦点,焦距为2 , P(
, P( -
- )为椭圆上一点.
)为椭圆上一点.
-
(1) 求椭圆C的标准方程;
-
(2) 已知过点(0,-
 )的直线l与C交于A,B两点;线段AB的中点为M,在
)的直线l与C交于A,B两点;线段AB的中点为M,在 轴上是否存在定点N,使得
轴上是否存在定点N,使得 恒成立?若存在,求出点N的坐标;若不存在,请说明理由.
恒成立?若存在,求出点N的坐标;若不存在,请说明理由.
若10x=3,10y=4,求10x﹣2y的值.
 的展开式中,
的展开式中, 项的系数为( )
项的系数为( )
A . 36
B . 56
C . 84
D . 90
函数  的部分图象大致为( )
的部分图象大致为( )
 的部分图象大致为( )
的部分图象大致为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
用反证法证明:对任意的x∈R,关于关于x的方程x2﹣5x+m=0与2x2+x+6﹣m=0至少有一个方程有实根.
在三棱柱  中,
中,  是等边三角形,
是等边三角形,  平面
平面  ,则异面直线
,则异面直线  和
和  所成角的正弦值为( )
所成角的正弦值为( )
 中,
中,  是等边三角形,
是等边三角形,  平面
平面  ,则异面直线
,则异面直线  和
和  所成角的正弦值为( )
所成角的正弦值为( ) 
A . 1
B .  C .
C . 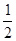 D .
D . 
已知  、
、  为锐角,
为锐角,  ,
,  ,则
,则 
 、
、  为锐角,
为锐角,  ,
,  ,则
,则 
算盘是中国传统的计算工具.东汉徐岳所撰的《数术记遗》中记载:“珠算,控带四时,经纬三才.”用如图所示的算盘表示数时,约定每档中有两粒算珠(上珠中最上面的一粒和下珠中最下面的一粒)不使用. 如果一个数在算盘上能够用个位、十位和百位这三档中的2粒算珠表示,则这个数能够被3整除的概率是( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设点 是椭圆
是椭圆 :
: 上的动点,点
上的动点,点 是圆
是圆 :
: 上的动点,且直线
上的动点,且直线 与圆
与圆 相切,则
相切,则 的最小值是.
的最小值是.
 是椭圆
是椭圆 :
: 上的动点,点
上的动点,点 是圆
是圆 :
: 上的动点,且直线
上的动点,且直线 与圆
与圆 相切,则
相切,则 的最小值是.
的最小值是.
已知函数 ,
,  .
.
 ,
,  .
.
-
(1) 若函数
 在区间
在区间 内单调递增,求实数a的取值范围;
内单调递增,求实数a的取值范围;
-
(2) 若
 , 且
, 且 , 求证:
, 求证: .
.
设  是两平面,
是两平面,  是两直线.下列说法正确的个数是( )
是两直线.下列说法正确的个数是( )
 是两平面,
是两平面,  是两直线.下列说法正确的个数是( )
是两直线.下列说法正确的个数是( ) ①若  ,则
,则  ②若
②若  ,则
,则 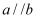
③若  ,则
,则  ④若
④若  ,则
,则 
A . 1
B . 2
C . 3
D . 4
已知向量  ,则向量
,则向量  的单位向量
的单位向量  .
.
 ,则向量
,则向量  的单位向量
的单位向量  .
.
随着人们经济收入的不断增长,个人购买家庭轿车已不再是一种时尚.车的使用费用,尤其是随着使用年限的增多,所支出的费用到底会增长多少,一直是购车一族非常关心的问题.某汽车销售公司做了一次抽样调查,并统计得出某款车的使用年限  (单位:年)与所支出的总费用
(单位:年)与所支出的总费用  (单位:万元)有如下的数据资料:
(单位:万元)有如下的数据资料:
 (单位:年)与所支出的总费用
(单位:年)与所支出的总费用  (单位:万元)有如下的数据资料:
(单位:万元)有如下的数据资料:使用年限 | 2 | 3 | 4 | 5 | 6 |
总费用 | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
若由资料知  对
对  呈线性相关关系.
呈线性相关关系.
-
(1) 试求线性回归方程
 =
= 
 +
+  的回归系数
的回归系数  ,
,  ;
;
-
(2) 当使用年限为
 年时,估计车的使用总费用.
年时,估计车的使用总费用.
已知函数 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
 是定义在
是定义在 上的奇函数,且
上的奇函数,且 .
.
-
(1) 求
 ,
,  的值;
的值;
-
(2) 判断
 在
在 上的单调性,并用定义证明.
上的单调性,并用定义证明.
已知a>0,函数f(x)=ax-bx2.
(1)当b>0时,若对任意x∈R都有f(x)≤1,证明a≤2![]() ;
;
(2)当b>1时,证明对任意x∈[0,1],|f(x)|≤1的充要条件是b-1≤a≤2![]() .
.
最近更新
- 小明是热爱生活、爱好化学的学生,下列是他平时的部分观察、记录、分析、总结,其中不科学的是 A.金刚石、石墨物理性质差异很
- .二次函数y=ax2+bx+c的图象如图所示,下列结论: ①4ac<b2;②a+c>b;③2a+b>0. 其中正确的有(
- 下列化学用语正确的是A.乙烯的结构简式可表示为CH2CH2 B.乙醇的分子式:CH3CH2OH C. 乙酸的
- 已知双曲线与椭圆的焦点重合,它们的离心率之和为,则双曲线的渐近线方程为 A、 B、C、 D、
- 2016年诺贝尔化学奖由法国斯特拉斯堡大学的让皮埃尔•索瓦日、美国西北大学的弗雷泽•斯托达特和荷兰格罗宁根大学的伯纳德•
- 求证: +>2+(必须用分析法,否则记零分)
- 豚鼠的黑毛对白毛是显性,一饲养员让两只杂合豚鼠杂交,其一胎所产生的小豚鼠可能是 A.只有黑色或只有白色
- 阅读下列唐诗,完成小题。(4分)题破山寺后禅院(唐)常建清晨入古寺,初日照高林。竹径通幽处,禅房花木深。山光悦鸟性,潭影
- 如图,长方形ABCD中,AB=6,BC=8,点P从A出发沿A→B→C→D的路线移动,设点P移动的路线为x,△PAD的面积
- (本题满分7分)在对人们休闲方式的一次调查中,共调查120人,其中女性70人、男性50人,女性中有40人主要的休闲方式是
- 下列各图是初中化学常见的几个实验操作,其中错误的是[ ]
- 主族元素A、B、C、D、E的原子序数都小于18,A与D同主族,B与C在同一周期,A、D原子的最外层电子数都是1,C原子最
- 一只不透明的袋子中装有4个黑球、2个白球,每个球除颜色外都相同,从中任意摸出3个球,下列事件为必然事件的是( )
- 右图是实验室常用的两套气体发生装置 ① 写出编号仪器的名称:a (1) ,如将B装置中仪器b如果换成分液漏斗的目的是
- 对洋务运动认识不准确的是( ) A、洋务运动是采用西方的政治制度 B、维护清朝统治是其根本目
- 2009年2月12日,三鹿集团被正式宣告破产。这是自1986年第一部《企业破产法》颁布实施以来,中国因产品质量问题而破产
- 读冀北某地等高线地形图(图4),回答7-8题。图4 7.为把铝土矿石运到火车站,计划修一条公路,合理的选线是a、b、c、
- 如图14所示中的4×4的正方形网格中,∠1+∠2+∠3+∠4+∠5+∠6+ ∠7=( ) A.245° B.3
- (宁波市)5.名著阅读。(4分) (1)下面是丰子恺先生为《朝花夕拾》画的三幅插图。根据画意和文字提示,任选两幅写出相关
- 若与互为相反数,求的值为_________.



