高中 数学
在  中,角
中,角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  ,且
,且  边上的高为
边上的高为  ,则
,则  的最大值是( )
的最大值是( )
 中,角
中,角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  ,且
,且  边上的高为
边上的高为  ,则
,则  的最大值是( )
的最大值是( )
A . 8
B . 6
C . 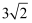 D . 4
D . 4
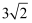 D . 4
D . 4
已知tanα=3,则 的值
的值
 的值
的值
下列函数中在定义域上既是奇函数又是增函数的为( )
A . y=x+1
B . y=-x2
C . y=x3
D . 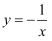
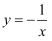
已知函数  ,若关于
,若关于  的方程
的方程  有唯一实数根,则实数
有唯一实数根,则实数  的取值范围是( )
的取值范围是( )
 ,若关于
,若关于  的方程
的方程  有唯一实数根,则实数
有唯一实数根,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在平面直角坐标系  中,已知椭圆
中,已知椭圆  ,过点
,过点  作直线l与椭圆交于A,B两点.
作直线l与椭圆交于A,B两点.
 中,已知椭圆
中,已知椭圆  ,过点
,过点  作直线l与椭圆交于A,B两点.
作直线l与椭圆交于A,B两点.
-
(1) 若
 是直线l的一个法向量,求直线l的标准方程;
是直线l的一个法向量,求直线l的标准方程;
-
(2) 若
 的面积为
的面积为  ,求直线l的方程;
,求直线l的方程;
-
(3) 在线段
 上取点Q,使得
上取点Q,使得  ,求证:点Q在一条定直线上.
,求证:点Q在一条定直线上.
已知圆 与
与 .
.
 与
与 .
.
-
(1) 过点
 作直线
作直线 与圆
与圆 相切,求
相切,求 的方程;
的方程;
-
(2) 若圆
 与圆
与圆 相交于
相交于 、
、 两点,求
两点,求 的长.
的长.
一机械制造加工厂的某条生产线在设备正常运行的情况下,生产的零件尺寸z(单位: )服从正态分布
)服从正态分布 , 且
, 且 , 则
, 则 ( )
( )
 )服从正态分布
)服从正态分布 , 且
, 且 , 则
, 则 ( )
( )
A . 0.1
B . 0.04
C . 0.05
D . 0.06
已知  为单调递增的等差数列,
为单调递增的等差数列,  ,
,  ,设数列
,设数列  满足
满足  ,
,  .
.
 为单调递增的等差数列,
为单调递增的等差数列,  ,
,  ,设数列
,设数列  满足
满足  ,
,  .
.
-
(1) 求数列
 的通项;
的通项;
-
(2) 求数列
 的前
的前  项和
项和  .
.
已知  ,则
,则  =.
=.
 ,则
,则  =.
=.
某几何体的三视图如图所示,则这个几何体外接球的表面积为( )

A . 20π
B . 40π
C . 50π
D . 60π
已知函数 ,
,  ,
,  .
.
 ,
,  ,
,  .
.
-
(1) 当
 ,
,  时,求证:
时,求证: ;
;
-
(2) 若
 恒成立,求
恒成立,求 的最大值.
的最大值.
如图,在△ABC中,∠C=Rt∠,以顶点C为圆心,BC为半径作圆.若  求AB的长度为;⊙C截AB所得弦BD的长为.
求AB的长度为;⊙C截AB所得弦BD的长为.
 求AB的长度为;⊙C截AB所得弦BD的长为.
求AB的长度为;⊙C截AB所得弦BD的长为. 
已知直线  .当
.当  在实数范围内变化时,
在实数范围内变化时,  与
与  的交点
的交点  恒在一个定圆上,则定圆方程是 .
恒在一个定圆上,则定圆方程是 .
 .当
.当  在实数范围内变化时,
在实数范围内变化时,  与
与  的交点
的交点  恒在一个定圆上,则定圆方程是 .
恒在一个定圆上,则定圆方程是 .
某大学志愿者协会有6名男同学,4名女同学,在这10名同学中,3名同学来自数学学院,其余7名同学来自物理、化学等其他互不相同的七个学院,现从这10名同学中随机选取3名同学,到希望小学进行支教活动(每位同学被选到的可能性相同).
-
(1) 求选出的3名同学是来自互不相同学院的概率;
-
(2) 设X为选出的3名同学中女同学的人数,求随机变量X的分布列和数学期望.
如图,将线段  用一条连续不间断的曲线
用一条连续不间断的曲线  连接在一起,需满足要求:曲线
连接在一起,需满足要求:曲线  经过点B , C , 并且在点B , C处的切线分别为直线
经过点B , C , 并且在点B , C处的切线分别为直线  ,那么下列说法正确的是( )
,那么下列说法正确的是( )
 用一条连续不间断的曲线
用一条连续不间断的曲线  连接在一起,需满足要求:曲线
连接在一起,需满足要求:曲线  经过点B , C , 并且在点B , C处的切线分别为直线
经过点B , C , 并且在点B , C处的切线分别为直线  ,那么下列说法正确的是( )
,那么下列说法正确的是( ) 
A . 存在曲线  满足要求
B . 存在曲线
满足要求
B . 存在曲线  满足要求
C . 若曲线
满足要求
C . 若曲线  和
和  满足要求,则对任意满足要求的曲线
满足要求,则对任意满足要求的曲线  ,存在实数
,存在实数  ,使得
,使得  D . 若曲线
D . 若曲线  和
和  满足要求,则对任意实数
满足要求,则对任意实数  ,当
,当  时,曲线
时,曲线  满足要求
满足要求
 满足要求
B . 存在曲线
满足要求
B . 存在曲线  满足要求
C . 若曲线
满足要求
C . 若曲线  和
和  满足要求,则对任意满足要求的曲线
满足要求,则对任意满足要求的曲线  ,存在实数
,存在实数  ,使得
,使得  D . 若曲线
D . 若曲线  和
和  满足要求,则对任意实数
满足要求,则对任意实数  ,当
,当  时,曲线
时,曲线  满足要求
满足要求
设函数 ,
,  ,
,  的图像上的两点
的图像上的两点 ,
,  处的切线分别为
处的切线分别为 ,
,  , 且
, 且 ,
,  ,
,  在y轴上的截距分别为
在y轴上的截距分别为 ,
,  , 若
, 若 , 则
, 则 的取值范围是( )
的取值范围是( )
 ,
,  ,
,  的图像上的两点
的图像上的两点 ,
,  处的切线分别为
处的切线分别为 ,
,  , 且
, 且 ,
,  ,
,  在y轴上的截距分别为
在y轴上的截距分别为 ,
,  , 若
, 若 , 则
, 则 的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
时下,网校教学越来越受到广大学生的喜爱,它已经成为学生们课外学习的一种趋势,假设某网校的套题每日的销售量![]() (单位:千套)与销售价格
(单位:千套)与销售价格![]() (单位:元/套)满足的关系式
(单位:元/套)满足的关系式![]() ,其中
,其中![]() ,
,![]() 为常数.已知销售价格为4元/套时,每日可售出套题21千套.
为常数.已知销售价格为4元/套时,每日可售出套题21千套.
(1)求![]() 的值;(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格
的值;(2)假设网校的员工工资,办公等所有开销折合为每套题2元(只考虑销售出的套数),试确定销售价格![]() 的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
的值,使网校每日销售套题所获得的利润最大.(保留1位小数)
若集合![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D.![]()
如图所示,在![]() 中,
中,![]() ,
,![]() 在线段
在线段![]() ,设
,设![]() ,
,![]() ,
,![]() ,则
,则![]() 的最小值为__________.
的最小值为__________.
已知集合 ,
, ,则
,则 为( )
为( )
A. B.
B. 
C. D.
D. 
A.
C.
最近更新
- 17.《世界卫生组织烟草控制框架公约》在我国已经生效八年了,但目前仍存在烟草企业不积极履行公约相关内容的行为。北京市消费
- 图5中线段长短表示影响程度大小,下列情况与甲、乙、丙、丁四图相符的是( )。 图5工业区位选择模式图 A.甘蔗
- 甲、乙、丙为我国某地300 m ×300 m范围内新建居民区的三个规划方案。三个方案中①~⑥为居民楼,且序号相同的居民楼
- 一质量为m的木块静止在光滑的水平面上,从t=0时刻开始,将一个大小为F的水平恒力作用在该木块上,在t=t1时刻力F的功率
- 已知某一反应体系有反应物和生成物共三种物质:FeCl3、FeCl2、Fe。完成下列问题。 (1)该反应中的还原产物的化学
- 柳宗元认为,秦末农民起义“咎在人怨,非郡邑之制失也”;西汉七国之乱“有叛国而无叛郡”,“秦制 之得亦明矣”。下列哪种说法
- 下列反应中,不属于取代反应的是 ( )
- 在DNA 测序工作中,需要将某些限制性内切酶的限制位点在 DNA上定位,使其成为 DNA 分子中的物理参照点。这项工作叫
- 下列反应的离子方程式书写正确的是() A.实验室用大理石与醋酸反应制取二氧化碳:CaCO3+2H+Ca2++CO2↑+
- .梭伦改革为希腊民主政治奠定了基础。其措施有 ①实行财产等级制度 ②建立十个
- You’vedone much of the work, and please leave ______ to us.A
- 在一定条件下某叶肉细胞内叶绿体和线粒体有关生理活动的叙述,正确的是 A.光照下叶绿体和线粒体直接为对方利用的物质有O2
- 对于可逆反应mA(g)+nB(s)pC(g)+qD(g)反应过程中,其他条件不变时,产物D的质量分数D%与温度T或压强p
- 根据下列表格对应值: x 3.24 3.25 3.26 ax2+bx+c -0.02 0.01 0.03 判断关于x的方
- 正确的化学实验操作对实验结果、人身安全非常重要.下图中的实验操作正确的是()A.闻气体气味 B.取用块状固体 C.滴加液
- “6世纪起,……学者、教师、工匠和僧侣从大陆渡海二来,随身除了带来新的宗教信仰外,还带来了新的生活方式。而那些游历“天
- —I can’t move the bookcase. Could you give me a hand? —
- 依次填入下列各句横线处的词语,最恰当的一组是 ( ) [1]阿Q这个人物也是有生活 的
- 选出下列字形有误的一项:( ) A.按捺 狡黠 冗长 恣意 B.亲家 赝品 梦靥 笑靥 C.禁锢
- 地球公转轨道示意图。读图回答:地球从甲运行到乙期间,重庆的正午太阳高度 A.逐渐减小 B.逐渐增大 C.先减小后增大



