高中 数学
在  中,
中,  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  ,则下列命题正确的是( )
,则下列命题正确的是( )
 中,
中,  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  ,则下列命题正确的是( )
,则下列命题正确的是( )
A .  的充要条件是
的充要条件是 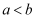 B . 若
B . 若  不是直角三角形,则
不是直角三角形,则  ,
C . 若
,
C . 若  为
为  的最小内角,则
的最小内角,则  D . 不存在
D . 不存在  ,使
,使  成立
成立
 的充要条件是
的充要条件是 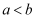 B . 若
B . 若  不是直角三角形,则
不是直角三角形,则  ,
C . 若
,
C . 若  为
为  的最小内角,则
的最小内角,则  D . 不存在
D . 不存在  ,使
,使  成立
成立
设函数  ,若对于
,若对于  ,都有
,都有  成立,则实数
成立,则实数  的取值为.
的取值为.
 ,若对于
,若对于  ,都有
,都有  成立,则实数
成立,则实数  的取值为.
的取值为.
近年来,国资委.党委高度重视扶贫开发工作,坚决贯彻落实中央扶贫工作重大决策部署,在各个贫困县全力推进定点扶贫各项工作,取得了积极成效,某贫困县为了响应国家精准扶贫的号召,特地承包了一块土地,已知土地的使用面积以及相应的管理时间的关系如下表所示:
|
土地使用面积x(单位:亩) |
1 |
2 |
3 |
4 |
5 |
|
管理时间y(单位:月) |
8 |
10 |
13 |
25 |
24 |
并调查了某村  名村民参与管理的意愿,得到的部分数据如下表所示:
名村民参与管理的意愿,得到的部分数据如下表所示:
| 愿意参与管理 | 不愿意参与管理 | |
| 男性村民 | 150 | 50 |
| 女性村民 | 50 |
参考公式:  ,参考数据:
,参考数据:  ,
,  ,
, 
-
(1) 求出相关系数r的大小,并判断管理时间y与土地使用面积x是否线性相关?
-
(2) 若以该村的村民的性别与参与管理意愿的情况估计贫困县的情况,则从该贫困县中任取3人,记取到不愿意参与管理的男性村民的人数为X,求X的分布列及数学期望.
函数  的值域为( )
的值域为( )
 的值域为( )
的值域为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
下列运算正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知正四棱锥 的高为2,
的高为2, , 过该棱锥高的中点且平行于底面
, 过该棱锥高的中点且平行于底面 的平面截该正四棱锥所得截面为A1B1C1D1 , 若底面
的平面截该正四棱锥所得截面为A1B1C1D1 , 若底面 与截面的顶点在同一球面上,则该球的表面积为( )
与截面的顶点在同一球面上,则该球的表面积为( )
 的高为2,
的高为2, , 过该棱锥高的中点且平行于底面
, 过该棱锥高的中点且平行于底面 的平面截该正四棱锥所得截面为A1B1C1D1 , 若底面
的平面截该正四棱锥所得截面为A1B1C1D1 , 若底面 与截面的顶点在同一球面上,则该球的表面积为( )
与截面的顶点在同一球面上,则该球的表面积为( )
A . 20π
B .  C . 4π
D .
C . 4π
D . 
 C . 4π
D .
C . 4π
D . 
已知函数  ,(
,(  且
且  )的图像恒过点
)的图像恒过点  ,若直线
,若直线  经过点M,则a+b的最小值为( )
经过点M,则a+b的最小值为( )
 ,(
,(  且
且  )的图像恒过点
)的图像恒过点  ,若直线
,若直线  经过点M,则a+b的最小值为( )
经过点M,则a+b的最小值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设 是非零向量,则
是非零向量,则 是
是 的( )
的( )
 是非零向量,则
是非零向量,则 是
是 的( )
的( )
A . 充要条件
B . 必要不充分条件
C . 充分不必要条件
D . 既不充分也不必要条件
已知双曲线 的顶点到一条渐近线的距离为实轴长的
的顶点到一条渐近线的距离为实轴长的 , 则双曲线C的离心率为( )
, 则双曲线C的离心率为( )
 的顶点到一条渐近线的距离为实轴长的
的顶点到一条渐近线的距离为实轴长的 , 则双曲线C的离心率为( )
, 则双曲线C的离心率为( )
A .  B . 2
C .
B . 2
C .  D . 3
D . 3
 B . 2
C .
B . 2
C .  D . 3
D . 3
若sinx•cosx<0,则角x的终边位于( )
A . 第一、二象限
B . 第二、三象限
C . 第二、四象限
D . 第三、四象限
如图的几何体中,AB⊥平面ACD,DE⊥平面ACD,△ACD为等边三角形,AD=DE=2AB=2,F为CD的中点.
(1)求证:AF∥平面BCE;
(2)求证:平面BCE⊥平面CDE.

在  n 的展开式中,各项系数和与二项式系数和之比为32,则x2的系数为( )
n 的展开式中,各项系数和与二项式系数和之比为32,则x2的系数为( )
 n 的展开式中,各项系数和与二项式系数和之比为32,则x2的系数为( )
n 的展开式中,各项系数和与二项式系数和之比为32,则x2的系数为( )
A . 50
B . 70
C . 90
D . 120
坐标平面内有两个圆x2+y2=16和x2+y2﹣6x+8y+24=0,这两个圆的内公切线的方程是
 的值为 ( )
的值为 ( )
A . 0
B . 1
C .  D .
D . 
 D .
D . 
已知直线3x+4y﹣24=0与坐标轴的两个交点及坐标原点都在一个圆上,则该圆的半径为( )
A . 3
B . 4
C . 5
D . 6
对于等差数列和等比数列,我国古代很早就有研究成果,北宋大科学家沈括在《梦溪笔谈》中首创的“隙积术”,就是关于高阶等差级数求和的问题.现有一货物堆,从上向下查,第一层有2个货物,第二层比第一层多3个,第三层比第二层多4个,以此类推,记第  层货物的个数为
层货物的个数为  ,则数列
,则数列  的通项公式
的通项公式  ,数列
,数列  的前
的前  项和
项和  .
.
 层货物的个数为
层货物的个数为  ,则数列
,则数列  的通项公式
的通项公式  ,数列
,数列  的前
的前  项和
项和  .
.
函数 的值域为
的值域为 , 则实数
, 则实数 可能的取值有( )
可能的取值有( )
 的值域为
的值域为 , 则实数
, 则实数 可能的取值有( )
可能的取值有( )
A . 5
B . 1
C .  D . 3
D . 3
 D . 3
D . 3
如图,在圆的内接四边形ABCD中,∠ABC=90°,∠ABD=30°,∠BDC=45°,AD=1,则BC=________.
设全集U=R,集合A={x|x≤3},B={x|﹣1<x≤6},则集合(CUA)∩B( )
A.{x|3≤x<6} B.{x|3<x<6} C.{x|3<x≤6} D.{x|3≤x≤6}
已知函数g(x)是R上的奇函数,且当x<0时,g(x)=-ln(1-x),函数f(x)= 若f(2-x2)>f(x),则实数x的取值范围是( )
若f(2-x2)>f(x),则实数x的取值范围是( )
A.(-∞,1)∪(2,+∞) B.(-∞,-2)∪(1,+∞) C.(1,2) D.(-2,1)
最近更新
- 如图1所示,小华将一只正在发声的音叉触及面颊,有振感。由小华的感觉可以验证A.声音产生的原因
- 若,的最大值是3,则的值是 ( ) (A)1 (B)-1 (C)0 (D)2
- 石英砂是制造玻璃的重要原料,其主要成分是二氧化硅(SiO2),其中硅元素的化合价为A.+2 B.+3
- 下列各天气系统中能表示“秋高气爽”天气的是
- 一交流电压随时间变化的规律如图所示,该交流电压的有 效值和周期分别是A. 14.14V,0.0ls B. l0V
- 山西煤炭外运有“神话第一线”的铁路是 A.朔黄线 B.大秦线 C.太焦线
- 22. Victor apologized for________to inform me of the change
- 3、下列词语解释,有误的一项是( ) A、敕造:奉皇帝之命建造。 B、不经之谈:没有经验的话。 C、盘盘:形容山路
- 阅读下面对话,掌握其大意,并根据所给首字母的提示,在标有题号的右边横线上写出一个英语单词完整、正确形式,使对话通顺。 M
- 用“王水”(浓盐酸与浓硝酸的混合物)溶解黄金后得到一种物质:HAuCl4(四氯合金酸),其中金元素的化合价为 A.+1
- 今年“3.15”期间某商场为了吸引顾客,设计了一种促销活动:在一个不透明的箱子里放有4个相同的小球,球上分别标有“0元”
- 在一定温度下,下列叙述不是可逆反应A(气)+3B(气)2C(气)+2D(固)达到平衡的标志的是 ①C的生成速率与C的分解
- 我国古代推动农业生产发展的重要因素不包括( )A、生产工具的改进
- 下列句子标点符号使用正确的一项目( )A、我国古人早已认识到:“人性善恶可变”,关键在教育。B、“哎!”陈红忽然
- 南极洲的象征是( )A.北极熊B.企鹅C.袋鼠D.大象
- 下列叙述中不正确的是( ) A.癌细胞一般能不断合成蛋白质和产生中心粒 B.生物的卵细胞虽然分化程度很高,但仍然具有较
- —— What do you think of the concert?—— Oh, it was______succe
- 由受精卵发育而来的雌蜂(蜂王)是二倍体(2n=32),由未受精的卵细胞发育而来的雄蜂是单倍体(n=16)。下列相关叙述正
- 下图以及《人民日报》报道“小麦亩产12万斤”“水稻亩产3万斤”“一棵白菜500千”的好消息。这些现象发生在( )。
- 阅读下面短文,掌握其大意,然后从方框中选出能填入文中空白处的最合适的单词,并将该单词的标号(A、B、C、D、E…)填写在



