高中 数学
如图,在四棱锥E﹣ABCD中,底面ABCD是边长为2的正方形,且DE=  ,平面ABCD⊥平面ADE,∠ADE=30°
,平面ABCD⊥平面ADE,∠ADE=30°
 ,平面ABCD⊥平面ADE,∠ADE=30°
,平面ABCD⊥平面ADE,∠ADE=30° 
-
(1) 求证:AE⊥平面CDE;
-
(2) 求AB与平面BCE所成角的正弦值.
已知函数 .
.
 .
.
-
(1) 当
 , 且
, 且 时,求
时,求 的值;
的值;
-
(2) 若存在实数
 , 使得函数
, 使得函数 的定义域为
的定义域为 时,其值域为
时,其值域为 , 求实数
, 求实数 的取值范围.
的取值范围.
命题“对任意的x∈R,x3﹣x2+1≤0”的否定是 .
 +
+  =( )
=( )
A . ﹣1﹣i
B . 1+i
C . ﹣1+i
D . 1﹣i
已知  ,求
,求  的值.
的值.
 ,求
,求  的值.
的值.
已知三个函数f(x)=2x+x,g(x)=x-2,h(x)=log2x+x的零点依次为a,b,c,则 ( )
A . a<b<c
B . a<c<b
C . b<a<c
D . c<a<b
已知函数  (
(  且
且  ).
).
 (
(  且
且  ).
).
-
(1) 若函数
 的图象经过点
的图象经过点  ,求
,求  的值;
的值;
-
(2) 比较
 与
与  的大小,并写出比较过程.
的大小,并写出比较过程.
若关于x的不等式2  >(
>(  )2a在实数集上恒成立,则实数a的取值范围.
)2a在实数集上恒成立,则实数a的取值范围.
 >(
>(  )2a在实数集上恒成立,则实数a的取值范围.
)2a在实数集上恒成立,则实数a的取值范围.
已知  是定义域为R的奇函数,当
是定义域为R的奇函数,当  时,
时,  .
.
 是定义域为R的奇函数,当
是定义域为R的奇函数,当  时,
时,  .
.
-
(1) 求
 ;
;
-
(2) 求
 的解析式;
的解析式;
-
(3) 若
 在
在  上的值域为
上的值域为  ,求
,求  的最小值与最大值.
的最小值与最大值.
若数列  满足:
满足:  ,则数列
,则数列  的前n项和
的前n项和  为
为 

 满足:
满足:  ,则数列
,则数列  的前n项和
的前n项和  为
为 

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知集合M={0,x},N={1,2},若M∩N={1},则M∪N=
设向量  =(﹣1,2),
=(﹣1,2),  =(m,1),如果向量
=(m,1),如果向量 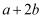 与2
与2 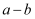 平行,那么
平行,那么  与
与  的数量积等于( )
的数量积等于( )
 =(﹣1,2),
=(﹣1,2),  =(m,1),如果向量
=(m,1),如果向量 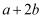 与2
与2 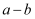 平行,那么
平行,那么  与
与  的数量积等于( )
的数量积等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知随机变量 ξ 的分布列为P(ξ=k)=  ( k=1,2,),则 P(2<x≤4)为( )
( k=1,2,),则 P(2<x≤4)为( )
 ( k=1,2,),则 P(2<x≤4)为( )
( k=1,2,),则 P(2<x≤4)为( )
A .  B .
B .  C .
C . 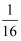 D .
D . 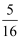
 B .
B .  C .
C . 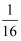 D .
D . 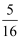
过点(2,1)且与直线x+3y+4=0垂直的直线方程为.
如图,在正方体  中,E,F分别是棱BC,C1D1的中点,则EF与平面BDD1B1的位置关系是.
中,E,F分别是棱BC,C1D1的中点,则EF与平面BDD1B1的位置关系是.
 中,E,F分别是棱BC,C1D1的中点,则EF与平面BDD1B1的位置关系是.
中,E,F分别是棱BC,C1D1的中点,则EF与平面BDD1B1的位置关系是.
已知  ,
,  ,
,  .
.
 ,
,  ,
,  .
.
-
(1) 求
 与
与  的夹角
的夹角  ;
;
-
(2) 求
 .
.
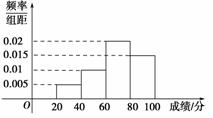
某班![]() 的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
的全体学生参加英语测试,成绩的频率分布直方图如图,数据的分组依次为:[20,40),[40,60),[60,80),[80,100].若低于60分的人数是15,则该班的学生人数是( )
(A)45 (B)50
(C)55 (D)60
将函数![]() 的图象向右平移
的图象向右平移![]() 个单位长度,再向下平移1个单位长度,得到的图象对应的函数解析式为
个单位长度,再向下平移1个单位长度,得到的图象对应的函数解析式为![]()
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
某一棱锥的三视图如右图,则其侧面积为( )
(A).![]() (B).
(B).![]()
(C).![]() (D).
(D).![]()

“二孩政策”的出台,给很多单位安排带来新的挑战,某单位为了更好安排下半年的工作,该单位领导想对本单位女职工做一个调研,已知该单位有女职工300人,其中年龄在40岁以上的有50人,年龄在[30,40]之间的有150人,30岁以下的有100人,现按照分层抽样取30人,则各年龄段抽取的人数分别为( )
A.5,15,10 B.5,10,15 C.10,10,10 D.5,5,20
最近更新
- 下列有关金属腐蚀与防护的说法不正确的是() A.纯银器表面在空气中因化学腐蚀渐渐变暗 B.当镀锡铁制品的镀层破损时,镀层
- 以下哪些机构的设置能体现雅典人民主权与轮番而治的思想 ①公民大会 ②五百人议事会 ③民众法庭 ④保民官的设置 A①②④
- 2011年6月,第三届全国道德模范评选活动进入公示和投票评选阶段,317位候选人用他们的感人事迹,唱响了当代中国社会的道
- 6-0;
- 下列观察测量和实验操作中,正确的是 ( )
- 不等式组的解集是___________.
- E-mail,as well as telephones, an important part in dai
- 某班准备举行“中国古代历史人物图片”展,要求配上历史人物的主要事迹,下列历史人物标号与事迹对应正确的是( )A.①完
- 某DNA分子中A+T占整个DNA分子碱基总数的44%,其中一条链(a)上的G占该链碱基总数的21%,那么,对应的另一条互
- 以“新世纪,新挑战;合作、参与、促进共同繁荣”为主题的APEC上海会议即将召开,中国以积极姿态参
- 常温下,下列各组离子在指定溶液中一定能大量共存的是 A.能使石蕊显红色的溶液:K+、Mg2+、HCO3-、SO42- B
- 下图是我国东南沿海某城市的工业布局规划图。你认为规划合理的是( )
- 两个黄色圆粒豌豆品种进行杂交,得到6000粒种子均为黄色,但有1500粒为皱粒。两个杂交亲本的基因组合可能为 A.Y
- 按照物质的树状分类和交叉分类,HNO3应属于 ①酸 ②氢化物 ③氧化物 ④含氧酸 ⑤难挥发性酸 ⑥强氧化性酸
- 油脂皂化后的混合物分离,可以采用的方法是 A.萃取
- 数列{an}的前n项和记为Sn,已知a1=1,an+1=Sn(n∈N+).证明: (1)数列是等比数列; (2)Sn+1
- 利用显微镜观察人的血细胞涂片,在两种不同的放大倍率下,视野分别为甲和乙,如图所示,下列相关叙述正确的是()A.若玻片往左
- 马克思、恩格斯在《宣言》中指出: “联合的行动,至少是各文明国家的联合的行动,是无产阶级获得解放的首要条件之一。”发展了
- 某相对分子质量为84的烃,主链上有4个碳原子的同分异构体有( )A.3种 B.
- 下列各组词语中,没有错别字的一组是 A、直译 执意不肯 毒素 独竖一帜 B、致力 自立更生



