高中 数学
①最小正周期为π;
②将f(x)的图象向左平移  个单位,所得到的函数是偶函数;
个单位,所得到的函数是偶函数;
③f(0)=1;
④  ;
;
⑤  .
.
其中正确的是( )

 ,若函数
,若函数  是定义在
是定义在  上的奇函数,且对任意
上的奇函数,且对任意  都有
都有  ,当
,当  时,
时,  ,则
,则  .
.
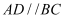 ,
,  ,平面
,平面  平面
平面  ,
,  ,
,  ,
, 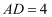 ,
,  ,
,  的余弦值为
的余弦值为  ,
,  ,F为BE中点,G为PD中点.
,F为BE中点,G为PD中点. 
-
(1) 求证:
 平面ABCD;
平面ABCD;
-
(2) 求平面BCE与平面ADE所成角(锐角)的余弦值.
-
(1) 若函数f(x)>0在(0,+∞)上恒成立,求m的取值范围;
-
(2) 若函数f(x)在(0,1)内有零点,求m的取值范围.
 ,集合
,集合  是函数
是函数  的定义域,则下列结论正确的是( )
的定义域,则下列结论正确的是( )
 B . A
B . A B
C . B
B
C . B A
D .
A
D . 
 ,
,  分别是双曲线
分别是双曲线  :
: 
 的左、右焦点.若双曲线
的左、右焦点.若双曲线  与圆
与圆  :
:  的一个交点为
的一个交点为 
 ,且双曲线
,且双曲线  的渐近线为
的渐近线为  ,则
,则  .
.
 ,
,  在
在  上是增函数,则( )
上是增函数,则( )
 为
为  ,
,  在
在  上是减函数
C . p为假命题
D .
上是减函数
C . p为假命题
D .  为
为  ,
,  在
在  上不是增函数
上不是增函数
 中,底面
中,底面 为平行四边形,
为平行四边形, ,
,  丄平面
丄平面 , 且
, 且 ,
,  , 点
, 点 是
是 的中点.
的中点.
-
(1) 求证:
 平面
平面 ;
;
-
(2) 求直线
 与平面
与平面 所成角的正弦值.
所成角的正弦值.
 中,底面
中,底面  是直角梯形,侧棱
是直角梯形,侧棱  底面
底面  ,
,  垂直于
垂直于  和
和  ,
,  为棱
为棱  上的点,
上的点,  ,
,  .
. 
-
(1) 若
 为棱
为棱  的中点,求证:
的中点,求证:  平面
平面  ;
;
-
(2) 当
 时,求平面
时,求平面  与平面
与平面  所成的锐二面角的余弦值;
所成的锐二面角的余弦值;
-
(3) 在第(2)问条件下,设点
 是线段
是线段  上的动点,
上的动点,  与平面
与平面  所成的角为
所成的角为  ,求当
,求当  取最大值时点
取最大值时点  的位置.
的位置.
对![]() ,记
,记![]() 函数
函数![]() ,则方程
,则方程![]() 有三个根,实数a的取值范围是_______.
有三个根,实数a的取值范围是_______.
现有四所大学进行自主招生,同时向一所高中的已获市级竞赛一等奖的甲、乙、丙、丁四位学生发出录取通知书.若这四名学生都愿意进这四所大学的任意一所就读, 则仅有两名学生被录取到同一所大学的概率为____________.
在等高条形图中,下列哪两个比值相差越大,要推断的论述成立的可能性就越大( )

已知扇形AOB的周长为8.
(1)若这个扇形的面积为3,求圆心角的大小;
(2)求这个扇形的面积取得最大值时圆心角的大小和弦长AB.
某营养师要为某个儿童预定午餐和晚餐.已知一个单位的午餐含12个单位的碳水化合物,6个单位的蛋白质和6个单位的维生素![]() ;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素
;一个单位的晚餐含8个单位的碳水化合物,6个单位的蛋白质和10个单位的维生素![]() .另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素
.另外,该儿童这两餐需要的营养中至少含64个单位的碳水化合物,42个单位的蛋白质和54个单位的维生素![]() . 如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
. 如果一个单位的午餐、晚餐的费用分别是2.5元和4元,那么要满足上述的营养要求,并且花费最少,应当为该儿童分别预订多少个单位的午餐和晚餐?
已知等比数列![]() 的前
的前![]() 项和为
项和为![]() 则下列一定成立的是( )
则下列一定成立的是( )
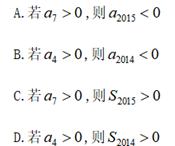
已知椭圆![]() +
+![]() =1(a>b>0)的左顶点为A,左焦点为F,点P为该椭圆上任意一点;若该椭圆的上顶点到焦点的距离为2,离心率e=
=1(a>b>0)的左顶点为A,左焦点为F,点P为该椭圆上任意一点;若该椭圆的上顶点到焦点的距离为2,离心率e=![]() ,则
,则![]() ·
·![]() 的取值范围是( )
的取值范围是( )
A. [-2,2] B. [0,12] C. [5,12] D. [-2,0]
已知向量![]()
![]() =(2k,3),
=(2k,3),![]()
![]() =( 5,1),且
=( 5,1),且![]()
![]() ∥
∥![]()
![]() ,则实数k=( )
,则实数k=( )
A.![]()
![]() B.
B.![]()
![]() C.
C.![]()
![]() D.﹣5
D.﹣5
已知当x<1时,f(x)=(2﹣a)x+1;当x≥1时,f(x)=ax(a>0且a≠1).若对任意x1≠x2 , 都有![]() 成立,则a的取值范围( )
成立,则a的取值范围( )
A、(1,2) B、![]() C、
C、![]() D、(0,1)∪(2,+∞)
D、(0,1)∪(2,+∞)
已知x,y均为正数,且x>y,求证:![]() .
.
- 半径为R的半圆柱形玻璃,横截面如图19-3-4所示,O为圆心,已知玻璃的折射率为,当光由玻璃射向空气时,发生全反射的临界
- 虽然没人很清楚的看到过怪物,但有关的信息从上世纪末就有了。
- 北京奥运会开幕式上,“太古遗音”、四大发明、汉字、戏曲和太极拳表演让人耳目一新,中国灿烂的文化神奇地展示在世人面前。这体
- (6分)请根据反应 Fe + CuSO4 = Fe SO4 + Cu,设计原电池,完成以下问题。 负极:
- 孟元老在《东京梦华录》中写道:“相国寺每月五次开放万姓交易,大三门上皆是飞禽猫犬之类,珍禽奇兽,无所不有。第二、三门皆动
- 某生物的三对等位基因(Aa、Bb、Ee)分别位于三对同源染色体上,且基因A、b、e分别控制①②③三种酶的合成,在三种酶的
- 下列各句中,括号中成语使用恰当的一项是() A.国庆节那天,市政府组织了盛大的烟火晚会,一时间,空中(天花乱坠),
- 已知在水溶液中,乙醇(C2H5OH)不发生电离,溴化氢(HBr)电离产生氢离子(H+) 和溴离子(Br-),氢氧化钠电离
- (本题满分12分)已知集合 (1)求 (2)若求a的取值范围.
- 汉字是世界上最古老的文字之一。下列图片所呈现的汉字字体中,最早出现的是 A
- 下列函数图象与x轴均有公共点,其中能用二分法求零点的是( ) A B
- 电源的作用是提供 。 是使电路中的自由电荷定向移动形成电流的原因。我国家庭用电
- “金银铜铁锡”俗称五金。在这五种金属中,金属活动性最强的是 A.铁 B.金 C.银 D.铜
- 下面有关单倍体的叙述,不正确的是( ) A.由未受精的卵细胞发育而成的个体 B.花药离体培养而形成的个体 C.凡事
- 如图4所示,将带正电的甲球放在不带电的乙球左侧,两球在空间形成了稳定的静电场,实线为电场线,虚线为等势线。A、B两点与两
- 解方程:x2+4x﹣1=0.
- 发展中国特色社会主义文化,要大力加强社会主义核心价值体系建设。社会主义核心价值体系的基础是 A.树立和践行社会主义荣辱观
- 阅读下面这首诗歌,然后回答下面试题。 书边事 张乔① 调角②断清秋,征人倚戍楼。 春风对青冢③,白日落梁州④。 大漠无兵
- (本小题共13分) 某校组织“上海世博会”知识竞赛.已知学生答对第一题的概率是0.6,答对第二题的概率是0.5,并且他们
- As we know, it iscommon for people to catch a cold in winter



