高中 数学
已知数列 满足
满足 ,
,  .
.
 满足
满足 ,
,  .
.
-
(1) 证明
 是等差数列;
是等差数列;
-
(2) 若
 , 求数列
, 求数列 的前
的前 项和.
项和.
在正四面体A-BCD中, , 点O为
, 点O为 的重心,过点O的截面平行于AB和CD,分别交BC,BD,AD,AC于E,F,G,H,则 ( )
的重心,过点O的截面平行于AB和CD,分别交BC,BD,AD,AC于E,F,G,H,则 ( )
 , 点O为
, 点O为 的重心,过点O的截面平行于AB和CD,分别交BC,BD,AD,AC于E,F,G,H,则 ( )
的重心,过点O的截面平行于AB和CD,分别交BC,BD,AD,AC于E,F,G,H,则 ( ) 
A . 四边形EFGH的周长为8
B . 四边形EFGH的面积为2
C . 直线AB和平面EFGH的距离为 D . 直线AC与平面EFGH所成的角为
D . 直线AC与平面EFGH所成的角为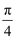
 D . 直线AC与平面EFGH所成的角为
D . 直线AC与平面EFGH所成的角为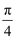
已知圆C1和C2关于直线y=﹣x对称,若圆C1的方程是(x+5)2+y2=4,则圆C2的方程是( )
A . (x+5)2+y2=2
B . x2+(y+5)2=4
C . (x﹣5)2+y2=2
D . x2+(y﹣5)2=4
已知曲线 与曲线
与曲线 , 则下列说法正确的是( )
, 则下列说法正确的是( )
 与曲线
与曲线 , 则下列说法正确的是( )
, 则下列说法正确的是( )
A . 曲线 的焦点到其渐近线的距离是3
B . 当
的焦点到其渐近线的距离是3
B . 当 时,两曲线的焦距相等
C . 当
时,两曲线的焦距相等
C . 当 时,曲线
时,曲线 为椭圆
D . 当
为椭圆
D . 当 时,曲线
时,曲线 为双曲线
为双曲线
 的焦点到其渐近线的距离是3
B . 当
的焦点到其渐近线的距离是3
B . 当 时,两曲线的焦距相等
C . 当
时,两曲线的焦距相等
C . 当 时,曲线
时,曲线 为椭圆
D . 当
为椭圆
D . 当 时,曲线
时,曲线 为双曲线
为双曲线
已知定义在  的函数
的函数  ,对满足
,对满足  的任意实数
的任意实数  ,
,  ,都有
,都有  ,则实数
,则实数  的取值范围为.
的取值范围为.
 的函数
的函数  ,对满足
,对满足  的任意实数
的任意实数  ,
,  ,都有
,都有  ,则实数
,则实数  的取值范围为.
的取值范围为.
已知tanα=2,则cos(2α+π)等于
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
函数  的定义域.
的定义域.
 的定义域.
的定义域.
若函数 则下列说法正确的是( )
则下列说法正确的是( )
 则下列说法正确的是( )
则下列说法正确的是( )
A .  是奇函数
B . 若
是奇函数
B . 若 在定义域上单调递减,则
在定义域上单调递减,则 C . 当
C . 当 时,若
时,若 , 则
, 则 D . 若函数
D . 若函数 有2个零点,则
有2个零点,则
 是奇函数
B . 若
是奇函数
B . 若 在定义域上单调递减,则
在定义域上单调递减,则 C . 当
C . 当 时,若
时,若 , 则
, 则 D . 若函数
D . 若函数 有2个零点,则
有2个零点,则
已知 均为正实数,定义
均为正实数,定义 , 若
, 若 , 则x的值为( )
, 则x的值为( )
 均为正实数,定义
均为正实数,定义 , 若
, 若 , 则x的值为( )
, 则x的值为( )
A . 1
B . 2013
C . 2014
D . -1或2014
若a=  ,b=
,b=  ,则a+b的值为( )
,则a+b的值为( )
 ,b=
,b=  ,则a+b的值为( )
,则a+b的值为( )
A . 1
B . 5
C . ﹣1
D . 2π﹣5
直线 的斜率是( )
的斜率是( )
 的斜率是( )
的斜率是( )
A . 1
B . 2
C . 3
D . 4
在等比数列 中,
中, 分别是下表第一,二,三行中的某一个数,且
分别是下表第一,二,三行中的某一个数,且 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
 中,
中, 分别是下表第一,二,三行中的某一个数,且
分别是下表第一,二,三行中的某一个数,且 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.第一列 | 第二列 | 第三列 | |
第一列 | 3 | 2 | 3 |
第二列 | 4 | 6 | 5 |
第三列 | 9 | 12 | 8 |
-
(1) 写出
 , 并求数列
, 并求数列 的通项公式;
的通项公式;
-
(2) 若数列
 满足
满足 , 求数列
, 求数列 的前n项和
的前n项和 .
.
经过两圆x2+y2=9和(x+4)2+(y+3)2=8交点的直线方程为
设函数f(x)=  ,则使得f(x)>f(2x-1)成立的x的取值范围是( )
,则使得f(x)>f(2x-1)成立的x的取值范围是( )
 ,则使得f(x)>f(2x-1)成立的x的取值范围是( )
,则使得f(x)>f(2x-1)成立的x的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
已知(x+a)2(x﹣1)3的展开式中,x4的系数为1,则a=.
已知  的展开式中各项的系数之和为1024.
的展开式中各项的系数之和为1024.
 的展开式中各项的系数之和为1024.
的展开式中各项的系数之和为1024.
-
(1) 求各奇数项系数之和;
-
(2) 求
 的展开式中不含
的展开式中不含  的各项系数之和.
的各项系数之和.
已知 , 其中
, 其中 ,
,  .
.
 , 其中
, 其中 ,
,  .
.
-
(1) 求
 在
在 上为减函数的充要条件;
上为减函数的充要条件;
-
(2) 求
 在
在 上的最大值;
上的最大值;
-
(3) 解关于x的不等式:
 .
.
设向量a=(1,-1),b=(m+1,2m-4),若a![]() b,则m=______.
b,则m=______.
![]() 若“
若“![]() ”是真命题,则实数
”是真命题,则实数![]() 的最小值为( )
的最小值为( )
A、![]() B、
B、 ![]() C、1 D、
C、1 D、![]()
如图所示的几何体中,四边形![]() 为平行四边形,
为平行四边形,![]() ,
,
![]() ⊥平面
⊥平面![]() ,
,![]() ∥
∥![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,且
,且![]() 是
是![]()
的中点.
(1)求证:![]() ∥平面
∥平面![]() ;
;
(2)求二面角![]() 的大小;
的大小;
(3)在线段![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得 ![]() 与
与![]() 所成的角为
所成的角为![]() ?若存在,求出
?若存在,求出![]() 的长度;若不存在,请说明理由.
的长度;若不存在,请说明理由.

最近更新
- 如图所示,内壁光滑的圆锥筒的轴线垂直于水平面,圆锥筒固定不动,两个质量相同的小球A和B紧贴着内壁分别在如图所示的水平面
- 已知点A(-1,y1),B(1,y2),C(2,y3)都在反比例函数y= (k>0)的图象上,则________<___
- 计算:4sin30°-2cos30°+tan60°=
- 网上购物已然成为一种时尚,同时也有许多陷阱。小杨同学在一家门户网站购买了6种10元一张的光盘,几天后只给她寄来4种,且质
- 物质的用途与性质密切相关。下列说法不正确是 A.铜用于制导线,是由于铜有良好的导电性 B.氮气常用作保护气,是由于氮气的
- 对“草→昆虫→食虫鸟→鹰”这条食物链的叙述正确的是() A.有四个营养级、两个次级消费者 B.有三个营养级、一个生产者
- [甲] 既加冠,益慕圣贤之道。又患无硕师名人与游,尝趋百里外,从乡之先达执经叩问。先达德隆望尊,门人弟子填其室,未尝稍降
- In this age of Internet chat, videogames and reality televis
- 下列有关描述中,正确的是 ( ) A.用以治疗癌症的“生物导弹”
- 关于对动能的理解,下列说法正确的是( ) A.动能是机械能的一种表现形式,凡是运动的物体都具有动能 B.动
- .已知一组数据1,2,2,0,-1,-2,0,-1,则这组数据的平均数为__________,众数为__________
- 下列离子组一定能大量共存的是() A.甲基橙呈黄色的溶液中:I-、Cl-、NO、Na+ B.石蕊呈蓝色的溶液中:Na+、
- 废旧碱性锌锰干电池内部的黑色物质A主要含有MnO2、NH4CI、ZnCI2,还有少量的FeCI2和炭粉,用A制备高纯Mn
- 近来,市场上经常出现有关食品安全的事件,如三鹿奶粉事件、人造蜂蜜事件、“苏丹红”食品事件等。食品安全事件说明市场经济具有
- 关于一名普通中学生人体数据的估测中,下列最接近真实情况的是( ) A.步行速度约为15 m/s B.身高约为168
- 下列各句中,标点符号使用符合规范的一项是( ) A.烟草科技本质上是为了包装香烟,扩大销售,会危及人体健康,它正是国
- 已知=3,求.
- 结合材料,综合探究。(6分) 【材料一】2011年7月,为拯救12岁男孩东东的生命,湖北孝感学院学生田强毅然选择“弃考捐
- 为了减小实验误差,以下操作中必要的是( ) A.在“研究平抛物体运动”的实验中,斜槽应尽可能光滑B.在“验证力
- 在名著阅读分享会上,同学们模拟了儒勒·凡尔纳和刘慈欣的一场穿越时空的对话,请你将下面的对话补充完整。 刘慈欣:尊敬的凡尔



