高中 数学
已知函数 ,
,  .
.
 ,
,  .
.
-
(1) 讨论函数
 的单调性;
的单调性;
-
(2) 若
 时,
时, 恒成立,求实数a的取值范围.
恒成立,求实数a的取值范围.
已知作用于某一质点的力F(x)= (单位:N),试求力F(x)从x=0处运动到x=2处(单位:m)所做的功
(单位:N),试求力F(x)从x=0处运动到x=2处(单位:m)所做的功
 (单位:N),试求力F(x)从x=0处运动到x=2处(单位:m)所做的功
(单位:N),试求力F(x)从x=0处运动到x=2处(单位:m)所做的功
已知函数f(x)=ax-ax(a>0且a≠1).
-
(1) 当a=e时,求函数f(x)的最值;
-
(2) 设g(x)是f(x)的导函数,讨论函数g(x)在区间(0,1)零点的个数.
在  中,
中, 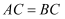 ,
,  为边
为边  的中点,
的中点,  .
.
 中,
中, 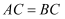 ,
,  为边
为边  的中点,
的中点,  .
.
-
(1) 求
 ;
;
-
(2) 若
 的外接圆半径为
的外接圆半径为  ,求
,求  的外接圆半径.
的外接圆半径.
在矩形  中,
中,  ,
,  ,且
,且  ,沿
,沿  将
将  折起,当四面体
折起,当四面体  的体积最大时,四面体
的体积最大时,四面体  的外接球的表面积的最小值是( )
的外接球的表面积的最小值是( )
 中,
中,  ,
,  ,且
,且  ,沿
,沿  将
将  折起,当四面体
折起,当四面体  的体积最大时,四面体
的体积最大时,四面体  的外接球的表面积的最小值是( )
的外接球的表面积的最小值是( )
A . 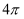 B .
B .  C .
C .  D .
D . 
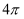 B .
B .  C .
C .  D .
D . 
过抛物线  的焦点
的焦点  的直线交抛物线于
的直线交抛物线于  两点,点
两点,点  是原点,若
是原点,若  ,则
,则  的面积为( )
的面积为( )
 的焦点
的焦点  的直线交抛物线于
的直线交抛物线于  两点,点
两点,点  是原点,若
是原点,若  ,则
,则  的面积为( )
的面积为( )
A .  B .
B .  C .
C .  D .
D .  或
或 
 B .
B .  C .
C .  D .
D .  或
或 
如图,在边长为2的正三角形△ABC中,D为BC的中点,E,F分别在边CA,AB上.

-
(1) 若
 ,求CE的长;
,求CE的长;
-
(2) 若∠EDF=60°,问:当∠CDE取何值时,△DEF的面积最小?并求出面积的最小值.
截角四面体是一种半正八面体,可由四面体经过适当的截角,即截去四面体的四个顶点所产生的多面体.如图所示,将棱长为3的正四面体沿棱的三等分点做平行于底面的截面得到的所有棱长均为1的截角四面体,则下列说法正确的有( )

A . 该截角四面体的表面积为  B . 该截角四面体的体积为
B . 该截角四面体的体积为  C . 该截角四面体中,GH∥JK
D . 二面角 B-AC-D的余弦值为
C . 该截角四面体中,GH∥JK
D . 二面角 B-AC-D的余弦值为 
 B . 该截角四面体的体积为
B . 该截角四面体的体积为  C . 该截角四面体中,GH∥JK
D . 二面角 B-AC-D的余弦值为
C . 该截角四面体中,GH∥JK
D . 二面角 B-AC-D的余弦值为 
已知复数 ,
,  是关于x的方程
是关于x的方程 的两个根,则
的两个根,则 ( )
( )
 ,
,  是关于x的方程
是关于x的方程 的两个根,则
的两个根,则 ( )
( )
A . 9
B . 81
C .  D . 82
D . 82
 D . 82
D . 82
已知向量  ,
,  ,若
,若  ,则
,则 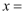 ( )
( )
 ,
,  ,若
,若  ,则
,则 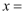 ( )
( )
A .  B .
B . 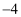 C .
C .  D .
D . 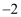
 B .
B . 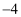 C .
C .  D .
D . 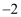
某校为了解高三男生的体能达标情况,抽调了120名男生进行立定跳远测试,根据统计数据得到如下的频率分布直方图.若立定跳远成绩落在区间  的左侧,则认为该学生属“体能不达标的学生,其中
的左侧,则认为该学生属“体能不达标的学生,其中  分别为样本平均数和样本标准差,计算可得
分别为样本平均数和样本标准差,计算可得  (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表).
 的左侧,则认为该学生属“体能不达标的学生,其中
的左侧,则认为该学生属“体能不达标的学生,其中  分别为样本平均数和样本标准差,计算可得
分别为样本平均数和样本标准差,计算可得  (同一组中的数据用该组区间的中点值作代表).
(同一组中的数据用该组区间的中点值作代表). 
-
(1) 若该校高三某男生的跳远距离为
 ,试判断该男生是否属于“体能不达标”的学生?
,试判断该男生是否属于“体能不达标”的学生?
-
(2) 该校利用分层抽样的方法从样本区间
 中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在
中共抽出5人,再从中选出两人进行某体能训练,求选出的两人中恰有一人跳远距离在  的概率.
的概率.
设函数  .
.
 .
.
-
(1) 求
 的单调区间;
的单调区间;
-
(2) 若对任意的
 都有
都有  恒成立,求实数
恒成立,求实数  的取值范围.
的取值范围.
16艘轮船的研究中,船的吨位区间为[192,3 246](单位:吨),船员的人数5~32人,船员人数y关于吨位x的回归方程为  =9.5+0.006 2x,
=9.5+0.006 2x,
 =9.5+0.006 2x,
=9.5+0.006 2x,
-
(1) 若两艘船的吨位相差1 000,求船员平均相差的人数.
-
(2) 估计吨位最大的船和最小的船的船员人数.
已知复数 , 且
, 且 ,
,  , 则
, 则 ( )
( )
 , 且
, 且 ,
,  , 则
, 则 ( )
( )
A . 1
B . -1
C . 0
D . -2
在![]() 中,
中,![]() 分别为角
分别为角![]() 所对的边,
所对的边,![]() 。
。
(1)求边![]() 的值;
的值;
(2)求![]() 的值。
的值。
经济学中,函数![]() 的边际函数
的边际函数![]() 定义为
定义为![]() ,利润函数
,利润函数![]()
的边际利润函数定义为![]() 。某公司最多生产100台报警系统装置,
。某公司最多生产100台报警系统装置,
生产![]() 台的收入函数为
台的收入函数为![]() (单位:元),其成本函数为
(单位:元),其成本函数为![]() (单位:元),利润是收入与成本之差。
(单位:元),利润是收入与成本之差。
(1)求利润函数![]() 的边际利润函数
的边际利润函数![]() ;
;
(2)利润函数![]() 与边际利润函数
与边际利润函数![]() 是否具有相等的最大值;
是否具有相等的最大值;
(3)你认为本题中边际利润函数![]() 取最大值的实际意义是什么?
取最大值的实际意义是什么?
已知定义在R上的函数![]() 为偶函数.且
为偶函数.且![]()
(1)求![]() 的值;
的值;
(2)判断![]() 在
在![]() 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(3)若方程![]() 在
在![]() 上有解,求
上有解,求![]() 的取值范围?
的取值范围?
已知数列![]() 中,
中,![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足
![]() (
(![]() ,
,![]() ).
).
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
数列![]() 满足a
满足a![]() ,na
,na![]() ,
,![]() .
.
(1)证明:数列![]() 是等差数列;
是等差数列;
![]() 2)设
2)设![]()
已知函数![]() .
.
(1)求![]() 时,求
时,求![]() 的单调区间;
的单调区间;
(2)讨论![]() 在定义域上的零点个数.
在定义域上的零点个数.
最近更新
- 某混合溶液中所含离子的浓度如下表,则Mn+离子及a值可能为所含离子 NO3- SO42- H+ Na+ Mn+ 浓度(m
- 在F、P、S三种元素中,每种元素都有某些方面区别于其他两种元素;若从中选出氟元素,选择的理由是 ( ) A.单质与
- 苏俄的新经济政策和罗斯福新政的相似之处是: A.采取多种形式的国有化政策 B.尽量保留“自由企业制度” C
- 读“中国略图”,完成下列问题:(10分)(1)填出图中序号所代表的地理事物名称:山脉:① ②
- 下列分子或离子中,含有孤对电子的是 ( )A.H2O B.CH4 C.
- 图1为“我国南方某区域等高线地形图”。读图,回答6 ~8题。6. 图中所示各河流中,绘制错误的是 A.a B. b
- 利用空气浮力升空的飞行器是: [ ] A.飞艇 B.直升机 C.滑翔机 D.火箭
- 《傅雷家书》被称为“ 苦心孤诣教子篇 ” ,傅雷教育儿子 ________ (姓名)胜不骄、败不馁,要有国家和民族的荣誉
- 下列各离子组可在同一溶液中大量共存,且形成无色溶液的是() A.Fe2+、H+、NO3-、Cl- B.H+、
- 通过一块偏振片去观察电灯、蜡烛、月亮、反光的黑板,当以入射光线为轴转动偏振片时,看到的现象有何不同?
- 有所对胃有较大刺激作用的药物,常装在淀粉制成的胶囊中,原因主要是( ) A、不少药物是蛋白质类物质,避免在胃中
- 已知P是以F1、F2为焦点的双曲线上的一点,若,,则此双曲线的离心率为 A. B.3
- 下列有关人体剧烈运动时内环境稳态调节的叙述,正确的是 A.剧烈运动时所需的葡萄糖,可通过增加胰岛素分泌进行调节 B.肌细
- 函数的单调增区间为( ) A. B. C. D.
- 分别比较下列句中加点字的意义,判断正确的一项是 ①夙遭闵凶②而刘夙婴疾病③门衰祚薄④日薄西山动词,迫近 A、①与
- 与彩电相比,旅游商品属于:( ) A、物质商品; B、耐用消费品; C、服务商品; D、专用商品
- When we donate(捐献)blood, a small amount is usually taken in
- 15.下列有关细胞器的说法正确的是()A.核糖体是噬菌体、细菌、酵母菌唯一共有的细胞器 B.线粒体是有氧呼吸的主要场所,
- 下列各元素的氧化物中, 既能与盐酸反应, 又能够与 NaOH溶液反应的是: ( )A.元素X: 它的原子中M 层比
- 2010年1月12日,海地发生7.0级地震,首都太子港及全国大部分地区受灾情况严重。第二天50名中国国际救援队队员从北京



