高中 数学
若函数f(x)=  ,则f(-3)的值为( )
,则f(-3)的值为( )
 ,则f(-3)的值为( )
,则f(-3)的值为( )
A . 5
B . -1
C . -7
D . 2
某学校社会实践小组共有5名成员,该小组计划前往该地区三个红色教育基地进行“学党史,颂党恩,跟党走”的主题宣讲志愿服务.若每名成员只去一个基地,每个基地至少有一名成员前往,且甲,乙两名成员前往同一基地,则不同的分配方案共有( )
A . 18种
B . 36种
C . 72种
D . 144种
已知  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在四边形  中,
中,  ,点
,点  分别是边
分别是边  的中点,延长
的中点,延长 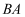 和
和  交
交  的延长线于不同的两点
的延长线于不同的两点  ,则
,则  的值为.
的值为.
 中,
中,  ,点
,点  分别是边
分别是边  的中点,延长
的中点,延长 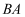 和
和  交
交  的延长线于不同的两点
的延长线于不同的两点  ,则
,则  的值为.
的值为. 
函数  的图象是由函数
的图象是由函数  的图象( )
的图象( )
 的图象是由函数
的图象是由函数  的图象( )
的图象( )
A . 向右平移  个单位而得到
B . 向左平移
个单位而得到
B . 向左平移  个单位而得到
C . 向右平移
个单位而得到
C . 向右平移  个单位而得到
D . 向左平移
个单位而得到
D . 向左平移  个单位而得到
个单位而得到
 个单位而得到
B . 向左平移
个单位而得到
B . 向左平移  个单位而得到
C . 向右平移
个单位而得到
C . 向右平移  个单位而得到
D . 向左平移
个单位而得到
D . 向左平移  个单位而得到
个单位而得到
若过点 最多可作出
最多可作出 条直线与函数
条直线与函数 的图象相切,则( )
的图象相切,则( )
 最多可作出
最多可作出 条直线与函数
条直线与函数 的图象相切,则( )
的图象相切,则( )
A .  B . 当
B . 当 时,
时, 的值不唯一
C .
的值不唯一
C .  可能等于-4
D . 当
可能等于-4
D . 当 时,
时, 的取值范围是
的取值范围是
 B . 当
B . 当 时,
时, 的值不唯一
C .
的值不唯一
C .  可能等于-4
D . 当
可能等于-4
D . 当 时,
时, 的取值范围是
的取值范围是
已知命题  对于
对于  恒有
恒有  成立;命题
成立;命题  奇函数
奇函数  的图象必过原点,则下列结论正确的是( )
的图象必过原点,则下列结论正确的是( )
 对于
对于  恒有
恒有  成立;命题
成立;命题  奇函数
奇函数  的图象必过原点,则下列结论正确的是( )
的图象必过原点,则下列结论正确的是( )
A .  为真
B .
为真
B .  为假
C .
为假
C .  为真
D .
为真
D .  为真
为真
 为真
B .
为真
B .  为假
C .
为假
C .  为真
D .
为真
D .  为真
为真
某制造商为拓展业务,引进了一种生产体育器材的新型设备.通过市场分析发现,每月需投入固定成本3000元,生产x台需另投入成本C(x)元,且  若每台售价1000元,且每月生产的体育器材月内能全部售完.
若每台售价1000元,且每月生产的体育器材月内能全部售完.
 若每台售价1000元,且每月生产的体育器材月内能全部售完.
若每台售价1000元,且每月生产的体育器材月内能全部售完.
-
(1) 求制造商所获月利润L(x)(元)关于月产量x(台)的函数关系式;
-
(2) 当月产量为多少台时,制造商由该设备所获的月利润最大?并求出最大月利润.
从1~7这七个数字中选3个数字,组成无重复数字的三位数,其中偶数的个数为( )
A . 210
B . 120
C . 90
D . 45
集合  的真子集共有( )个
的真子集共有( )个
 的真子集共有( )个
的真子集共有( )个
A . 5
B . 6
C . 7
D . 8
已知数列  的前
的前  项和为
项和为  ,点
,点  在曲线
在曲线  ,上数列
,上数列  满足
满足
 的前
的前  项和为
项和为  ,点
,点  在曲线
在曲线  ,上数列
,上数列  满足
满足 ,
,  ,
,  的前5项和为45.
的前5项和为45.
-
(1) 求
 ,
,  的通项公式;
的通项公式;
-
(2) 设
 ,数列
,数列  的前
的前  项和为
项和为  ,求使不等式
,求使不等式  恒成立的最大正整数
恒成立的最大正整数  的值.
的值.
已知  为锐角,且
为锐角,且  ,则
,则  .
.
 为锐角,且
为锐角,且  ,则
,则  .
.
如图所示为函数f(x)=2sin(ωx+φ)(ω>0,0≤φ≤π)的部分图象,其中A,B两点之间的距离为5,那么f(﹣1)=

设  ,且当
,且当  时
时  有意义,求实数
有意义,求实数  的取值范围.
的取值范围.
 ,且当
,且当  时
时  有意义,求实数
有意义,求实数  的取值范围.
的取值范围.
设正项等比数列 的前
的前 项和为
项和为 , 若
, 若 , 则
, 则 ( )
( )
 的前
的前 项和为
项和为 , 若
, 若 , 则
, 则 ( )
( )
A . 4
B . 3
C . 2
D . 1
已知![]() ,
,![]() 的取值如下表:
的取值如下表:
| x | -3 | -1 | 2 | 6 | 7 | 8 |
| y | 8.0 | 6.5 | 5.0 | -0.5 | -2.0 | -3.0 |
若![]() 之间是线性相关,且线性回归直线方程为
之间是线性相关,且线性回归直线方程为![]() ,则实数
,则实数![]() 的值是( )
的值是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
已知![]() 求下列各式的值:
求下列各式的值:
2,4,6
(1)
![]()
(2)![]()
如图是某学生![]() 次考试成绩的茎叶图,则该学生
次考试成绩的茎叶图,则该学生![]() 次考试成绩的标准差
次考试成绩的标准差![]() = .
= .


已知直线![]() 与直线
与直线![]() 的交点为
的交点为![]() ,椭圆
,椭圆![]() 的焦点为
的焦点为![]() ,则
,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
已知直线![]() 过点
过点![]() 且与直线
且与直线![]() 垂直,则
垂直,则![]() 的方程是( )
的方程是( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
最近更新
- 赤霉素和生长素的部分作用机理如图,下列说法正确的是() A. 由图可知赤霉素的生理作用具有两重性
- 设NA为阿伏加德罗常数的值。下列有关叙述正确的是() A. 1mol苯中共平面的原子数最多为6NA B. 1.3g乙炔和
- 在有机物分子中,若某个碳原子连接着四个不同的原子或原子团,这种碳原子称为 “手性碳原子”。凡有一个手性碳原子的物质一定具
- 计算:﹣(2﹣)﹣(π﹣3.14)0+(1﹣cos30°)×()﹣2;
- 物体在液体中受到的浮力大小 A、和物体本身的重力大小有关 B、和物体的体积大小有关
- -Why couldn’t you get home that day? -Because______12:00
- 请根据提供的上联,对出下联(任选二题)。(4分)①《虞美人》叹尽亡国恨,
- 1962年,英国青年化学家以巴特莱特将PtF6和Xe按等物质的量在室温下混合后,首次得到含有化学键的稀有气体化合物六氟合
- 图5中,a表示垂直于纸面的一根导体,并且是闭合电路的一部分在磁场中沿如图中箭头所示的方向运动时,不会产生感应电流的是
- 如图3所示,竖直放置螺线管与导线abcd构成回路,导线所围区域内有垂直纸面向里的变化的匀强磁场,螺线管下方桌面上有一导体
- 1862年,马克思在《中国纪事》一文中说:“他们给予民众的惊慌比给予老统治者的惊慌还要厉害。”“除了改朝换代以外,他们没
- 阅读下面的文字,完成下列各题。 头发(有删节) 这个夏天热得有些早了。在我还没怎么喘过气来时,公司就宣布破产了。受这次国
- .如图是一种可充电的锂离子电池充放电的工作示意图。放电时该电池的电极反应式为: 负极:LixC6-xe-=C6+xLi+
- A.2∶1∶2 B.1∶2∶2 C.1∶1∶1 D.2∶2∶3
- 下列说法正确的是 A.声波和电磁波都是由物体的振动产生的 B.声波和电磁波,频率越大,波长越大 C.声波的传播速度与介质
- 关于匀变速直线运动中的加速度的方向和正负值问题,下列说法中错误的是…( )A.在匀加速直线运动中,加速度方向一定和
- 在很多加油站都有这样的提示:“请熄火加油”、“请不要使用手机”等。这样是为了防止火花点燃汽油引起火灾,因为常温下汽油容易
- He is very popular among his students as he always tries to
- 飞速发展的高铁给中国人的生活带来了巨大的便利,但温州动车追尾事故却让40个人的生命足迹永远定格。这起事故给高铁敲响了警钟
- 某校在开展 “校园献爱心”活动中,准备向南部山区学校捐赠男、女两种款式的书包.已知男款书包的单价50元/个,女款书包的单



