高中 数学
若关于
 方程
方程
 (
(
 是实数)有两个不等复数根
是实数)有两个不等复数根
 ,其中
,其中
 (
(
 是虚数单位),下面四个选项正确的有( )
是虚数单位),下面四个选项正确的有( )
 方程
方程
 (
(
 是实数)有两个不等复数根
是实数)有两个不等复数根
 ,其中
,其中
 (
(
 是虚数单位),下面四个选项正确的有( )
是虚数单位),下面四个选项正确的有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在平面直角坐标系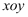 中,已知椭圆
中,已知椭圆 的右准线为
的右准线为 (定义:椭圆C的右准线方程为
(定义:椭圆C的右准线方程为 , 其中
, 其中 ).点P是右准线上的动点,过点P作椭圆C的两条切线,分别与y轴交于M,N两点.当P在x轴上时,
).点P是右准线上的动点,过点P作椭圆C的两条切线,分别与y轴交于M,N两点.当P在x轴上时, .
.
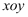 中,已知椭圆
中,已知椭圆 的右准线为
的右准线为 (定义:椭圆C的右准线方程为
(定义:椭圆C的右准线方程为 , 其中
, 其中 ).点P是右准线上的动点,过点P作椭圆C的两条切线,分别与y轴交于M,N两点.当P在x轴上时,
).点P是右准线上的动点,过点P作椭圆C的两条切线,分别与y轴交于M,N两点.当P在x轴上时, .
.
-
(1) 求椭圆C的方程;
-
(2) 求
 的最小值.
的最小值.
集合{0,2,3}的真子集共有( )
A . 5个
B . 6个
C . 7个
D . 8个
已知命题p:向量  =(1,2)与向量
=(1,2)与向量  =(2,k)的夹角为锐角的充要条件是k>﹣1;命题q:函数f(x)=
=(2,k)的夹角为锐角的充要条件是k>﹣1;命题q:函数f(x)=  是偶函数,下列是真命题的是( )
是偶函数,下列是真命题的是( )
 =(1,2)与向量
=(1,2)与向量  =(2,k)的夹角为锐角的充要条件是k>﹣1;命题q:函数f(x)=
=(2,k)的夹角为锐角的充要条件是k>﹣1;命题q:函数f(x)=  是偶函数,下列是真命题的是( )
是偶函数,下列是真命题的是( )
A . p∧q
B . (¬p)∧q
C . p∧(¬q)
D . p∨(¬q)
某校高一(9)班共有49名同学,在学校举办的书法竞赛中有24名同学参加,在数学竞赛中有25名参加,已知这两项都参赛的有12名同学,在这两项比赛中,该班没有参加过比赛的同学的人数为( )
A . 10
B . 11
C . 12
D . 13
已知三次函数 在
在 是增函数,则m的取值范围是( )
是增函数,则m的取值范围是( )
 在
在 是增函数,则m的取值范围是( )
是增函数,则m的取值范围是( )
A . m<2或m>4
B . -4<m<-2
C . 2<m<4
D . 以上皆不正确
已知函数  图象相邻两对称轴间的距离为4,则a的值是( )
图象相邻两对称轴间的距离为4,则a的值是( )
 图象相邻两对称轴间的距离为4,则a的值是( )
图象相邻两对称轴间的距离为4,则a的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某小区有1000户,各户每月的用电量近似服从正态分布N(300,100),则用电量在320度以上的户数估计约为( )
[参考数据:若随机变量ξ服从正态分布N(μ,σ2),则P(μ﹣σ<ξ<μ+σ)=68.26%,P(μ﹣2σ<ξ<μ+2σ)=95.44%,P(μ﹣3σ<ξ<μ+3σ)=99.74%].
A . 17
B . 23
C . 34
D . 46
已知,如图,在梯形ABCD中,AD∥BC,AD=3,BC=7,点M,N分别是对角线BD,AC的中点,则MN=( )

A . 2
B . 5
C .  D .
D . 
 D .
D . 
已知向量  =(3,﹣4),
=(3,﹣4),  =(6,﹣3),
=(6,﹣3),  =(5﹣m,﹣(3+m)),若A、B、C三点共线,则实数m的值为.
=(5﹣m,﹣(3+m)),若A、B、C三点共线,则实数m的值为.
 =(3,﹣4),
=(3,﹣4),  =(6,﹣3),
=(6,﹣3),  =(5﹣m,﹣(3+m)),若A、B、C三点共线,则实数m的值为.
=(5﹣m,﹣(3+m)),若A、B、C三点共线,则实数m的值为.
如图所示的程序框图,若输出值  ,则输入值
,则输入值  的集合是( )
的集合是( )
 ,则输入值
,则输入值  的集合是( )
的集合是( ) 
A .  B .
B .  C .
C .  D . {1}
D . {1}
 B .
B .  C .
C .  D . {1}
D . {1}
某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1﹣50号,并分组,第一组1﹣5号,第二组6﹣10号,…,第十组46﹣50号,若在第三组中抽得号码为12,则在第八组中抽得号码为( )
A . 37
B . 38
C . 39
D . 40
若集合 ,则
,则 ( )
( )
 ,则
,则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知定义在  上的奇函数
上的奇函数  ,当
,当 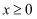 时,
时,  ,则
,则  ( )
( )
 上的奇函数
上的奇函数  ,当
,当 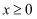 时,
时,  ,则
,则  ( )
( )
A .  B .
B . 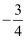 C . 3
D . -3
C . 3
D . -3
 B .
B . 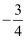 C . 3
D . -3
C . 3
D . -3
在复平面内,若  所对应的点位于第二象限,则实数
所对应的点位于第二象限,则实数  的取值范围是( )
的取值范围是( )
 所对应的点位于第二象限,则实数
所对应的点位于第二象限,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某单位为绿化环境,移栽了甲、乙两种大树各2株.设甲、乙两种大树移栽的成活率分别为  和
和  ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
 和
和  ,且各株大树是否成活互不影响.求移栽的4株大树中:
,且各株大树是否成活互不影响.求移栽的4株大树中:
-
(1) 两种大树各成活1株的概率;
-
(2) 成活的株数ξ的分布列与期望.
若抛物线 上一点
上一点 到其焦点的距离为
到其焦点的距离为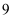 , 则点
, 则点 的坐标为( )
的坐标为( )
 上一点
上一点 到其焦点的距离为
到其焦点的距离为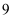 , 则点
, 则点 的坐标为( )
的坐标为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,设函数
,设函数  若关于
若关于  的不等式
的不等式  在
在  上恒成立,则
上恒成立,则  的取值范围为( )
的取值范围为( )
 ,设函数
,设函数  若关于
若关于  的不等式
的不等式  在
在  上恒成立,则
上恒成立,则  的取值范围为( )
的取值范围为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设 , 若直线
, 若直线 与
与 轴相交于点
轴相交于点 , 与
, 与 轴相交于点B,且坐标原点O到直线
轴相交于点B,且坐标原点O到直线 的距离为
的距离为 , 则
, 则 的面积
的面积 的最小值为( )
的最小值为( )
 , 若直线
, 若直线 与
与 轴相交于点
轴相交于点 , 与
, 与 轴相交于点B,且坐标原点O到直线
轴相交于点B,且坐标原点O到直线 的距离为
的距离为 , 则
, 则 的面积
的面积 的最小值为( )
的最小值为( )
A .  B . 2
C . 3
D . 4
B . 2
C . 3
D . 4
 B . 2
C . 3
D . 4
B . 2
C . 3
D . 4
命题“若一个数是负数,则它的平方是正数”的逆命题是 ( )
A.“若一个数是负数,则它的平方不是正数”
B.“若一个数的平方不是正数,则它不是负数”
C.“若一个数不是负数,则它的平方不是正数”
D.“若一个数的平方是正数,则它是负数”
最近更新
- 禹死后,__________继承父位,从而__________制代替了禅让制。
- 19.依次填入下面一段文字横线处的语句,衔接最恰当的一句是( ) “社会情绪能力”是继“情商”之后,目前国际上脑研究
- 下列加点字的注音完全正确的一项是() A.濒临bīn 拖曳yè 媲美pì 稼穑qiáng B.吊唁yà
- 设0≤x≤2,y=4x--3·2x+5,试求该函数的最值.
- 阅读下面短文,回答文后题目。《闻一多先生的说和做》(16分)闻一多先生还有另外一个方面,——作为革命家的方面。这个方面,
- 阅读材料,解决问题:材料1:在研究数的整除时发现:能被5、25、125、625整除的数的特征是:分别看这个数的末一位、末
- 编写一个程序,输入正方形的边长,输出它的对角线长和面积的值。
- 在一密闭容器中,有甲、乙、丙、丁四种物质,一定条件下充分反应,测得反应前后各物质的质量如下表:物质甲乙 丙丁 反应前的质
- 下列描述正确的是 A.用吸管吸饮料时,用力吸的作用是增大管内的气压 B.悬挂在天花板上的灯静止时,受到的重力与绳子对灯的
- Early in the morning, I was taken in a nylon bag into a truc
- 为了解高二年级学生暑假期间的学习情况,抽取甲、乙两班,调查这两个班的学生暑假期间每天平均学习的时间(单位:小时),统计结
- 一列简谐横波在t=0时刻的波形图如图所示,t=0.35s时Q质点第二次到达正向最大位移处,而此时P质点正通过平衡位置向-
- 一定质量的气体,下列叙述中正确的是( )A.如果体积减小,气体分子在单位时间内对单位面积器壁的碰撞次数一定增大B.
- He looked around and caught a man ________his hand into the
- 根据如图回答问题: (1)写出图中有标号的仪器名称:① ② (2)实验室用加热高
- Time should be made good use _______our lessons well.A. of l
- 利用胡萝卜根的组织或细胞繁殖后代的方法属于 。
- (本题满分14分) 已知公差大于零的等差数列的前n项和为Sn,且满足: ,. (1)求数列的通项公式; (2)若数列是等
- 下图是“城市化进程示意图”,读图完成关于不同时期城市化发展特点的叙述,正确的是A.起始阶段,城市化水平低,以矿业城市为主
- 读图6“中国攀枝花工业区(甲)和德国鲁尔区(乙)图”,据此完成19~20题。图6 19.两工业区发展钢铁工业相同的



