高中 数学
若角  是第四象限角,则
是第四象限角,则  是哪个象限角( )
是哪个象限角( )
 是第四象限角,则
是第四象限角,则  是哪个象限角( )
是哪个象限角( )
A . 第一象限角或第二象限角
B . 第二象限角或第三象限角
C . 第一象限角或第三象限角
D . 第二象限角或第四象限角
已知sin =-
=- ,
,  , 则cos
, 则cos 的值为( )
的值为( )
 =-
=- ,
,  , 则cos
, 则cos 的值为( )
的值为( )
A .  B . -
B . - C .
C . 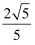 D . -
D . -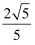
 B . -
B . - C .
C . 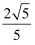 D . -
D . -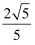
已知全集U={1,2,3,5,6,7,8},集合A={1,3,5},B={5,6,7,8),则A∩(∁UB)=( )
A .  B .
B .  C .
C .  D .
D .  3,
3, 
 B .
B .  C .
C .  D .
D .  3,
3, 
已知椭圆  的离心率
的离心率  ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
 的离心率
的离心率  ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
-
(1) 求椭圆的方程;
-
(2) 设直线l与椭圆相交于不同的两点A,B,已知点A的坐标为(﹣a,0),点Q(0,y0)在线段AB的垂直平分线上,且
 ,求y0的值.
,求y0的值.
写出满足下列条件的一个抛物线方程  .
.
 .
. ⑴该抛物线方程是标准方程;
⑵过  的任意一条直线与该抛物线C有交点,且对于C上的任意一点P,
的任意一条直线与该抛物线C有交点,且对于C上的任意一点P,  的最小值为2.
的最小值为2.
某学校为了解学生的体质健康状况,对高一、高二两个年级的学生进行了体质测试.现从两个年级学生中各随机选取20人,将他们的测试数据,用茎叶图表示如图:《国家学生体质健康标准》的等级标准如表.规定:测试数据≥60,体质健康为合格.
|
等级 |
优秀 |
良好 |
及格 |
不及格 |
|
测试数据 |
| | | |
(Ⅰ)从该校高二年级学生中随机选取一名学生,试估计这名学生体质健康合格的概率;
(Ⅱ)从两个年级等级为优秀的样本中各随机选取一名学生,求选取的两名学生的测试数据平均数大于95的概率;
(Ⅲ)设该校高一学生测试数据的平均数和方差分别为  ,高二学生测试数据的平均数和方差分别为
,高二学生测试数据的平均数和方差分别为  ,试估计
,试估计  、
、  的大小.(只需写出结论)
的大小.(只需写出结论)

如图,P为椭圆  上的一动点,过点P作椭圆
上的一动点,过点P作椭圆  的两条切线PA,PB,斜率分别为
的两条切线PA,PB,斜率分别为  ,
,  .若
.若  为定值,则
为定值,则  ( )
( )
 上的一动点,过点P作椭圆
上的一动点,过点P作椭圆  的两条切线PA,PB,斜率分别为
的两条切线PA,PB,斜率分别为  ,
,  .若
.若  为定值,则
为定值,则  ( )
( ) 
A .  B .
B . 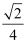 C .
C .  D .
D . 
 B .
B . 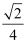 C .
C .  D .
D . 
身穿红、黄两种颜色衣服的各有2人,现将这4人排成一行,要求穿相同颜色衣服的人不能相邻,则不同的排法共有( )
A . 4种
B . 6种
C . 8种
D . 12种
现有4名医生分别到A,B,C三所医院支援抗疫,每名医生有且只能去一所医院且每所医院至少去一名医生,则甲、乙两医生恰好到同一医院支援的概率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知抛物线C的顶点在坐标原点,对称轴是x轴,它的弦PQ所在直线的方程为y=2x﹣1,弦长等于 , 求抛物线的C方程.
, 求抛物线的C方程.
 , 求抛物线的C方程.
, 求抛物线的C方程.
在  内,使
内,使  成立的
成立的  的取值范围是( )
的取值范围是( )
 内,使
内,使  成立的
成立的  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,四边形ABCD中, .
.
 .
. 
-
(1) 若
 , 求△ABC的面积;
, 求△ABC的面积;
-
(2) 若
 ,
,  ,
,  , 求∠ACB的值.
, 求∠ACB的值.
下列四个周期函数中,与其它三个函数周期不一致的函数是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  ,若函数
,若函数  的图象与
的图象与  的图象有3个交点,则
的图象有3个交点,则  的取值范围是( )
的取值范围是( )
 ,若函数
,若函数  的图象与
的图象与  的图象有3个交点,则
的图象有3个交点,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设变量x,y满足约束条件  则目标函数z=3x+y的最大值为( )
则目标函数z=3x+y的最大值为( )
 则目标函数z=3x+y的最大值为( )
则目标函数z=3x+y的最大值为( )
A . 7
B . 8
C . 9
D . 14
下列函数中,既是奇函数又是增函数的是( )
A .  B .
B . 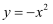 C .
C . 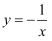 D .
D . 
 B .
B . 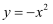 C .
C . 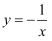 D .
D . 
若集合A={x|x﹣x2>0},B={x|(x+1)(m﹣x)>0},则“m>1”是“A∩B≠∅”的( )
A . 充分而不必要条件
B . 必要而不充分条件
C . 充要条件
D . 既不充分也不必要条件
已知椭圆![]() (常数
(常数![]() ),点
),点![]() 是
是![]() 上的动点,
上的动点,![]() 是右顶点,定点
是右顶点,定点![]() 的坐标为
的坐标为![]() 。
。
(1)若![]() 与
与![]() 重合,求
重合,求![]() 的焦点坐标;
的焦点坐标;
(2)若![]() ,求
,求![]() 的最大值与最小值;
的最大值与最小值;
(3)若![]() 的最小值为
的最小值为![]() ,求
,求![]() 的取值范围。
的取值范围。
已知![]() 满足
满足 ,则
,则![]() 的取值范围为____________.
的取值范围为____________.
过双曲线 :
: 的右顶点作
的右顶点作 轴的垂线,与
轴的垂线,与 的一条渐近线相交于点
的一条渐近线相交于点 .若以
.若以 的右焦点为圆心、半径为4的圆经过
的右焦点为圆心、半径为4的圆经过 ,
, 两点(
两点( 为坐标原点),则双曲线
为坐标原点),则双曲线 的方程为( )
的方程为( )
A. B.
B. 
C. D.
D. 
A.
C.
最近更新
- 一个已充电的电容器,若使它的电量减少3×10-4C,则其电压减少为原来的1/3,则 ( ) A.电容器原来的带电
- 若|a|=5,|b|=3,ab<0,则a+b=_____.
- Being extremely_____to thecold,I do not like skating.
- In1974, after filling out fifty applications, going through
- 隋朝政权的基础是( ) A、北齐 B、东魏 C、西魏
- 2015年3月,第十二届全国人民代表大会第三次会议以2761票赞成、81票反对、33票弃权,表决通过了《全国人民代表大会
- 进口石油依存度是指一个国家或地区进口石油量占石油消费总量的比重,地区石油依存度是指一个国家或地区在某个国家或地区进口的石
- A little boy invited his mother to theteacher-parent meeting
- The manager of the company told us that very little ____ was
- 将0.2 mol AgNO3、0.4 mol Cu(NO3)2、0.6 mol KCl溶于水,配成100 mL溶液,用惰
- 白蚁分泌的蚁酸的化学性质与盐酸相似,能腐蚀很多建筑材料。下列材料中最不容易被白蚁蛀蚀的是A.钢
- 书面表达 假如你是某杂志社编辑Mr. Knowledgeable,根据中学生 Bob的来信内容,给他写封回信,帮助解决他
- (二)(20分)微博为什么这样“红”萧尧如今网络上,微博大行其道。那么微博大热的原因是什么?它对我们而言意味着什么?就内
- In theforest, there is an elephant and a monkey. They’re f
- 根据元素周期表和元素周期律,判断下列有关描述正确的是( )。 A.原子序数为11与9的元素能够形成离子化合物,该化合
- 下表为范德华力的分配情况(kJ・mol-1):(1)考察表中HCl、HBr、HI的色散力、取向力、诱导力以及它们构成的范
- 水平传输装置如图所示,在载物台左端给物块一个恒定的初速度,当传输带顺时针方向转动时,通过传输带所用时间为t1;当传输带逆
- 如图7所示,A、B两木块放在水平面上,它们之间用细线相连,两次连接情况中细线倾斜方向不同但倾角一样,两木块与水平面间的摩
- (1)观察如图4所示量筒,每小格代表的体积是_______,量筒的测量范围是_______。 (2)用天平测小石子
- 下列有关城市规划的叙述,错误的是 A.是一个城市最终发展的计划和各项建设的部署,是建设和管理城市的依据 B.合理的城市规







