高中 数学
甲、乙两位“准笑星”在“信阳笑星”选拔赛中,5位评委给出的评分情况如图所示,记甲、乙两人的平均得分分别为  、
、  ,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
 、
、  ,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
,记甲、乙两人得分的标准差分别为s1、s2 , 则下列判断正确的是( )
A .  <
<  ,s1<s2
,s1<s2  B .
B .  <
<  ,s1>s2
,s1>s2 C .
C .  >
>  ,s1<s2
,s1<s2  D .
D .  >
>  ,s1>s2
,s1>s2
 <
<  ,s1<s2
,s1<s2  B .
B .  <
<  ,s1>s2
,s1>s2 C .
C .  >
>  ,s1<s2
,s1<s2  D .
D .  >
>  ,s1>s2
,s1>s2
若a,b是异面直线,P是a,b外的一点,有以下四个命题
①过P点一定存在直线l与a,b都相交;
②过P点一定存在平面与a,b都平行;
③过P点可作直线与a,b都垂直;
④过P点可作直线与a,b所成角都等于50°.
这四个命题中正确命题的序号是( )
A . ①
B . ②
C . ③④
D . ①②③
已知非零向量 ,
,  满足|
满足| |=
|= |
| |,(
|,(
 ﹣
﹣ )⊥
)⊥ , 则向量
, 则向量 与
与 的夹角大小为( )
的夹角大小为( )
 ,
,  满足|
满足| |=
|= |
| |,(
|,(
 ﹣
﹣ )⊥
)⊥ , 则向量
, 则向量 与
与 的夹角大小为( )
的夹角大小为( )
A . 30°
B . 60°
C . 120°
D . 150°
曲线  在点
在点  处的切线方程为.
处的切线方程为.
 在点
在点  处的切线方程为.
处的切线方程为.
下列函数  ;
;  ;
;  ;
;  与函数
与函数 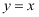 是同一函数的是.
是同一函数的是.
 ;
;  ;
;  ;
;  与函数
与函数 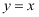 是同一函数的是.
是同一函数的是.
已知函数  ,则以下结论错误的是( )
,则以下结论错误的是( )
 ,则以下结论错误的是( )
,则以下结论错误的是( )
A .  为偶函数
B .
为偶函数
B .  的最小正周期为
的最小正周期为  C .
C .  的最大值为2
D .
的最大值为2
D .  在
在  上单调递增
上单调递增
 为偶函数
B .
为偶函数
B .  的最小正周期为
的最小正周期为  C .
C .  的最大值为2
D .
的最大值为2
D .  在
在  上单调递增
上单调递增
已知U是全集,A,B是U的两个子集,用交、并、补关系将图中的阴影部分表示出来

某党员连续七天在“学习强国”  上获得的学习积分如图所示,则该党员这七天在“学习强国”
上获得的学习积分如图所示,则该党员这七天在“学习强国”  上获得的学习积分的方差为.
上获得的学习积分的方差为.
 上获得的学习积分如图所示,则该党员这七天在“学习强国”
上获得的学习积分如图所示,则该党员这七天在“学习强国”  上获得的学习积分的方差为.
上获得的学习积分的方差为. 
在(x﹣1)(x+1)8的展开式中x5的系数是( )
A . ﹣14
B . 14
C . ﹣28
D . 28
一个由半球和四棱锥组成的几何体,其三视图如图所示. 则该几何体的体积为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知向量 =(2,﹣3),
=(2,﹣3), =(3,λ),且
=(3,λ),且 =
= , 则λ等于( )
, 则λ等于( )
 =(2,﹣3),
=(2,﹣3), =(3,λ),且
=(3,λ),且 =
= , 则λ等于( )
, 则λ等于( )
A .  B . -2
C . -
B . -2
C . - D . -
D . -
 B . -2
C . -
B . -2
C . - D . -
D . -
已知函数 , 若
, 若 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
 , 若
, 若 恒成立,则实数a的取值范围是( )
恒成立,则实数a的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如右图所示,在两个圆盘中,指针在本圆盘每个数所在区域的机会均为  ,那么两个指针至少有一落在奇数所在区域的概率是( )
,那么两个指针至少有一落在奇数所在区域的概率是( )
 ,那么两个指针至少有一落在奇数所在区域的概率是( )
,那么两个指针至少有一落在奇数所在区域的概率是( ) 
A . 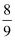 B .
B . 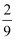 C .
C .  D .
D . 
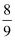 B .
B . 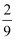 C .
C .  D .
D . 
如图,在底面为梯形的四棱锥  中,已知
中,已知 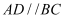 ,
,  ,
,  ,
,  .
.
 中,已知
中,已知 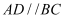 ,
,  ,
,  ,
,  .
. 
-
(1) 求证:
 ;
;
-
(2) 求三棱锥
 的体积.
的体积.
已知![]() 是任意实数,则关于
是任意实数,则关于![]() 的不等式
的不等式![]() 的解集为________.
的解集为________.
已知曲线C1:![]() (
(![]() 为参数),曲线C2:
为参数),曲线C2: (t为参数).
(t为参数).
(Ⅰ)指出C1,C2各是什么曲线,并说明C1与C2公共点的个数;
(Ⅱ)若把C1,C2上各点的纵坐标都压缩为原来的一半,分别得到曲线![]() .写出
.写出![]() 的参数方程.
的参数方程. ![]() 与
与![]() 公共点的个数和C
公共点的个数和C![]() 公共点的个数是否相同?说明你的理由.
公共点的个数是否相同?说明你的理由.
(1)用辗转相除法求840与1 764的最大公约数.
(2)用更相减损术求440与556的最大公约数.
![]() 圆
圆![]() 是以
是以![]() 为直径的圆,延长
为直径的圆,延长![]() 与
与![]() 交于
交于![]() 点.
点.
(Ⅰ)求证:![]() 是圆
是圆![]() 的切线;
的切线;
(Ⅱ)![]() ,求
,求![]() 的长.
的长.
 |
给出两个命题:
命题甲:关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ;
;
命题乙:函数![]() 为增函数。
为增函数。
分别求出符合下列条件的实数a的取值范围:
(1)甲,乙至少有一个是真命题;
(2)甲,乙中有且只有一个是真命题。
求下列函数的值域.
y=3x2-x+2,x∈[1,3]
最近更新
- 已知2,求()的值
- 下图为我国近代工人劳作的场景,对他们的描述错误的是 () A.与资产阶级同时产生
- 阅读下文,完成文后各题。 张益州画像记 苏洵 至和元年秋,蜀人传言,有寇至边。边军夜呼,野无居人;妖言流闻,京师震惊。方
- 下列各物质所含原子数目,按由大到小顺序排列的是 ①0.5mol NH3 ②标准状况下22.4L He ③4℃ 9mL 水
- 遵义会议后,红军攻克娄山关,填写了《忆秦娥·娄山关》一词: “雄关漫道真如铁,而今迈步从头越。”对这一词句的理解,最贴
- 烯烃复分解反应可示意如下: 下列化合物中,经过烯烃复分解反应可以生成的是
- 下列常用词语的字音完全正确的一项是 A.一柱擎天qíng 引吭高歌háng 忧心忡忡chōng B.游目骋
- 已知有下图所示物质相互转换关系试回答: (1)写出B的化学式 ,D的化学式
- (12分)下表是元素周期表的一部分,其中所列字母分别代表某一元素。 a b c d p e f g h i 用表中所给的
- 如图所示,位于水平桌面上的物块P,由跨过定滑轮的轻绳与物块相连,从滑轮到P和到Q的两段绳都是水平的,已知Q与P之间以及桌
- (2013南昌铁一中摸底)航模兴趣小组设计出一架遥控飞行器,其质量m =2kg,动力系统提供的恒定升力F =28 N.试
- 设0<a<b且f(x)=,则下列结论中正确的是()A.f(a)<f()<f(ab)B.f()<f(b)<f(ab)
- 2009年5月11日,民政部公布数据显示,截至4月30日,汶川地震全国共接受国内外捐款659.96亿元,捐赠物资折合人民
- 两种金属粉末的混合物30g与足量的稀硫酸反应,生成1g氢气。则这种混合物的可能组成是( )。A.Mg和Al
- 下列各组词语中,错别字最多的一组是 ( ) A.祛除 座落 账簿 尾大不吊 如雷灌耳
- 下列叙述正确的是( ) A.Fe分别与氯气和稀盐酸反应所得氯化物相同 B.Al、Fe、Cu三者的单质
- 下列说法中正确的是( ) A、每一周期的元素都是从碱金属开始,最后以稀有气体结束 B、同一周期中(除第一
- 苏联解体后,俄罗斯不仅有人全盘否定十月革命,否定列宁,还有人主张把列宁墓从红场迁出,甚至四处寻找沙皇的后裔,企图在俄罗斯
- 物价变动与老百姓的生活息息相关。某中学高三(1)班的同学以“物价上涨与对 策”为主题开展探究活动,他们通过上网查阅获
- 为防止山林火灾,保护森林资源,省政府森林防火总指挥部组织了“征集森林防火宣传用语”活动,清你运用对偶形式拟写一则森林防火



