高中 数学
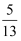 ,且α为第四象限角,则tanα的值等于( )
,且α为第四象限角,则tanα的值等于( )
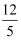 B . ﹣
B . ﹣ 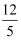 C . ﹣
C . ﹣ 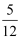 D .
D . 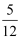
 B .
B . 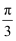 C .
C .  D .
D . 
 ,
,  ]
B . [﹣
]
B . [﹣  π,
π,  ]
C . [
]
C . [  π,2π)
D . [0,
π,2π)
D . [0,  ]∪[
]∪[  π,2π)
π,2π)

 B .
B .  C .
C .  D .
D . 
 与
与 B .
B .  与
与 C .
C .  与
与 D .
D .  与
与
 过点
过点  ,根据下列条件分别求直线l的方程:
,根据下列条件分别求直线l的方程:
-
(1) 直线
 的倾斜角等于
的倾斜角等于  ;
;
-
(2) 直线
 在
在  轴、
轴、  轴上的截距之和等于0.
轴上的截距之和等于0.
 是纯虚数,则实数
是纯虚数,则实数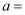 ( )
( )
 满足
满足  ,则
,则  .
.
 ,那么
,那么  的值为.
的值为. 
 (α为参数)化为普通方程,则这个方程是
(α为参数)化为普通方程,则这个方程是
 ,
,  .
. 求:
-
(1)
 ;
;
-
(2)
 .
.
 ,
,  ,则
,则  ( )
( )
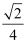 B .
B .  C .
C .  D .
D . 
 中,若
中,若 , 则B的值为( )
, 则B的值为( )  B .
B .  C .
C .  D .
D . 
已知函数f(x)是定义在R上的函数,如果函数f(x)在R上的导函数f′(x)的图象如图,则有以下几个命题:
(1)f(x)的单调递减区间是(-2,0)、(2,+∞),f(x)的单调递增区间是(-∞,-2)、(0,2);
(2)f(x)只在x=-2处取得极大值;
(3)f(x)在x=-2与x=2处取得极大值;
(4)f(x)在x=0处取得极小值.
其中正确命题的个数为 ( )
化简![]()
![]() 的结果是 .
的结果是 .
由世界自然基金会发起的“地球1小时”活动,已发展成为最有影响力的环保活动之一,今年的参与人数再创新高.然而也有部分公众对该活动的实际效果与负面影响提出了疑问.对此,某新闻媒体进行了网上调查,所有参与调查的人中,持“支持”、“保留”和“不支持”态度的人数如下表所示:
| 支持 | 保留 | 不支持 | |
| 20岁以下 | 800 | 450 | 200 |
| 20岁以上(含20岁) | 100 | 150 | 300 |
(Ⅰ)在所有参与调查的人中,用分层抽样的方法抽取![]() 个人,已知从“支持”态度的人中抽取了45人,求
个人,已知从“支持”态度的人中抽取了45人,求![]() 的值;
的值;
(Ⅱ)在持“不支持”态度的人中,用分层抽样的方法抽取5人看成一个总体,从这5人中任意选取2人,求至少有![]() 人20岁以下的概率;
人20岁以下的概率;
(Ⅲ)在接受调查的人中,有8人给这项活动打出的分数如下:9.4,8.6,9.2,9.6,8.7,9.3,9.0,8.2.把这8个人打出的分数看作一个总体,从中任取![]() 个数,求该数与总体平均数之差的绝对值超过0.6的概率.
个数,求该数与总体平均数之差的绝对值超过0.6的概率.
下列命题不正确的是( )
A.根据古典概型概率计算公式P(A)=![]() 求出的值是事件A发生的概率的精确值
求出的值是事件A发生的概率的精确值
B.根据几何概型概率计算公式P(A)=![]() 求出的值是事件A发生的概率的精确值
求出的值是事件A发生的概率的精确值
C.根据古典概型试验,用计算机或计算器产生随机整数统计试验次数N和事件A发生的次数N1,得到的值![]() 是P(A)的近似值
是P(A)的近似值
D.根据几何概型试验,用计算机或计算器产生均匀随机数统计试验次数N和事件A发生次数N1,得到的值![]() 是P(A)的精确值
是P(A)的精确值
设![]() 满足约束条件
满足约束条件 ,若目标函数
,若目标函数![]() 的最大值为35,则
的最大值为35,则![]() 的最小值为 .
的最小值为 .
已知![]() 分别是椭圆
分别是椭圆![]() 的左、右焦点,
的左、右焦点,![]() 是以
是以![]() 为直径的圆与该椭圆的一个交点,且
为直径的圆与该椭圆的一个交点,且![]() ,则这个椭圆的离心率是( )
,则这个椭圆的离心率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
- 阅读下面的文字,完成下面题目。 辛弃疾的生态观 安立志 ①“生态平衡”显然是现代词语,英国的生态学家布赖恩?巴克斯
- 下列哪项是动物的学习行为A.母鸡生蛋 B.老鼠钻洞 C.蜜蜂酿蜜 D.黄牛耕田
- [生物——选修3现代生物科技专题] 下图示牛胚胎移植的基本程序,请据图回答:(1)图中a、b、c过程分别是
- 正在通电的条形电磁铁的铁心突然断成两截,则两截铁心将( ) A、互相吸引. B、互相排斥. C、不发生相互作用
- 于传统工业区的叙述,正确的是() A.传统工业区以传统的中小型企业为主,无大型的现代化企业 B.传统工业因污染问题严重,
- 大气污染与使用能源的种类密切相关。读图,完成第9-10题。 9. 关于四省市农村不同生活能源对大气SO2污染的贡献率
- 英国是历史上最早实行议会君主制政体的典型国家,这种政体不同于美国总统制共和制的特点的最大表现是
- 2006年5月,央视主持人催永元带领21名体验者重走长征路。这支队伍在出发前,计划在我们贵州境内应走的地方有 ①遵义
- 已知为锐角,下列结论 ① ②如果,那么③如果,那么④ 正确的有( ) A. 1个
- 如图甲所示是某同学探究加速度与力的关系的实验装置.他在气垫导轨上安装了一个光电门B,滑块上固定一遮光条,滑块用细线绕过气
- 【山东省泰安市】3.下列句子中加点词语的意思不同的一项是( ) A.①雾凇沆砀,天与云与山与水,上下一白。(《湖
- 若将一瓶浓盐酸和一瓶浓硫酸都敞口放置在空气中,则可以肯定它们( ) A.质量都增大 B.溶质的质量都
- 假如现有的学习水平为“1”,如果每天在这个基础上多努力1%,获得的就是“l+1%”, 一年365天,如果每天坚持这样
- 阅读下面的文字,完成文后题目。 蛮师傅 韩少功 莫求带着两个村干部,来到我家言不及义地东拉西扯,喝茶,抽烟,翻翻桌上的报
- “鱼对水说:你看不到我的眼泪,因为我在水里。水对鱼说:我能感觉到你的眼泪,因为你在我心里。”对这段话的理解中,最恰当的
- 铁镍蓄电池又称爱迪生电池,放电反应 Fe+Ni2O3+3H2O=Fe(OH)2+2Ni(OH)2 则下列说法正确的是 A
- 研究问题:“已知关于x的不等式的解集为(1,2),解关于x的不等式”,有如下解法: 解:由,令,则,1), 所以不等式的
- 《查士丁尼民法大全》中对婚姻的定义是“男女之间的结合,是终身的结合,是人法和 神法的结合”,这就改变了罗马法中原有的“允
- —What’s wrong? —Nothing serious. I’m just ________ busy.A. m
- 苏州园林里都有假山和池沼。假山的堆叠,可以说是一项艺术而不仅是技术。或者是重峦叠嶂,或者是几座小山配合着竹子花木,全在乎



