高中 数学
在直角坐标系  中,曲线
中,曲线  的参数方程为
的参数方程为  (
(  为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以  轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线  的极坐标方程为
的极坐标方程为  .
.
 中,曲线
中,曲线  的参数方程为
的参数方程为  (
(  为参数).以坐标原点为极点,以
为参数).以坐标原点为极点,以  轴的正半轴为极轴,建立极坐标系,曲线
轴的正半轴为极轴,建立极坐标系,曲线  的极坐标方程为
的极坐标方程为  .
.
-
(1) 写出
 的普通方程和
的普通方程和  的直角坐标方程;
的直角坐标方程;
-
(2) 设点
 在
在  上,点
上,点  在
在  上,求
上,求  的最小值及此时
的最小值及此时  的直角坐标.
的直角坐标.
解不等式a2x+7<a3x﹣2(a>0,a≠1).

函数  且
且  的图象过定点P , 则点P的坐标为 .
的图象过定点P , 则点P的坐标为 .
 且
且  的图象过定点P , 则点P的坐标为 .
的图象过定点P , 则点P的坐标为 .
方程组 的解集是( )
的解集是( )
 的解集是( )
的解集是( )
A . (5,4)
B . (5,-4)
C . {(-5,4)}
D . {(5,-4)}
要得到函数  的图象,只需将函数
的图象,只需将函数  的图象( )
的图象( )
 的图象,只需将函数
的图象,只需将函数  的图象( )
的图象( )
A . 向左平移  个单位长度
B . 向右平移
个单位长度
B . 向右平移  个单位长度
C . 向左平移
个单位长度
C . 向左平移  个单位长度
D . 向左平移
个单位长度
D . 向左平移  个单位长度
个单位长度
 个单位长度
B . 向右平移
个单位长度
B . 向右平移  个单位长度
C . 向左平移
个单位长度
C . 向左平移  个单位长度
D . 向左平移
个单位长度
D . 向左平移  个单位长度
个单位长度
已知直线 与曲线
与曲线 相切.则实数
相切.则实数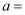 .
.
 与曲线
与曲线 相切.则实数
相切.则实数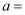 .
.
已知袋中有编号为1、2、3、……、8的八只相同小球,现从中任取3只,则所取3只球的最大编号是5的概率等于( )
A .  B .
B .  C .
C . 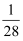 D .
D . 
 B .
B .  C .
C . 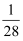 D .
D . 
已知函数f(x)=ax-x-a(a>0,a≠1),那么函数f(x)的零点个数是( )
A . 0个
B . 1个
C . 2个
D . 至少1个
已知函数  .
.
 .
.
-
(1) 若
 是定义在
是定义在  上的偶函数,求实数
上的偶函数,求实数  的值;
的值;
-
(2) 在(1)的条件下,若
 ,求函数
,求函数  的零点.
的零点.
在极坐标系中,圆心为  且过极点的圆的极坐标方程为.
且过极点的圆的极坐标方程为.
 且过极点的圆的极坐标方程为.
且过极点的圆的极坐标方程为.
如图,直三棱柱  中,
中,  ,
,  ,
,  分别为
分别为  、
、  的中点.
的中点.
 中,
中,  ,
,  ,
,  分别为
分别为  、
、  的中点.
的中点. 
-
(1) 证明:
 平面
平面  ;
;
-
(2) 已知
 与平面
与平面  所成的角为
所成的角为  ,求二面角
,求二面角  的余弦值.
的余弦值.
已知点P在圆x2+y2=1上,点A的坐标为(﹣2,0),O为原点,则 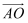 •
•  的最大值为.
的最大值为.
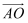 •
•  的最大值为.
的最大值为.
在  中,三个内角
中,三个内角  的对边分别为
的对边分别为  ,若
,若  ,
,  ,
,  ,则
,则  .
.
 中,三个内角
中,三个内角  的对边分别为
的对边分别为  ,若
,若  ,
,  ,
,  ,则
,则  .
.
在①  ,②
,②  ,③
,③  这三个条件中任选一个,补充在下面问题中,并完成解答.问题:已知等差数列
这三个条件中任选一个,补充在下面问题中,并完成解答.问题:已知等差数列  的前
的前  项和为
项和为  ,
,  , ▲ , 若数列
, ▲ , 若数列  满足
满足  ,求数列
,求数列  的前
的前  项和
项和  .
.
 ,②
,②  ,③
,③  这三个条件中任选一个,补充在下面问题中,并完成解答.问题:已知等差数列
这三个条件中任选一个,补充在下面问题中,并完成解答.问题:已知等差数列  的前
的前  项和为
项和为  ,
,  , ▲ , 若数列
, ▲ , 若数列  满足
满足  ,求数列
,求数列  的前
的前  项和
项和  .
.
△ABC的内角A、B、C的对边分别为a、b、c,已知△ABC的面积为accosB,BC的中点为D.
(Ⅰ) 求cosB的值;
(Ⅱ) 若c=2,asinA=5csinC,求AD的长.
已知向量  若
若  ,则
,则  .
.
 若
若  ,则
,则  .
.
对于 上可导的任意函数
上可导的任意函数 , 若满足
, 若满足 , 则必有( )
, 则必有( )
 上可导的任意函数
上可导的任意函数 , 若满足
, 若满足 , 则必有( )
, 则必有( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图:在三棱锥  中,平面
中,平面  平面ABC,
平面ABC, 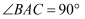 ,
,  ,且
,且  ,
,  .
.
 中,平面
中,平面  平面ABC,
平面ABC, 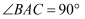 ,
,  ,且
,且  ,
,  .
. 
-
(1) 若点D为BP上的一动点,求证:
 ;
;
-
(2) 若
 ,求二面角
,求二面角  的平面角的余弦值.
的平面角的余弦值.
对于函数![]() 若存在
若存在![]() ,使
,使![]() 成立,则称
成立,则称![]() 为
为![]() 的不动点。已知函数
的不动点。已知函数![]()
(1)当![]() 时,求
时,求![]() 的不动点;
的不动点;
(2)若对于任意实数![]() ,函数
,函数![]() 恒有两个相异不动点,求
恒有两个相异不动点,求![]() 的取值范围
的取值范围![]() 。
。
最近更新
- We can’t go abroad this year, so we will have to_____ oursel
- New evidence shows that getting enough Vitamin D may be the
- 小明设计了一个测量物体质量的“托盘秤”,图(甲)是其原理示意图,其中托盘上放置物体,压力传感器R的电阻值会随所受压力大小
- 下列离子反应不能发生的是() A.KHCO3+HCl===KCl+CO2↑+H2O B.AgNO3+NaCl===AgC
- (2012年2月天水一中检测)如图所示,半径为 r且水平放置的光滑绝缘的环形管道内,有一个电荷量为 e,质量为 m 的电
- 下列图示实验操作中,错误的是 ( )
- 下列地理事物与亚洲面积大,跨纬度广无关的是( ) A.气候复杂多样 B.大河源远流长 C.人文
- 极坐标ρ=cos(-θ)表示的曲线是( )A.双曲线 B.椭圆 C.抛物线
- 阅读下面两首诗,完成下面各题。(10分) 落 花 【唐】李商隐 高阁客竟去,小园花乱飞。 参差连曲陌,迢递送斜晖。 肠断
- 古代诗歌阅读 赋得自君之出矣 张九龄 自君之出矣,不复理残机①。 思君如满月,夜夜减清辉。 ①注:机,织机。 这首诗塑造
- 读“我国部分区域图”,回答10~11题。10.图中阴影所示地区的城市化发展模式是() A.对外开放→外资企业建立→工业化
- “四月的早晨,广阔低平的田野一望无际,船儿在密如蛛网的河流中穿梭。微风徐来,田里绿油油的稻秧迎风起舞,田边的采桑姑娘欢
- 如图,AB∥CD,AE交CD于点C,DE⊥AE,垂足为E,∠A=37°.求∠D的度数. (4分)
- 读美国农业分布图,完成7~8题。 7.图中①附近工农业生产的主要类型是()A.传统工业和乳畜业B.高技术产业和商品谷物农
- 已知是定义在R上的单调减函数,若,则x的范围是( ) A.x>1 B. x<1
- 已知点M在椭圆上,椭圆方程为+=1,M点到左准线的距离为2.5,则它到右焦点的距离为 A.7.5
- 石块A自塔顶自由下落时,石块B从离塔顶处自由下落,后来两石块同时到达地面,由此可知此塔高为( ) A
- 2009年12月,山东省启动了“放飞梦想”绿色手机文化创作传播活动;2010年3月,又开展了“诵读经典,爱我中华”活动。
- Everyyear, a flower show _____ in Beijing Botanical Garden
- 下列有关细胞分化、凋亡和衰老的说法正确的是 ( ) A.细胞分化可以使细胞的种类和数量增加 B.细胞



