高中 数学
 和
和  ,定义运算“*”:
,定义运算“*”:  ,设
,设  ,且关于
,且关于  的方程为
的方程为  恰有三个互不相等的实数根
恰有三个互不相等的实数根  ,则
,则  的取值范围是.
的取值范围是. B .
B .  C .
C .  D .
D . 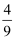
 的长轴长为
的长轴长为  ,离心率为
,离心率为  ,
, 
-
(1) 求椭圆
 的方程;
的方程;
-
(2) 过椭圆
 上的点
上的点 
 的直线
的直线  与
与  ,
,  轴的交点分别为
轴的交点分别为  ,
,  ,且
,且  ,过原点
,过原点  的直线
的直线  与
与  平行,且与
平行,且与  交于
交于  ,
,  两点,求
两点,求 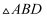 面积的最大值.
面积的最大值.
 上,a为曲线在点P处的切线的倾斜角,则a的取值范围是.
上,a为曲线在点P处的切线的倾斜角,则a的取值范围是.
 则
则  ( )
( )
 , 其中
, 其中 为Peukert常数.在电池容量不变的条件下,当放电电流
为Peukert常数.在电池容量不变的条件下,当放电电流 时,放电时间
时,放电时间 , 则当放电电流
, 则当放电电流 , 放电时间为( )
, 放电时间为( )
 ,
,  ,若点
,若点  在线段
在线段  上,则
上,则  的最大值为.
的最大值为.
 +
+ )n展开式中的倒数第三项的二项式系数为45.
)n展开式中的倒数第三项的二项式系数为45.(1)求n;
(2)求含有x3的项;
(3)求二项式系数最大的项.
 ,
,  ,
,  ,满足
,满足  ,
,  对任意实数
对任意实数  恒成立,
恒成立,  ,则
,则  的最大值为( )
的最大值为( )
 B .
B .  C .
C .  D .
D . 
 的零点个数为( )
的零点个数为( )
 中,
中,  ,
,  .
.
-
(1) 求证:数列
 是等差数列;
是等差数列;
-
(2) 求数列
 的前
的前  项和
项和  .
.

-
(1) 求不等式
 的解集;
的解集;
-
(2) 若不等式
 对任意
对任意  恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.
如图所示的程序框图的算法思路源于我国古代数学名著《九章算术》中的“更相减损术”,执行该程序框图,若输入的![]() 分别为14,18,则输出的
分别为14,18,则输出的![]() ( )
( )

A. 0 B. 2 C. 4 D. 14
《西游记》《三国演义》《水浒传》和《红楼梦》是中国古典文学瑰宝,并称为中国古典小说四大名著.某中学为了解本校学生阅读四大名著的情况,随机调查了100位学生,其中阅读过《西游记》或《红楼梦》的学生共有90位,阅读过《红楼梦》的学生共有80位,阅读过《西游记》且阅读过《红楼梦》的学生共有60位,则该校阅读过《西游记》的学生人数与该校学生总数比值的估计值为
A.0.5 B.0.6 C.0.7 D.0.8
数学家欧拉在1765年提出,任意三角形的外心、重心、垂心位于同一条直线上,后人称这条直线为欧拉线.已知△ABC的顶点A(2,0),B(0,4),若其欧拉线的方程为x-y+2=0,则顶点C的坐标为
A. (-4,0) B. (-3,-1) C. (-5,0) D. (-4,-2)
点![]() 到
到![]() 轴的距离为________.
轴的距离为________.
已知函数f(x)=ax3+bx2+cx,其导函数y=f′(x)的图象经过点(1,0),(2,0),如图所示,则下列说法中不正确的是________.

①当x=![]() 时,函数f(x)取得极小值;②f(x)有两个极值点;③当x=2时,函数f(x)取得极小值;④当x=1时,函数f(x)取得极大值.
时,函数f(x)取得极小值;②f(x)有两个极值点;③当x=2时,函数f(x)取得极小值;④当x=1时,函数f(x)取得极大值.
.一位中学生在30天中坚持每天记忆英语单词,其中有2天的日记忆量是51个,有3天日记忆量是52个,有6天的日记忆量是53个,有8天的日记忆量是54个,有7天的日记忆量是55个,有3天的日记忆量是56个,有1天的日记忆量是57个,计算这位中学生在这30天里的平均日记忆量是多少?
函数![]() 的大致图象为( )
的大致图象为( )

A B C D
- 如图所示,质量不计的弹簧竖直固定在水平面上,t=0时刻,将一金属小球从弹簧正上方某一高度处由静止释放,小球接触弹簧并将弹
- (杭州市2009届高三第一次高考科目质检)“世界上没有免费的午餐”。这句名言出自美国著名经济学家米尔顿—费里德曼之口,他
- 以下电子排布式不是基态原子的电子排布的是() A.1s22s1
- 中华环保世纪行宣传活动主题是“治理水污染、保护水环境”,聚焦工业、城镇污水处理和农村人口饮水安全保障等重点。下列做法违背
- 某天文兴趣小组的学生,在某地观测太阳的视运动情况,发现太阳在空中是从左向右运行的,并将其观测情况绘成下图。读图并完成问题
- 2010年 ,世界博览会在上海市举行。博览会的主题是“城市,让生活更美好”。 A.4月1日至9月31日
- 有A、B、C、D四块金属片,进行如下实验:①A、B用导线相连后,同时浸入稀硫酸中,A 极为负极;②C、D用导线相连后,同
- 假如伦敦奥运会组委会正在向全世界招聘奥运会志愿者。条件如下: 1.有热情为他人服务的思想; 2.有丰富的文化知识,既能做
- 若复数不是纯虚数,则的取值范围是( ) A.或 B.且 C. D.
- 在数轴上画出表示的点。(3分)
- (08深圳市九校联考)一种新发现的细菌中有a、b、c等基因,下图表示用限制性内切酶处理后得到的片段。下列有关叙述中正确的
- 已知抛物线,过定点作两条互相垂直的直线,与抛物线交于两点,与抛物线交于两点,设的斜率为.若某同学已正确求得弦的中垂线在y
- 计算(1)(2x+y-3)(2x-y+3) (2)
- 如图所示,一定质量的同种理想气体从a、b、c、d四个不同的初状态变化到同一末状态e,它们的压强变化情况是 A.从a到e,
- 17.(江西重点中学2012届联考)下列关于生物大分子的叙述错误的是() A.氨基酸的空间结构和种类决定了蛋白质功能 B
- 1......
- 将隶书发展为楷书的是( ) A 、钟瑶 B、王羲之 C、王献之 D、顾恺之
- More often than not, the person sitting next toyou on a plan
- 平面直角坐标系中,O为坐标原点,已知A(3,1),B(-1,3),若点C满足=α+β,其中α、β∈R,且α+β=1,则点
- C Today, air travel is far safer than driving a car on a bus



