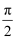高中 数学
已知向量  =(sinωx,cosωx),
=(sinωx,cosωx),  =(cosωx,
=(cosωx,  cosωx)(ω>0),函数f(x)=
cosωx)(ω>0),函数f(x)=  •
•  ﹣
﹣  的图象的一个对称中心与和它相邻的一条对称轴之间的距离为
的图象的一个对称中心与和它相邻的一条对称轴之间的距离为  .
.
 =(sinωx,cosωx),
=(sinωx,cosωx),  =(cosωx,
=(cosωx,  cosωx)(ω>0),函数f(x)=
cosωx)(ω>0),函数f(x)=  •
•  ﹣
﹣  的图象的一个对称中心与和它相邻的一条对称轴之间的距离为
的图象的一个对称中心与和它相邻的一条对称轴之间的距离为  .
.
-
(1) 求函数f(x)的单调递增区间
-
(2) 在△ABC中,角A、B、C所的对边分别是a、b、c,若f(A)=
 且a=1,b=
且a=1,b=  ,求S△ABC .
,求S△ABC .
在复平面内,复数 对应的点位于( )
对应的点位于( )
 对应的点位于( )
对应的点位于( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
若实数x,y满足约束条件  ,则
,则  的最小值为.
的最小值为.
 ,则
,则  的最小值为.
的最小值为.
计算:  .
.
 .
.
已知双曲线  的左、右焦点分别为
的左、右焦点分别为  、
、  ,过
,过  作平行于
作平行于  的渐近线的直线交
的渐近线的直线交  于点
于点  ,若
,若  ,则
,则  的渐近线方程为( )
的渐近线方程为( )
 的左、右焦点分别为
的左、右焦点分别为  、
、  ,过
,过  作平行于
作平行于  的渐近线的直线交
的渐近线的直线交  于点
于点  ,若
,若  ,则
,则  的渐近线方程为( )
的渐近线方程为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在四棱锥P﹣ABCD中,底面梯形ABCD中,AB∥DC,平面PAD⊥平面ABCD,△PAD是等边三角形,已知BD=2AD=4,AB=2DC=2BC=2  ,
,  =m
=m  ,且m>0.
,且m>0.
 ,
,  =m
=m  ,且m>0.
,且m>0. 
-
(1) 求证:平面PAD⊥平面MBD;
-
(2) 求二面角A﹣PB﹣D的余弦值;
-
(3) 试确定m的值,使三棱锥P﹣ABD体积为三棱锥P﹣MBD体积的3倍.
函数  的值域是( )
的值域是( )
 的值域是( )
的值域是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,四边形ABCD是矩形,平面ABCD⊥平面BCE,BE⊥EC.

-
(1) 求证:平面AEC⊥平面ABE;
-
(2) 点F在BE上,若DE∥平面ACF,DC=CE=
 BC=3,求三棱锥A﹣BCF的体积.
BC=3,求三棱锥A﹣BCF的体积.
已知椭圆C: 
 的右焦点为
的右焦点为  ,右顶点为A,以
,右顶点为A,以  为直径的圆交直线
为直径的圆交直线  于点B(不同于原点O),设
于点B(不同于原点O),设  的面积为S.若
的面积为S.若  ,则椭圆C的离心率为( )
,则椭圆C的离心率为( )

 的右焦点为
的右焦点为  ,右顶点为A,以
,右顶点为A,以  为直径的圆交直线
为直径的圆交直线  于点B(不同于原点O),设
于点B(不同于原点O),设  的面积为S.若
的面积为S.若  ,则椭圆C的离心率为( )
,则椭圆C的离心率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
k代表实数,讨论方程kx2+2y2﹣8=0所表示的曲线.
已知实数x、y满足  ,目标函数z=x+ay.
,目标函数z=x+ay.
 ,目标函数z=x+ay.
,目标函数z=x+ay.
-
(1) 当a=﹣2时,求目标函数z的取值范围;
-
(2) 若使目标函数取得最小值的最优解有无数个,求
 的最大值.
的最大值.
已知函数 (
( ,
,  )在一个周期内的部分对应值如下表:
)在一个周期内的部分对应值如下表:
 (
( ,
,  )在一个周期内的部分对应值如下表:
)在一个周期内的部分对应值如下表:
|
| 0 |
|
|
|
| 1 |
|
|
-
(1) 求
 的解析式;
的解析式;
-
(2) 求函数
 的最小值.
的最小值.
已知  分别为双曲线
分别为双曲线  的左、右焦点,以原点为圆心,半焦距为半径的圆交双曲线右支于
的左、右焦点,以原点为圆心,半焦距为半径的圆交双曲线右支于  两点,且
两点,且  为等边三角形,则双曲线的离心率为( )
为等边三角形,则双曲线的离心率为( )
 分别为双曲线
分别为双曲线  的左、右焦点,以原点为圆心,半焦距为半径的圆交双曲线右支于
的左、右焦点,以原点为圆心,半焦距为半径的圆交双曲线右支于  两点,且
两点,且  为等边三角形,则双曲线的离心率为( )
为等边三角形,则双曲线的离心率为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,在平行四边形  中,
中, 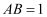 ,
,  ,
, 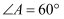 ,沿对角线
,沿对角线  将
将 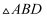 折起到
折起到  的位置,使得平面
的位置,使得平面  平面
平面  ,过
,过  的平面与
的平面与 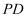 交于
交于  ,则
,则  面积的最小值为( )
面积的最小值为( )
 中,
中, 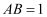 ,
,  ,
, 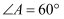 ,沿对角线
,沿对角线  将
将 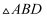 折起到
折起到  的位置,使得平面
的位置,使得平面  平面
平面  ,过
,过  的平面与
的平面与 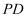 交于
交于  ,则
,则  面积的最小值为( )
面积的最小值为( ) 
A .  B .
B . 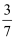 C .
C .  D .
D . 
 B .
B . 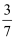 C .
C .  D .
D . 
已知函数 的图象在
的图象在 点处的切线为.
点处的切线为.
 的图象在
的图象在 点处的切线为.
点处的切线为.
-
(1) 求
 ;
;
-
(2) 求证:
 ;
;
-
(3) 已知
 , 若
, 若 对
对 恒成立,求正实数
恒成立,求正实数 的取值范围.
的取值范围.
已知复数z,满足z2=5-12i,求![]() .
.
(本小题12分)已知函数![]()
(1)求![]() 的最大值及此时
的最大值及此时![]() 的值
的值
(2)求![]() 的值.
的值.
命题p:![]() 是命题q:
是命题q:![]() 的( )
的( )
A.必要不充分条件 B.充分不必要条件
C.充要条件 D.既不充分也不必要条件
已知等差数列![]() 中,
中,![]() ,则
,则![]() 的值是 ( )
的值是 ( )
A.15 B.30 C.31 D.64
函数y=Asin(ωx+φ)在一个周期内的图象如图,此函数的解析式为( )
 A.y=2sin(2x+
A.y=2sin(2x+![]() ) B.y=2sin(2x+
) B.y=2sin(2x+![]() )
)
C.y=2sin(![]() ﹣
﹣![]() ) D.y=2sin(2x﹣
) D.y=2sin(2x﹣![]() )
)
最近更新
- 26.报春花的花色白色(只含白色素)和黄色(含黄色锦葵色素)由两对等位基因(A和a,B和b)共同控制,两对等位基因独立遗
- 请根据下列提示,用英语为某品牌一款智能手机写一篇促销说明 必要性:手机是人们联系工具之一 颜色:各种颜色可供选择
- 如图9,用磁铁的一极在钢棒AB上从A向B反复摩擦几次后,钢棒就具有了磁性,这种现象称为 ,并且钢棒的A端为极。
- 取1~5号五支试管,分别加入2 mL 0.5 mol/L的过氧化氢溶液,进行如下实验: 试管编号 1 2 3 4 5 加
- 下列电子式,正确的是( )
- T appreciate that it's not easy for you, but you ______ try
- 下列离子方程式的书写正确的是() A.铁与稀硫酸反应:2Fe+6H+=2Fe3++3H2↑ B.硫酸铜溶液跟氢氧化钡
- 青藏地区气候的主要特点是: A.光照强烈 B.干旱少雨 C.昼夜温差大 D.寒冷
- 已知等差数列{an}的前n项和为Sn,且a3+a6=4,S5=-5. (1)求数列{an}的通项公式; (2)若Tn=|
- 酚酞的结构简式如图,下列关于酚酞的说法一定正确的是A. 酚酞的分子式是C20H12O4 B. 分子中的碳原子不在同一平面
- 0.2 mol有机物和0.4 mol O2在密闭容器中燃烧后的产物为CO2、CO和H2O(g)。产物经过浓硫酸后,浓硫酸
- 已知2x+y=0是双曲线x2-λy2=1的一条渐近线,则双曲线的离心率为( )A. B.
- 已知NH3和Cl2可快速反应:2NH3+3Cl2====N2+6HCl 图1-6为反应后总体积V(L)随原混合气体中Cl
- —Wouldyou like to go out for a meal with me tonight? —___
- 往AgNO3和Cu(NO3)2的混合溶液中加入一定量的铁粉,充分反应后过滤,向滤渣中加入稀盐酸,无气泡产生.根据上述现象
- 太阳辐射是太阳以电磁波的形式向宇宙空间放射的能量。请回答下列各题。 有关太阳辐射及其对地球影响的叙述,不正确的是(
- (本题满分16分) 随机抽取某厂的某种产品200件,经质检,其中有一等品126件、二等品50件、三等品20件、次品4件.
- 下列词语中加点的字,读音全部正确的一项是 A、埋怨(mái) 接榫(sǔn) 翘首(qiáo)
- 2009年3月25日国务院常务会议审议并原则通过关于推进上海加快发展现代服务业和先进制造业、建设国际金融中心和国际航运中
- 下列各组句子中,加点的词的意义和用法不相同的一组是( ) A.是吾俸禄之余,故以为汝粮耳。 见其客朱亥,