高中 数学
已知函数  .
.
 .
.
-
(1) 求函数
 的单调区间,并求
的单调区间,并求  的最值;
的最值;
-
(2) 已知
 ,
,  .
. ①证明:
 有最小值;
有最小值;②设
 的最小值为
的最小值为  ,求函数
,求函数  的值域.
的值域.
已知正方体  棱长为2,
棱长为2, 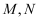 为体对角线
为体对角线  上的两动点,且
上的两动点,且  ,动点
,动点  在三角形
在三角形  内,且三角形
内,且三角形  的面积
的面积  ,则点
,则点  的轨迹长度为.
的轨迹长度为.
 棱长为2,
棱长为2, 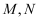 为体对角线
为体对角线  上的两动点,且
上的两动点,且  ,动点
,动点  在三角形
在三角形  内,且三角形
内,且三角形  的面积
的面积  ,则点
,则点  的轨迹长度为.
的轨迹长度为. 
已知正实数  满足
满足  ,那么
,那么  的最大值是.
的最大值是.
 满足
满足  ,那么
,那么  的最大值是.
的最大值是.
已知  ,数列
,数列  前
前  项和为
项和为  ,且
,且  .
.
 ,数列
,数列  前
前  项和为
项和为  ,且
,且  .
.
-
(1) 求数列
 的通项公式
的通项公式  ;
;
-
(2) 若数列
 满足
满足  ,数列
,数列  的前
的前  项和为
项和为  ,且对于任意
,且对于任意  ,总存在
,总存在  ,使得
,使得  成立,求实数
成立,求实数  的取值范围.
的取值范围.
复数 , 且A+B=0,则m=( )
, 且A+B=0,则m=( )
 , 且A+B=0,则m=( )
, 且A+B=0,则m=( )
A .  B .
B .  C .
C .  D . 2
D . 2
 B .
B .  C .
C .  D . 2
D . 2
下列不等式中:
①  ;②
;②  ;③
;③  ;④
;④  .其中正确的序号是( )
.其中正确的序号是( )
A . ①②③④
B . ①②③
C . ①②④
D . ③④
已知cos(  +φ)=
+φ)=  且 |φ|<
且 |φ|<  ,则tanφ等于 ( )
,则tanφ等于 ( )
 +φ)=
+φ)=  且 |φ|<
且 |φ|<  ,则tanφ等于 ( )
,则tanφ等于 ( )
A . -  B . -
B . -  C .
C .  D .
D . 
 B . -
B . -  C .
C .  D .
D . 
某种产品投放市场以来,通过市场调查,销量t(单位:吨)与利润Q(单位:万元)的变化关系如右表,现给出三种函数  ,
,  ,
,  且
且  ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
 ,
,  ,
,  且
且  ,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量.
,请你根据表中的数据,选取一个恰当的函数,使它能合理描述产品利润Q与销量t的变化,求所选取的函数的解析式,并求利润最大时的销量. | 销量t | 1 | 4 | 6 |
| 利润Q | 2 | 5 | 4.5 |
已知双曲线  的一条渐近线的方程为
的一条渐近线的方程为 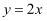 ,则
,则  .
.
 的一条渐近线的方程为
的一条渐近线的方程为 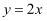 ,则
,则  .
.
 ,若
,若  ,则
,则  =( )
=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知等差数列  满足
满足  ,
,  ,
,  .
.
 满足
满足  ,
,  ,
,  .
.
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 若数列
 满足
满足  ,
,  ,求数列
,求数列  的前
的前  项和.
项和.
已知函数  .
.
 .
.
-
(1) 求函数
 的单调递增区间;
的单调递增区间;
-
(2) 将
 的图像向左平移
的图像向左平移  个单位长度,再将得到的图像横坐标变为原来的2倍(纵坐标不变),得到
个单位长度,再将得到的图像横坐标变为原来的2倍(纵坐标不变),得到  的图像.若函数
的图像.若函数  在区间
在区间  上的图像与直线
上的图像与直线  有三个交点,求实数
有三个交点,求实数  的取值范围.
的取值范围.
命题“  ,
,  ”的否定为( )
”的否定为( )
 ,
,  ”的否定为( )
”的否定为( )
A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
在等边  中,点
中,点  在中线
在中线  上,且
上,且  ,则
,则  ( )
( )
 中,点
中,点  在中线
在中线  上,且
上,且  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在平行六面体 中,
中, 为
为 与
与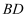 的交点,若
的交点,若 ,
,  ,
,  , 则下列向量运算不正确的是( )
, 则下列向量运算不正确的是( )
 中,
中, 为
为 与
与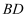 的交点,若
的交点,若 ,
,  ,
,  , 则下列向量运算不正确的是( )
, 则下列向量运算不正确的是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设实数  满足
满足  ,则
,则  的最小值为.
的最小值为.
 满足
满足  ,则
,则  的最小值为.
的最小值为.
根据中国海洋生态环境状况公报,从2017年到2021年全国直排海污染物中各年份的氨氮总量y(单位:千吨)与年份的散点图如下:

记年份代码为 ,
,  , 对数据处理后得:
, 对数据处理后得:
|
|
|
|
|
|
6 | 0.45 | 1.5 | 210 | 76 | 17 |
-
(1) 根据散点图判断,模型①
 与模型②
与模型② 哪一个适宜作为y关于x的回归方程?(给出判断即可,不必说明理由)
哪一个适宜作为y关于x的回归方程?(给出判断即可,不必说明理由)
-
(2) 根据(1)的判断结果,建立y关于x的回归方程,并预测2022年全国直排海污染物中的氨氮总量(计算结果精确到0.01).
参考公式:回归方程
 中斜率和截距的最小二乘估计公式分别为:
中斜率和截距的最小二乘估计公式分别为: ,
,  .
.
在直角坐标系中,求点(2x+3-x2,![]() )在第四象限的充要条件.
)在第四象限的充要条件.
设a=log23,b![]() ,c=e
,c=e![]() ,则a,b,c的大小关系是
,则a,b,c的大小关系是
A.a<b<c B.b<a<c C.b<c<a D.a<b<c
已知![]()
![]() ,则
,则![]() 的最小值为 ( )
的最小值为 ( )
A.12 B.15 C.![]() D.
D.![]()
A. ![]() 的周期为4 B.
的周期为4 B. ![]() 是奇函数 C.
是奇函数 C. ![]() D.
D. ![]() 是奇函数
是奇函数
最近更新
- 化学就在我们身边,我们的生活离不开化学物质。现有以下几种物质:①液氧 ②稀有气体 ③水 ④干冰,请选择适当的物质用
- 测量滑块在运动过程中所受的合外力是“探究动能定理”实验要解决的一个重要问题。为此,某同学设计了如下实验方案:A.实验装置
- ----- ________doyou visit your grandparents? -------O
- 下列说法不正确的是( ) A.麦芽糖及其水解产物均能发生银镜反应 B.用溴水即可鉴别苯酚溶液、2,4己二烯和甲
- The road for vehicles is under repair.Drivers are re
- 下面语段中有两个病句,请把它们找出来,并加以改正。(2分) ①今年全国将有10个省、市、自治区试点在音乐课程中增加京剧内
- —Why do you look so blue? —The mosquitoes ________me so much
- 下列词语中加线的字的注音,全都正确的一组是( ) A.桀骜(ào ) 喋血(dié ) 浸渍(zì) 殒身不恤(xié)
- 过点 引直线 与圆 相交于 两点, 为坐标原点,当 面积取最大值时,直线 的斜率为 ( ) A. B. C.
- 生物界的生物形形色色、多种多样的根本原因是( ) A.蛋白质分子结构的多样性 B.DN
- 实验中用35S标记一定量的氨基酸,来培养某哺乳动物的乳腺细胞,测得与合成和分泌乳蛋白相关的一些细胞器上放射性强度的变化曲
- 下列各组化合物中,化学键类型完全相同的是() A.C2H6、H2O2、C2H5OH B.HCl
- 下列实验操作中正确的是: A.分液时,分液
- 燕麦幼苗产生生长素部位、感受光刺激部位、向光弯曲部位依次为胚芽鞘的( ) A.尖端、尖端下面的一段、基部 B.尖端
- 下列各句中,没有语病的一项是 A. 我看古今中外,在文学语言的运用上,都不能离开这一条:刻苦的选择和严格的追求。 B.
- 某溶液中可能存在Mg2+、Fe2+、Fe3+,加入NaOH溶液,开始时有白色絮状沉淀,迅速变成灰绿色,最后变成红褐色,下
- 函数和在第一象限内的图象如图,点P是的图象上一动点,PC⊥x轴于点C,交的图象于点A,PD⊥y轴于D,交的图象于点B,给
- 同宗教界“政治上团结合作,信仰上互相尊重”,是中国始终坚持的原则。同宗教界之所以能够团结合作,是因为() A.我国宗
- A recent study, published in lastweek’s Journal of the
- 手足口病是一种常见多发传染病,以婴幼儿发病为主,主要通过接触病人的粪便、疱疹液和呼吸道分泌物及被污染的手、毛巾、手绢、玩









