高中 数学
在等差数列  中,若
中,若  ,则
,则  ,
,  .
.
 中,若
中,若  ,则
,则  ,
,  .
.
)一个几何体的三视图如图所示(单位:m),则该几何体的表面积为(单位:m2)( )

A . (11+4 )π
B . (12+4
)π
B . (12+4 )π
C . (13+4
)π
C . (13+4 )π
D . (14+4
)π
D . (14+4 )π
)π
 )π
B . (12+4
)π
B . (12+4 )π
C . (13+4
)π
C . (13+4 )π
D . (14+4
)π
D . (14+4 )π
)π
解关于x的方程:

下列判断正确的是( )
A . 线性回归直线  必经过点
必经过点  ,
,  ,…
,…  中心点
中心点  B . 从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C . 若两个随机变量的线性相关性越强,则相关系数
B . 从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C . 若两个随机变量的线性相关性越强,则相关系数  的绝对值越接近于1
D . 将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
的绝对值越接近于1
D . 将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
 必经过点
必经过点  ,
,  ,…
,…  中心点
中心点  B . 从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C . 若两个随机变量的线性相关性越强,则相关系数
B . 从独立性检验可知有99%的把握认为吃地沟油与患胃肠癌有关系时,我们就说如果某人吃地沟油,那么他有99%可能患胃肠癌
C . 若两个随机变量的线性相关性越强,则相关系数  的绝对值越接近于1
D . 将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
的绝对值越接近于1
D . 将一组数据的每一个数据都加上或减去同一个常数后,其方差也要加上或减去这个常数
设函数  ,则满足
,则满足  的
的  的取值范围是.
的取值范围是.
 ,则满足
,则满足  的
的  的取值范围是.
的取值范围是.
直线x﹣y+4=0被圆(x+2)2+(y﹣2)2=2截得的弦长等于( )
A . 12 B . 2
B . 2 C . 3
C . 3 D . 4
D . 4
 B . 2
B . 2 C . 3
C . 3 D . 4
D . 4
已知向量  =(2,3),
=(2,3),  =(﹣1,2),若m
=(﹣1,2),若m  +
+  与
与  ﹣2
﹣2  平行,则m等于.
平行,则m等于.
 =(2,3),
=(2,3),  =(﹣1,2),若m
=(﹣1,2),若m  +
+  与
与  ﹣2
﹣2  平行,则m等于.
平行,则m等于.
将1000名学生的编号如下:0001,0002,0003,…,1000,若从中抽取50个学生,用系统抽样的方法从第一部分0001,0002,…,0020中抽取的号码为0015时,抽取的第40个号码为( )
A . 0795
B . 0780
C . 0810
D . 0815
在△ABC中,a、b、c分别是角A、B、C的对边,△ABC的面积为S,(a2+b2)tanC=8S,则  =.
=.
 =.
=.
已知椭圆的方程为  ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
 ,则此椭圆的离心率为( )
,则此椭圆的离心率为( )
A . 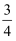 B .
B . 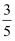 C .
C . 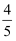 D .
D . 
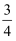 B .
B . 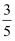 C .
C . 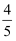 D .
D . 
若函数f(x)满足对于任意实数a,b,c,都有f(a),f(b),f(c)为某三角形的三边长,则成f(x)为“可构造三角形函数”,已知f(x)=  是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
 是“可构造三角形函数”,则实数t的取值范围是( )
是“可构造三角形函数”,则实数t的取值范围是( )
A . [﹣1,0]
B . (﹣∞,0]
C . [﹣2,﹣1]
D . [﹣2,﹣  ]
]
 ]
]
函数  ,则( )
,则( )
 ,则( )
,则( )
A . 在  上递增;
B . 在
上递增;
B . 在  上递减;
C . 在
上递减;
C . 在  上递增;
D . 在
上递增;
D . 在  上递减
上递减
 上递增;
B . 在
上递增;
B . 在  上递减;
C . 在
上递减;
C . 在  上递增;
D . 在
上递增;
D . 在  上递减
上递减
如图,在四棱锥  中,
中,  为等边三角形,平面
为等边三角形,平面  平面CDE,
平面CDE,  ,二面角
,二面角  的大小为60º.
的大小为60º.
 中,
中,  为等边三角形,平面
为等边三角形,平面  平面CDE,
平面CDE,  ,二面角
,二面角  的大小为60º.
的大小为60º. 
-
(1) 求证:
 平面ABE;
平面ABE;
-
(2) 若
 ,点
,点  为线段AB上的点,若直线
为线段AB上的点,若直线 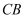 与平面
与平面  所成角的正弦值为
所成角的正弦值为  ,求线段
,求线段  的长度.
的长度.
在△ABC中,若|  +
+  |=|
|=|  ﹣
﹣  |,AB=2,AC=1,E,F为BC边的三等分点,则
|,AB=2,AC=1,E,F为BC边的三等分点,则  •
•  =( )
=( )
 +
+  |=|
|=|  ﹣
﹣  |,AB=2,AC=1,E,F为BC边的三等分点,则
|,AB=2,AC=1,E,F为BC边的三等分点,则  •
•  =( )
=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
《中国制造2025》是经国务院总理李克强签批,由国务院于2015年5月印发的部署全面推进实施制造强国的战略文件,是中国实施制造强国战略第一个十年的行动纲领.制造业是国民经济的主体,是立国之本、兴国之器、强国之基.发展制造业的基本方针为质量为先,坚持把质量作为建设制造强国的生命线.某制造企业根据长期检测结果,发现生产的产品质量与生产标准的质量差都服从正态分布N(μ,σ2),并把质量差在(μ﹣σ,μ+σ)内的产品为优等品,质量差在(μ+σ,μ+2σ)内的产品为一等品,其余范围内的产品作为废品处理.优等品与一等品统称为正品.现分别从该企业生产的正品中随机抽取1000件,测得产品质量差的样本数据统计如下:

-
(1) 根据频率分布直方图,求样本平均数

-
(2) 根据大量的产品检测数据,检查样本数据的方差的近似值为100,用样本平均数
 作为μ的近似值,用样本标准差s作为σ的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表)
作为μ的近似值,用样本标准差s作为σ的估计值,求该厂生产的产品为正品的概率.(同一组中的数据用该组区间的中点值代表) [参考数据:若随机变量ξ服从正态分布N(μ,σ2),则:P(μ﹣σ<ξ≤μ+σ)≈0.6827,P(μ﹣2σ<ξ≤μ+2σ)≈0.9545,P(μ﹣3σ<ξ≤μ+3σ)≈0.9973.
-
(3) 假如企业包装时要求把3件优等品球和5件一等品装在同一个箱子中,质检员每次从箱子中摸出三件产品进行检验,记摸出三件产品中优等品球的件数为X,求X的分布列以及期望值.
已知正实数  满足
满足  ,则
,则  的最小值为.
的最小值为.
 满足
满足  ,则
,则  的最小值为.
的最小值为.
设函数  ,其中
,其中  表示不超过
表示不超过  的最大整数,如
的最大整数,如  ,
,  ,
,  ,若直线
,若直线  与函数
与函数  的图象恰有三个不同的交点,则
的图象恰有三个不同的交点,则  的取值范围是( )
的取值范围是( )
 ,其中
,其中  表示不超过
表示不超过  的最大整数,如
的最大整数,如  ,
,  ,
,  ,若直线
,若直线  与函数
与函数  的图象恰有三个不同的交点,则
的图象恰有三个不同的交点,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
曲线y=3(x2+x)ex在点(0,0)处的切线方程为 .
函数![]() =
=![]() 的单调减区间为( )
的单调减区间为( )
A. (![]() ) B. (
) B. (![]() ) C. (
) C. (![]() ) D. (0,
) D. (0, ![]() )
)
如图,在长方体 中,
中, ,
, ,则四棱锥
,则四棱锥 的体积为 ▲ cm3.
的体积为 ▲ cm3.

最近更新
- 唐诗载:“自从贵主和亲后,一半胡风似汉家”,正确反映了 A.吐蕃强大的原因 B.吐
- 甲乙两辆汽车在平直的公路上沿同一方向做直线运动,t=0时刻同时经过公路旁的同一个路标在如图描述两车运动的v – t 图中
- 某质点的位移随时间的变化关系式为x=4t+2t2,x与t的单位分别是米与秒,则质点的初速度与加速度分别是A.4m/s与2
- 我国社会主义仍然处于初级阶段的表现有 ①社会生产力水平还比较低 ②科学技术水平、
- 有可逆反应A+B2C在不同温度下经过一定时间,混合物中C的百分含量与温度关系如下图所示,那么:(1)反应在_______
- 下列关于石油的叙述不正确的是A.石油是一种化工产品 B.石油是一种混合物C.可利用石油产
- 在马克思的墓碑上刻着两行字:“以往的哲学家只是解释世界,而问题在于改造世界。”这说明马克思主义哲学坚持( ) A.
- (本题满分10分)已知数列的前项和为,通项公式为,.(Ⅰ)计算的值;(Ⅱ)比较与1的大小,并用数学归纳法证明你的结论.
- 某发电站的输出功率为104kW,输出电压为4kV,通过理想变压器升压后向80km远处供电。已知输电导线的电阻R=25.6
- 资产阶级革命战争或改革完成后,英、法、美、德各国先后建立了形式各异的资产阶级民主制度,但核心都是由议会掌握了国家的 A.
- 在R上可导的函数f(x)的图象如图示,f(x)为函数f(x)的导数,则关于x的不等式x•f(x)<0的解集为()A.
- (2008·山东威海教学质量检测)中俄双方就黑瞎子岛归属问题,进行了长达40余年的谈判。期间也发生过不少冲突,但我国始终
- 如图所示是日光灯的结构示意图,若按图示的电路连接,关于日光灯发光的情况,下列叙述中正确的是( )A.S1接通,S2、S3
- 已知在1×105 Pa,298 K条件下,2 mol氢气燃烧生成水蒸气放出484 kJ热量,下列热化学方程式正确的是(
- 对于20世纪三四十年代苏联的某种政治经济模式,有学者认为:从富国强兵的角度来说,成绩是辉煌的,但从社会的全面发展来说,是
- 读下图,阴影部分表示黑夜,回答问题。(l)按此图所示,北京时间为________;地方时为0点的经线所属的时区为____
- She may have missed the train,____ she won’t arrive for anot
- 已知f(x)=则不等式x+(x+2)·f(x+2)≤5的解集是_______________.
- 1929—1933年资本主义世界经济危机首先爆发于 A.工业生产领域 B.农业生
- 如图所示,长为的细线一端固定在O点,另一端拴一质量为m的小球,现使小球恰好能在竖直平面内做完整的圆周运动,已知O点到水平



