高中 数学
某几何体的三视图如图所示,则该几何体的体积为( )

A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
-
(1)
 ;
;
-
(2)
 .
.
下列对动直线 的四种表述不正确的是( )
的四种表述不正确的是( )
 的四种表述不正确的是( )
的四种表述不正确的是( )
A . 与曲线C: 可能相离,相切,相交
B . 恒过定点
可能相离,相切,相交
B . 恒过定点 C .
C .  时,直线斜率是0
D .
时,直线斜率是0
D . 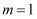 时,直线的倾斜角是135°
时,直线的倾斜角是135°
 可能相离,相切,相交
B . 恒过定点
可能相离,相切,相交
B . 恒过定点 C .
C .  时,直线斜率是0
D .
时,直线斜率是0
D . 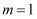 时,直线的倾斜角是135°
时,直线的倾斜角是135°
在平面直角坐标系中,若点P(x,y)的坐标x,y均为整数,对称点P为格点.若一个多边形的顶点全是格点,则称该多边形为格点多边形.格点多边形的面积记为S,其内部的格点数记为N.边界上的格点数记为L.例如图中△ABC是格点三角形,对应的S=1,N=0,L=4.

-
(1) 图中格点四边形DEFG对应的S,N,L分别是.
-
(2) 已知格点多边形的面积可表示为S=aN+bL+c,其中a,b,c为常数,若某格点多边形对应的N=17,L=10,则S=(用数值作答).
如图是某校高三某班甲、乙两位同学前六次模拟考试的数学成绩,则下列判断正确的是( )

A .  ,甲比乙成绩稳定
B .
,甲比乙成绩稳定
B .  ,乙比甲成绩稳定
C .
,乙比甲成绩稳定
C .  ,甲比乙成绩稳定
D .
,甲比乙成绩稳定
D .  ,乙比甲成绩稳定
,乙比甲成绩稳定
 ,甲比乙成绩稳定
B .
,甲比乙成绩稳定
B .  ,乙比甲成绩稳定
C .
,乙比甲成绩稳定
C .  ,甲比乙成绩稳定
D .
,甲比乙成绩稳定
D .  ,乙比甲成绩稳定
,乙比甲成绩稳定
设函数f(x)=  ,则f(f(2))=( )
,则f(f(2))=( )
 ,则f(f(2))=( )
,则f(f(2))=( )
A .  B . 16
C .
B . 16
C .  D . 4
D . 4
 B . 16
C .
B . 16
C .  D . 4
D . 4
某工厂制作如图所示的一种标识,在半径为R的圆内做一个关于圆心对称的“工”字图形,“工”字图形由横、竖、横三个等宽的矩形组成,两个横距形全等且成是竖矩形长的 倍,设O为圆心,∠AOB=2α,“工”字图形的面积记为S.
倍,设O为圆心,∠AOB=2α,“工”字图形的面积记为S.
 倍,设O为圆心,∠AOB=2α,“工”字图形的面积记为S.
倍,设O为圆心,∠AOB=2α,“工”字图形的面积记为S.将S表示为α的函数.

若a是f(x)=sinx﹣xcosx在x∈(0,2π)的一个零点,则∀x∈(0,2π),下列不等式恒成立的是( )
A .  B . cosa≥
B . cosa≥ C .
C .  ≤a≤2π
D . a﹣cosa≥x﹣cosx
≤a≤2π
D . a﹣cosa≥x﹣cosx
 B . cosa≥
B . cosa≥ C .
C .  ≤a≤2π
D . a﹣cosa≥x﹣cosx
≤a≤2π
D . a﹣cosa≥x﹣cosx
在平面四边形  中,
中,  ,
,  ,将
,将  沿
沿  折起,使得平面
折起,使得平面  平面
平面  ,如图.
,如图.
 中,
中,  ,
,  ,将
,将  沿
沿  折起,使得平面
折起,使得平面  平面
平面  ,如图.
,如图. 
-
(1) 求证:
 ;
;
-
(2) 若
 为
为  中点,求直线
中点,求直线  与平面
与平面  所成角的正弦值.
所成角的正弦值.
统计某校400名学生的数学会考成绩,得到样本频率分布直方图,规定不低于80分为优秀,则优秀人数为人.(注:每组包含最小值不包含最大值,且数学会考成绩均为整数)

在复平面内,复数  对应的点位于( )
对应的点位于( )
 对应的点位于( )
对应的点位于( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
已知一组观测值具有线性相关关系,若对于 , 求得
, 求得 , 则线性回归方程是( )
, 则线性回归方程是( )
 , 求得
, 求得 , 则线性回归方程是( )
, 则线性回归方程是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知  ,函数
,函数  在
在  上单调递减,则
上单调递减,则 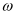 的取值范围是
的取值范围是 

 ,函数
,函数  在
在  上单调递减,则
上单调递减,则 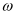 的取值范围是
的取值范围是 

A .  B .
B .  C .
C .  D .
D . 
正方体ABCD﹣A1B1C1D1中直线BC1与平面BB1D1D所成角的余弦值是
若函数f(x)=x2﹣2x+1在区间[a,a+2]上的最小值为4,则a的取值集合为( )
A . [﹣3,3]
B . [﹣1,3]
C . {﹣3,3}
D . [﹣1,﹣3,3]
若sin ![]() -2cos
-2cos ![]() =0,则tan θ=________.
=0,则tan θ=________.
(本小题满分12分)
已知![]() 且
且![]() ,
,
(1)求![]() 最小值
最小值![]() ;
;
(2)求![]() 的最小值
的最小值
设△ABC的内角A,B,C的对边分别为a,b,c,且a=2![]() ,cosC=-
,cosC=-![]() ,3sinA=2sinB,则c=__________.
,3sinA=2sinB,则c=__________.
已知曲线![]() 的极坐标方程为
的极坐标方程为![]() ,
,![]() 的参数方程为
的参数方程为 (
(![]() 为参数).
为参数).
(1)将曲线![]() 与
与![]() 的方程化为直角坐标系下的普通方程;
的方程化为直角坐标系下的普通方程;
(2)若![]() 与
与![]() 相交于
相交于![]() 两点,求
两点,求![]() .
.
如果等差数列![]() 中,
中,![]() ,那么
,那么![]()
A. 14 B.21 C.28 D.35
最近更新
- 古诗云“黄河之水天上来”,“百川归大海,何日复西归”。根据两句诗句回答18-19题。 18.从河水补给角度看,“黄河之水
- (08年天津南开区质检一理)(12分)已知函数。(1)若函数的导函数是奇函数,求的值;(2)求函数的单调区间。
- 阅读下面两则材料,回答问题。 材料一:近年来清明节祭奠亲友,一些地方从烧冥钞、纸人、纸马,发展到烧纸电视机、纸数码相机,
- There _________some water in the bottle. A. is B.are
- 写出一个图象位于第一、三象限的反比例函数的表达式: .
- 分子式为C5H12O的醇,能被氧化成醛的同分异构体有( ) A.4种 B.5种
- 有关食物的消化和吸收的下列叙述中,错误的是() A.口腔能对淀粉起初步消化作用 B.胃蛋白酶能对蛋白质起初步消化的作用
- One day my teacher said, “ Life is a game of chess, a
- 世界杯决赛中,德国队在加时赛中踢进了全场唯一一个进球,第四次捧起了大力神杯。德国球迷看到这一幕时欢呼雀跃、心跳加快、血压
- 鸡蛋壳的主要成分是碳酸钙,为了测定某鸡蛋壳中碳酸钙的含量,小群同学进行了如下实验:将鸡蛋壳洗净、干燥并捣碎后,称取10g
- 美国一位历史学家说“的大多数领导人被蒋介石杀害,但有些人逃进了华南山区。他们的领导人之一是,这时无视莫斯科的第三国际,制
- It is certain that he will__________ his business to his son
- 在温度一定的条件下,做“研究决定电阻大小因素”的实验时,采用了_______的方法,即每次选用两根合适的导线,测
- 香港创新科技署署长在香港电子科技商会2009周年晚宴上表示: 在这次金融风暴中体验到,从事高增值高科技的企业,一般比其它
- 斯塔夫里阿诺斯指出:“铁制工具还促进了在黄河流域地区兴修大批的排水工程,为远距离运输大批商品而进行的运河开挖以及在西北干
- 2008年是我国改革开放的第30年。改革开放以来我们取得一切成绩和进步的根本原因,归结起来就是:开辟了中国特色社会主义道
- (本题满分12分) 已知函数,求 求的最小正周期及对称中心; 当时,求的最大值和最小值.
- (03年江苏卷)设函数的取值范围是( ) (A)(-1,1)
- 下列关于各实验装置的叙述正确的是 A.装置①可用于收集C2H4、HCl、SO2等气体 B.装置
- 在庆祝十月革命40周年时,赫鲁晓夫提出在15年内在人均产品产量赶上和超过美国。1961年他又声称苏联将在“20年内基本建



