高中 数学
过点  的圆
的圆  的切线方程为.
的切线方程为.
 的圆
的圆  的切线方程为.
的切线方程为.
数列  是等差数列,
是等差数列,  ,
,  ,则
,则  ( )
( )
 是等差数列,
是等差数列,  ,
,  ,则
,则  ( )
( )
A . 12
B . 24
C . 36
D . 72
设 是给定的平面,
是给定的平面,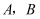 是不在
是不在 内的任意不同的两点,则( )
内的任意不同的两点,则( )
 是给定的平面,
是给定的平面,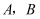 是不在
是不在 内的任意不同的两点,则( )
内的任意不同的两点,则( )
A . 在 内存在直线与直线AB平行
B . 在
内存在直线与直线AB平行
B . 在 内存在直线与直线AB垂直
C . 存在过直线AB的平面与
内存在直线与直线AB垂直
C . 存在过直线AB的平面与 平行
D . 存在过直线AB的平面与
平行
D . 存在过直线AB的平面与 垂直
垂直
 内存在直线与直线AB平行
B . 在
内存在直线与直线AB平行
B . 在 内存在直线与直线AB垂直
C . 存在过直线AB的平面与
内存在直线与直线AB垂直
C . 存在过直线AB的平面与 平行
D . 存在过直线AB的平面与
平行
D . 存在过直线AB的平面与 垂直
垂直
2log510+log50.25=
方程  表示双曲线的一个充分不必要条件是( )
表示双曲线的一个充分不必要条件是( )
 表示双曲线的一个充分不必要条件是( )
表示双曲线的一个充分不必要条件是( )
A .  B .
B .  或
或  C .
C .  D .
D . 
 B .
B .  或
或  C .
C .  D .
D . 
设 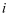 为虚数单位,若复数
为虚数单位,若复数  满足
满足  ,则复数
,则复数  ( )
( )
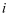 为虚数单位,若复数
为虚数单位,若复数  满足
满足  ,则复数
,则复数  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  满足
满足  ,当
,当  时,
时,  ,且
,且  .
.
 满足
满足  ,当
,当  时,
时,  ,且
,且  .
.
-
(1) 求
 的值,并判断
的值,并判断  的单调性;
的单调性;
-
(2) 当
 时,不等式
时,不等式  恒成立,求实数
恒成立,求实数  的取值范围.
的取值范围.
设 , 则“
, 则“ ”是“
”是“ ”( )
”( )
 , 则“
, 则“ ”是“
”是“ ”( )
”( )
A . 充分而不必要条件
B . 必要而不充分条件
C . 充分必要条件
D . 既不充分也不必要条件
已知直线kx﹣y=k﹣1与ky﹣x=2k的交点在第二象限,则实数k的取值范围是( )
A . (0, )
B . (
)
B . ( , 1)
C . (0,1)
D . [1]
, 1)
C . (0,1)
D . [1]
 )
B . (
)
B . ( , 1)
C . (0,1)
D . [1]
, 1)
C . (0,1)
D . [1]
如图所示,在多面体ABCDEF中,四边形ADEF为正方形,AD∥BC,AD⊥AB,AD=2BC=1.

-
(1) 证明:平面ADEF⊥平面ABF.
-
(2) 若AF⊥平面ABCD,二面角A-BC-E为30°,三棱锥A-BDF的外接球的球心为O,求二面角A-CD-O的余弦值.
函数y=2sin(2x﹣  )与y轴最近的对称轴方程是.
)与y轴最近的对称轴方程是.
 )与y轴最近的对称轴方程是.
)与y轴最近的对称轴方程是.
函数  的图象如图所示,则
的图象如图所示,则  的表达式是( )
的表达式是( )
 的图象如图所示,则
的图象如图所示,则  的表达式是( )
的表达式是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在平面直角坐标系中,曲线  的参数方程为
的参数方程为  (
(  为参数).以原点
为参数).以原点  为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线  的极坐标为
的极坐标为 
 的参数方程为
的参数方程为  (
(  为参数).以原点
为参数).以原点  为极点,
为极点,  轴的非负半轴为极轴建立极坐标系,直线
轴的非负半轴为极轴建立极坐标系,直线  的极坐标为
的极坐标为 
-
(1) 求曲线
 的普通方程与直线
的普通方程与直线  的直角坐标方程;
的直角坐标方程;
-
(2) 设直线
 与曲线
与曲线  交于
交于  两点,点
两点,点  的坐标为
的坐标为  ,证明:直线
,证明:直线  关于
关于  轴对称.
轴对称.
已知数列{an}的前n项和Sn=﹣an﹣(  )n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
)n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
 )n﹣1+2(n∈N*),数列{bn}满足bn=2nan .
)n﹣1+2(n∈N*),数列{bn}满足bn=2nan . (Ⅰ)求证数列{bn}是等差数列,并求数列{an}的通项公式;
(Ⅱ)设cn=log2  ,数列{
,数列{  }的前n项和为Tn , 求满足Tn
}的前n项和为Tn , 求满足Tn  (n∈N*)的n的最大值.
(n∈N*)的n的最大值.
椭圆![]() 中,
中,![]() 成等比数列,椭圆的离心率为
成等比数列,椭圆的离心率为![]() 双曲线
双曲线![]() 中,
中,![]() 成等比数列,双曲线的离心率为
成等比数列,双曲线的离心率为![]() 则
则![]() .
.
若????,y满足![]() ,则2y−????的最小值是_________.
,则2y−????的最小值是_________.
已知平面向量![]() ,
,![]() 满足
满足![]() ,
,![]() ,
,![]() 与
与![]() 的夹角为
的夹角为![]() ,若
,若![]() ,则实数
,则实数![]() 的值为
的值为
A. ![]() B.
B.![]()
C.![]() D.
D. ![]()
一个人打靶时连续射击两次,事件“至少有一次中靶”的互斥事件是
A.至多有一次中靶 B.两次都中靶
C.只有一次中靶 D.两次都不中靶
.设![]() ,则有( )
,则有( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
函数y=![]() 的定义域是 ( )
的定义域是 ( )
A . {x|x>0} B . {x|x≥1} C .{x|x≤1} D.{x|0<x≤1}
最近更新
- 体积为1 L的干燥容器中充入HCl气体后,测得容器中气体对氧气的相对密度为1.082。将此气体倒扣在水中,进入容器中液体
- 下列各句中没有通假字的一项是 A、乃瞻衡宇,载欣载奔。 B、此小大之辩也。 C、定乎内外之分,辩乎荣
- 句型转换。根据要求变换句型,每空填一词。 92.Is this a ruler? (作否定回答) No, _______
- Taking goodnotes is a time-saving skill that will help you t
- 下列句子中,没有语病的一项是 () A.青少年是上网人群中的主力军,但最近几年,在发达国家
- 所有小于3.14的非负整数是 ,不小于−3并且小于2的整数是 .
- 下列四个地区中,农业生产部门以畜牧业为主的是 ( )A、辽东丘
- 荀子日:“蓬生麻中,不扶自直;白沙在涅,与之俱黑。”从文化对人影响的角度看,下列说法体现的道理与之不一致的是 A.
- 地球上的水圈是一个() A.不连续、有规则的圈层 B.连续的、不规则的圈层 C.连续的、有规则的圈层 D.不连续
- 有人做了如下试验,迅速将一只椿象杀死,尽管做得悄无声息,也能引起其它椿象的逃逸。椿象间的联系方式是( ) A 椿象发出
- Either you or the headmaster ______ the prizes to students a
- (8分) 解方程:
- 下列物质能使品红溶液褪色,且褪色原理基本相同的组合是() ①活性炭 ②氯水 ③二氧化硫 ④臭氧 ⑤过氧化钠 ⑥双氧水 A
- I can’t help _____repairs because I’ve something important _
- 已知1、2、3、的平均数是8,那么的值是 ( ) A 14 B 22 C 32
- (三)名篇名句默写(5分) 16.补写出下列名篇名句中的空缺部分。 (1)《劝学》指出“青取之于蓝,而青于蓝”,这与《师
- 下列各句中,加点的成语使用恰当的一句是:A. 儒道思想之争的结果使得中国古代的读书人大都秉持一套及其圆滑的哲学:达则兼济
- 下列有关南极地区及科考站的叙述,正确的是 A.我国的三个科学考察站均有极昼极夜现象 B.南极地区的典型动物是企鹅和北极熊
- —May I speak to Miss Wang?—Sorry. She isn’t in. She ________
- Obama was elected president of the USA is a big succ



