高中 数学
 平面ABCD,
平面ABCD,  ,
,  ,
,  .
. 
-
(1) 求直线PD与平面PCE所成角的正弦值;
-
(2) 在棱AB上是否存在一点F,使得二面角E-PC-F的大小为60°?如果存在,确定点F的位置;如果不存在,说明理由.
 ,则集合
,则集合  的元素个数为( )
的元素个数为( ) B .
B .  C .
C .  D .
D . 
 上的C点出发,经该扇形半径两次反射用时
上的C点出发,经该扇形半径两次反射用时 后第一次回到C点.已知
后第一次回到C点.已知 , 如果光源C沿
, 如果光源C沿 顺时针移动
顺时针移动 后到达
后到达 点,那么光线从
点,那么光线从 出发再经该扇形半径两次反射后第一次回到
出发再经该扇形半径两次反射后第一次回到 所用的时间为( )
所用的时间为( )
 B .
B .  C .
C .  D .
D . 
 ,且向量
,且向量  与
与  平行,则k=( )
平行,则k=( )
 B .
B .  C .
C . 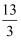 D .
D . 
现需要设计一个仓库,它由上下两部分组成,上部的形状是正四棱锥P﹣A1B1C1D1 , 下部的形状是正四棱柱ABCD﹣A1B1C1D1(如图所示),并要求正四棱柱的高O1O是正四棱锥的高PO1的4倍.

-
(1) 若AB=6m,PO1=2m,则仓库的容积是多少?
-
(2) 若正四棱柱的侧棱长为6m,则当PO1为多少时,仓库的容积最大?
 且
且  ,下列不等式恒成立的是( )
,下列不等式恒成立的是( )
 B .
B .  C .
C .  D .
D . 
 在区间
在区间  上是增函数,则
上是增函数,则  的取值范围是.
的取值范围是.
 >0成立.
>0成立.(1)判断f(x)在[﹣1,1]上的单调性,并证明;
(2)解不等式:f(x+ )<f(
)<f( );
);
(3)若当a∈[﹣1,1]时,f(x)≤m2﹣2am+3对所有的x∈[﹣1,1]恒成立,求实数m的取值范围.
 是定义在
是定义在  上的函数,
上的函数,  是函数
是函数  的导函数,若
的导函数,若  ,
,  ,
,  为自然对数的底数
为自然对数的底数  ,则不等式
,则不等式  的解集是( )
的解集是( )
 B .
B .  C .
C .  D .
D . 

(Ⅰ)求全班人数及中位数,并重新画出频率直方图;
(Ⅱ)若要从分数在  之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在
之间的成绩中任取两个学生成绩分析学生得分情况,在抽取的学生中,求至少有一个分数在  之间的概率.
之间的概率.
 和
和  的前
的前  项和分别为
项和分别为  和
和  ,
,  .若
.若  ,则n的取值集合为( )
,则n的取值集合为( )
 B .
B .  C .
C .  D .
D . 
 满足
满足  (
( 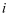 为虚数单位),则
为虚数单位),则  为 ( )
为 ( )
 B .
B .  C .
C .  D .
D . 
 在区间
在区间 上单调递减,则
上单调递减,则 .
.
如图,在△ABC中,已知B=45°,D是BC边上的一点,AD=10,AC=14,DC=6,求AB的长.
 |
指出下列命题中,p是q的什么条件:
(1)p:{x|x>-2或x<3};q:{x|x2-x-6<0};
(2)p:a与b都是奇数;q:a+b是偶数;
(3)p:0<m<![]() ;q:方程mx2-2x+3=0有两个同号且不相等的实根.
;q:方程mx2-2x+3=0有两个同号且不相等的实根.
已知![]()
(1)若![]() ;
;
(2)若函数![]() 在区间
在区间![]() 上是增函数,求实数的取值范围.
上是增函数,求实数的取值范围.
![]()
己知抛物线 C:x 2 =2 py(p>0)的焦点为F,且F与圆M:x 2 + ( y +4 ) 2 =1 上点的距离的最小值为 4 .
( 1 )求 p;
( 2)若点P在M上,P A,PB 是 C的两条切线,A ,B 是切点,求 ![]() PAB 的最大值 .
PAB 的最大值 .
(二)选考题:共 1 0分,请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
- How do you ________ these naughty children? A. do with B
- 填入下列一段文字中横线处的语句,与上下文衔接最恰当的一组是 不是所有的欢笑都表达了高兴,就像______________
- The other day,my friend Jane was invited to a 40th birthday
- Under good treatment, Linda is beginning to _________ and wi
- 正整数按如图的规律排列,请写出第15行,第17列的数字是()A.271 B.270 C.256 D.255
- 把太阳系各行星的轨迹近似的看作匀速圆周运动,则离太阳越远的行星() A. 周期越小
- 下列中央官制形成的先后顺序是 ①三公九卿制 ②三省六部制 ③内阁制 ( )
- 在ABC中,角A、B、C 所对的边分别为 ,cos2C+2cosC+2=0. (Ⅰ)求角C的大小; (Ⅱ)若b
- 阅读下列短文,根据短文内容完成表格中所缺信息,每空一词。Street Markets Around the WorldT
- 图4为近年来影响我国耕地减少的因素构成图。读图,完成下列各题。图中因素对农业用地造成实质性减少的有 A.①② B.②
- 在如图甲所示的电路中,L 1、L 2和L3为三个相同规格的小灯泡,这种小灯泡的伏安特性曲线如图乙所示,当开关S闭合后,电
- 图所示是王濛在2010年温哥华冬奥会500米短道速滑比赛中夺金的场景。在滑行的过程中,冰刀与冰面之间的摩擦为______
- 如图所示,实线是一个电场中的电场线,虚线是一个负检验电荷在这个电场中的轨迹,若电荷是从a处运动到b处,以下判断正确的是
- 明朝永乐帝时设立了内阁制,以内阁作为皇帝处理国政的助理机构。英国“光荣革命”之后,国王威廉三世逐渐以内阁代替枢密院,成为
- 真正的哲学是指( ) A.将一切具体科学包括在内的哲学 B.马克思主义哲学 C.正确反映时代本质要求的哲学
- 如图所示,带箭头的线段表示某一电场的电场线,在电场力作用下(不计重力)一带电粒子经过A点飞向B点,径迹如图中虚线所示,以
- 17.观察下面这幅关于手机的漫画,请以生动形象的语言为其题诗或配文。要求:①符合画面情景;②表达画面内涵;③不超过40字
- 补写出下列各句名篇中的空缺部分(任选3题,多选只按前3题计分共6分) ⑴斜月沉沉藏海雾, ,不知乘月几人归
- 已知点P在第二象限,它的横坐标与纵坐标的和为1,点P的坐标是(写出一个符合条件的一个点即可)
- 下图是四位同学对“化学与健康”这一话题发表的见解,其中正确的是



