高中 数学
已知向量 ,
,  , 且
, 且 , 则实数
, 则实数 .
.
 ,
,  , 且
, 且 , 则实数
, 则实数 .
.
如图,角  以
以  为始边,它的终边与单位圆
为始边,它的终边与单位圆  相交于点
相交于点  ,且点
,且点  的横坐标为
的横坐标为  ,则
,则  的值为( )
的值为( )
 以
以  为始边,它的终边与单位圆
为始边,它的终边与单位圆  相交于点
相交于点  ,且点
,且点  的横坐标为
的横坐标为  ,则
,则  的值为( )
的值为( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数 只有一个零点,则
只有一个零点,则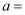 ( )
( )
 只有一个零点,则
只有一个零点,则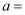 ( )
( )
A . 0
B . 1
C . -1
D . -2
设数列  满足
满足  ,
,  ,若使得
,若使得  ,则正整数
,则正整数  .
.
 满足
满足  ,
,  ,若使得
,若使得  ,则正整数
,则正整数  .
.
已知全集 ,
,  ,
,  , 则a的值为( )
, 则a的值为( )
 ,
,  ,
,  , 则a的值为( )
, 则a的值为( )
A . 2
B . 8
C . 2或8
D . -2或-8
如图,三棱锥 中,
中, 是边长为
是边长为 的正三角形,
的正三角形, ,
,  底面
底面 于点
于点 ,
,  , 且
, 且 .
.
 中,
中, 是边长为
是边长为 的正三角形,
的正三角形, ,
,  底面
底面 于点
于点 ,
,  , 且
, 且 .
.
-
(1) 求证:
 平面
平面 ;
;
-
(2) 求二面角
 的余弦值;
的余弦值;
-
(3) 在棱
 上是否存在点
上是否存在点 , 使得
, 使得 平面
平面 ?若存在,求
?若存在,求 的值;若不存在,说明理由.
的值;若不存在,说明理由.
已知焦点在  轴上的双曲线的渐近线方程为
轴上的双曲线的渐近线方程为  ,则双曲线的离心率为.
,则双曲线的离心率为.
 轴上的双曲线的渐近线方程为
轴上的双曲线的渐近线方程为  ,则双曲线的离心率为.
,则双曲线的离心率为.
在△ABC中,内角A,B,C的对边分别为a,b,c,△ABC的面积 .
.
 .
.
-
(1) 求角A的值;
-
(2) 延长AC至点D,使得CD=AC,且BD=2BC,若c=6,求△ABC的周长.
要测量电视塔AB的高度,在C点测得塔顶的仰角是45°,在D点测得塔顶的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度是( )
A . 30m
B . 40m
C .  m
D .
m
D .  m
m
 m
D .
m
D .  m
m
在平面直角坐标系xoy中直线l的参数方程为  (t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,圆C的极坐标方程为ρ=2.
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,圆C的极坐标方程为ρ=2.
 (t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,圆C的极坐标方程为ρ=2.
(t为参数),以坐标原点O为极点,x轴的正半轴为极轴的极坐标系中,圆C的极坐标方程为ρ=2.
-
(1) 写出直线l的一般方程及圆C的标准方程;
-
(2) 设P(﹣1,1),直线l与圆C相交于A,B两点,求|PA|﹣|PB|的值.
在  中,角
中,角  ,
,  ,
,  所对的边的长分别为
所对的边的长分别为  ,
,  ,
,  ,若
,若  ,则
,则  的形状是( )
的形状是( )
 中,角
中,角  ,
,  ,
,  所对的边的长分别为
所对的边的长分别为  ,
,  ,
,  ,若
,若  ,则
,则  的形状是( )
的形状是( )
A . 锐角三角形
B . 直角三角形
C . 钝角三角形
D . 正三角形
下列“若 , 则
, 则 ”形式的命题中,
”形式的命题中, 是
是 的必要条件的是( )
的必要条件的是( )
 , 则
, 则 ”形式的命题中,
”形式的命题中, 是
是 的必要条件的是( )
的必要条件的是( )
A . 若 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则
, 则
 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 , 则
, 则 D . 若
D . 若 , 则
, 则

用反证法证明某命题时,对结论:“自然数a,b,c中恰有一个是偶数”正确的反设为( )
A. a,b,c中至少有两个偶数 B. a,b,c中至少有两个偶数或都是奇数
C. a,b,c都是奇数 D. a,b,c都是偶数
从0,1,2,3,4,5,6这7个数字中选出4个不同的数字构成四位数,不大于3410的个数是 .
函数![]() 的单调递减区间为 .
的单调递减区间为 .
已知函数f(x)=ex-mx+1的图象为曲线C,若曲线C存在与直线y=ex垂直的切线,则实数m的取值范围是__________.
已知:x,y满足约束条件 ,则
,则![]() 的最小值为 .
的最小值为 .
在等比数列![]() 中,
中,![]() ,
,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(![]() Ⅱ)设
Ⅱ)设![]() ,且
,且![]() 为递增数列,若
为递增数列,若![]() ,求证:
,求证:
![]() .
.
已知点 在抛物线
在抛物线 上,则
上,则 ______;点
______;点 到抛物线
到抛物线 的焦点的距离是______.
的焦点的距离是______.
最近更新
- 已知蜜蜂中的蜂王和工蜂都是二倍体(2n=32),而雄蜂是由未受精的卵细胞直接发育而来。一只雄蜂和一只蜂王交配,F1中工蜂
- 18.Whenever I met him, _____ was fairly often, I like his sw
- (03年天津卷)(18分)两根平行的金属导轨,固定在同一水平面上,磁感强度B=0.50T的匀强磁场与导轨所在平面垂直,导
- 如下图是函数在一个周期内的图像,、分别 是其最高点、最低点,轴,且矩形的面积为. 则的值为 ( )
- 在观看足球世界杯的比赛中,运动员每踢进一个球,都引起全场狂热的欢呼,很多球员出现了心跳加快,面红耳赤、血压升高的现象,这
- 读“1990~2008年湖南省以及全国城市化水平比较图”,完成第11~12题。11.导致湖南省城市化水平如图所示的因素主
- 权力是把双刃剑。有效制约和监督权力的关键是 ( ) A.强化司法机关监督 B.加强政府系统内部监督C.建立健全制约和
- Myuncle will Beijing nextSunday. A. get
- 2011年7月26日上午,我国研制的深海载人潜水器 号成功下潜至5057米水深,标志着我国已进入载人潜水技
- 以下关于波的说法中正确的是[ ](A)干涉现象是波的特征,因此任何两列波相遇时都会产生干涉现象;(B)因为声波的波
- 临床观察发现,人在幼年时期生长激素分泌不足,会引起“侏儒症”;而甲状腺激素分泌不足,则会引起“呆小症”。上述现象说明
- 下列关于直线l,m与平面α,β的命题中,正确的是( ) A.若l⊂β且α⊥β,则l⊥α B.若l⊥β,且α∥β,
- 生物进行一切生命活动的基础,构成细胞结构和生命活动的物质基础,以及生物体生长、发育和繁殖的基础依次为
- 下列关于马丁·路德宗教改革影响的表述,不正确的是 ( ) A.摧毁了德意志的封建势力 B.有力打击了罗
- 下列句中加点成语使用正确的一项是( ) A.惠普网络中国高层换帅尘埃落定,11月15日,新任中国区总经理岑德智首次
- 质点在一平面内沿曲线由P运动到Q。如果用v、a、F分别表示质点运动过程中的速度、加速度和受到的合外力,则下列各图中正确的
- 说:“现在旧的(国际)格局在改变中,但实际并没有结束,新的国际格局还没有形成。”那么20世纪90年代以来的世界政治格局是
- 给定命题:函数和函数的图象关于原点对称;命题:当时,函数取得极小值.下列说法正确的是( )
- 读甲乙两地人口的抽样调查表(表1-4)(每10000人中各年龄段人数及死亡率统计)。下列说法与表格内容相符的是A.甲组人
- 一质量为2kg的物体在如图甲所示的xOy平面上运动,在x方向的v-t图象和y方向的s-t图象分别如图乙、丙所示,下列说法



