高中 数学
已知椭圆  :
:  (
(  )的离心率为
)的离心率为  ,
,  的长轴是圆
的长轴是圆  :
:  的直径.
的直径.
 :
:  (
(  )的离心率为
)的离心率为  ,
,  的长轴是圆
的长轴是圆  :
:  的直径.
的直径.
-
(1) 求椭圆的标准方程;
-
(2) 过椭圆
 的左焦点
的左焦点  作两条相互垂直的直线
作两条相互垂直的直线  ,
,  ,其中
,其中  交椭圆
交椭圆  于
于  ,
,  两点,
两点,  交圆
交圆  于
于  ,
,  两点,求四边形
两点,求四边形  面积的最小值.
面积的最小值.
已知关于x的方程 有实数根.
有实数根.
 有实数根.
有实数根.
-
(1) 求实数a的值;
-
(2) 设
 , 求
, 求 的值.
的值.
已知点A(﹣  ,0),B(
,0),B(  ,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣
,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣  .
.
 ,0),B(
,0),B(  ,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣
,0),P是平面内的一个动点,直线PA与PB交于点P,且它们的斜率之积是﹣  .
.
-
(1) 求动点P的轨迹C的方程;
-
(2) 设直线l:y=kx+1与曲线C交于M、N两点,当线段MN的中点在直线x+2y=0上时,求直线l的方程.
为了了解湖南各景点在大众中的熟知度,随机对15~65岁的人群抽样了  人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
 人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表.
人,回答问题“湖南省有哪几个著名的旅游景点?”统计结果如下图表. | 组号 | 分组 | 回答正确的人数 | 回答正确的人数占本组的频率 |
| 第1组 | [15,25) | | 0.5 |
| 第2组 | [25,35) | 18 | |
| 第3组 | [35,45) | | 0.9 |
| 第4组 | [45,55) | 9 | 0.36 |
| 第5组 | [55,65] | 3 | |

(Ⅰ)分别求出  ,
,  ,
,  ,
,  的值;
的值;
(Ⅱ)从第2,3,4组回答正确的人中用分层抽样的方法抽取6人,求第2,3,4组每组各抽取多少人?
(Ⅲ)在(Ⅱ)抽取的6人中随机抽取2人,求所抽取的人中恰好没有第3组人的概率.
已知  是圆
是圆  内一点,则过点P的最短弦所在直线方程是.
内一点,则过点P的最短弦所在直线方程是.
 是圆
是圆  内一点,则过点P的最短弦所在直线方程是.
内一点,则过点P的最短弦所在直线方程是.
有20位同学,编号从1﹣20,现在从中抽取4人的作问卷进行调查,用系统抽样方法确定所抽的编号为( )
A . 5,10,15,20
B . 2,6,10,14
C . 2,4,6,8
D . 5,8,11,14
已知复数  为纯虚数,则实数
为纯虚数,则实数  ( )
( )
 为纯虚数,则实数
为纯虚数,则实数  ( )
( )
A .  B .
B .  C .
C . 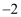 D .
D . 
 B .
B .  C .
C . 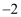 D .
D . 
若不等式ax2+2ax﹣1<0对于一切实数x都恒成立,则实数a的取值范围是( )
A . (﹣∞,﹣1)
B . (﹣1,0)
C .  D .
D . 
 D .
D . 
已知 , 若复数
, 若复数 是纯虚数,则
是纯虚数,则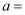 ( )
( )
 , 若复数
, 若复数 是纯虚数,则
是纯虚数,则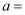 ( )
( )
A . 0
B . 2
C . -1
D . -2
已知集合  ,
,  .
.
 ,
,  .
.
-
(1) 若
 ,
,  ,求实数
,求实数  的取值范围;
的取值范围;
-
(2) 若
 ,且
,且  ,求实数
,求实数  的取值范围.
的取值范围.
在ΔABC中,已知a=1,b=  , A=30°,则B等于;
, A=30°,则B等于;
 , A=30°,则B等于;
, A=30°,则B等于;
在  中,若
中,若  ,则
,则  的形状是( )
的形状是( )
 中,若
中,若  ,则
,则  的形状是( )
的形状是( )
A . 等腰三角形
B . 直角三角形
C . 等腰直角三角形
D . 等腰三角形或直角三角形
已知函数  ,若方程
,若方程  有两个不等实根
有两个不等实根  、
、  ,且
,且  ,则实数
,则实数  的取值范围为
的取值范围为
 ,若方程
,若方程  有两个不等实根
有两个不等实根  、
、  ,且
,且  ,则实数
,则实数  的取值范围为
的取值范围为
已知点  及圆
及圆  :
:  .
.
 及圆
及圆  :
:  .
.-
(1) 若直线
 过点
过点  且与圆心
且与圆心  的距离为1,求直线
的距离为1,求直线  的方程;
的方程;
-
(2) 设过点P的直线
 与圆
与圆  交于
交于  、
、  两点,当
两点,当  时,求以线段
时,求以线段  为直径的圆
为直径的圆  的方程;
的方程;
已知集合 ,
,  , 则
, 则 的必要不充分条件可能是( )
的必要不充分条件可能是( )
 ,
,  , 则
, 则 的必要不充分条件可能是( )
的必要不充分条件可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
要得到y![]() =3×(
=3×(![]() )x的图象,只需将函数y=(
)x的图象,只需将函数y=(![]() )x的图象( )
)x的图象( )
A.向左平移3个单位 B.向右平移3个单位
C.向左平移1个单位 D.向右平移1个单位
若集合![]()
![]() 则
则![]() ( )
( )
![]()
![]()
![]()
![]()
![]()
![]() . 2
. 2 ![]() .
.![]()
若实数x,y满足不等式组
 且z=x+3y的最大值为12,则实数k=( )
且z=x+3y的最大值为12,则实数k=( )
A.﹣12 B.![]()
![]() C.﹣9 D.
C.﹣9 D.![]()
![]()
设集合A={1,2,3},集合B={2,3,4},则A∩B=( )
A.{1} B.{1,4} C.{2,3} D.{1,2,3,4}
若实数x,y满足等式(x-2)2+y2=3,那么![]() 的最大值为( )
的最大值为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 一个有穷等比数列的首项为,项数为偶数,如果其奇数项的和为,偶数项的和为,求此数列的公比和项数。
- A newly-published study has shown that loneliness can spread
- 截至2007年9月,全国登记注册的个体私营企业从业人员共计1.1亿多人。2007年,私营企业税收总额为4771.5亿元,
- 在干冰晶体中每个CO2分子周围紧邻的 CO2分子有___________个 在晶体中截取一个最小的正方形;使正方形的四
- 已知抛物线与x轴有两个交点,则m的取值范围是
- 第二卷(非选择题,共两大题,35分) 第四部分: 任务型阅读 (共10小题;每小题l分, 满分l0分) 请认真阅读下列短
- 1.76g铜镁合金完全溶解于50mL密度为1.40g/mL、质量分数为63%的浓硝酸中,得到NO2气体1792mL(标准
- 在一定条件下,将1mol CO和1 mol水蒸气混合后发生如下变化:CO(g)+H2O(g)CO2(g)+H2(g)若反
- 已知等比数列{an},S6=10,q=-,则a1+a6等于( )A.17 B.14
- 最近美国的《农业研究》杂志报道,半胱氨酸[HS—CH2—CH(NH2)—COOH]能增强艾滋病感染者的免疫力,对控制艾滋
- 工业上利用CO和水蒸气在一定条件下发生反应制取氢气: CO(g)+H2O(g) CO2(g)+H2(g) △H=-41
- 无法不对你残酷 ①弟弟考上北京的大学时,与我当年一样大,17岁。母亲要我回去接他上学,我想起这么多年一个人走过的路,便坚
- 下列生活行为不符合“绿色、节能、低碳”的是( ) A、垃圾分类回收,废物再利用 B、出门尽量步行或骑自行车 C、使
- 常温下,向25mL0.1mol∙L-1NaOH溶液中逐滴加入0.1mol∙L-1 CH3COOH溶液,曲线如图所示,有关
- 下图是单克隆抗体制备流程的简明示意图。下列有关叙述,正确的是 A.①是从已免疫的小鼠脾脏中获得的效应T淋巴细胞 B.②
- . 将函数的图象向左平移个单位后,得到函数的图象,则等于( ) A. B. C
- 下图中的虚线为南半球中纬地区低压的槽线,完成如果槽线西北端的气压低于东南端,则槽线东北和西南的风向分别为A.和
- ----Shall I give you a ride as you live so far away?----Tha
- 已知函数对任意的实数,满足,且当时,,则( ) A、 B、 C、 D
- Why do youturn to me for help_____ you can easily wor



