高中 数学
 是
是  的导函数, 且
的导函数, 且  .
. (I)求a的值;
(II)求函数  在区间
在区间  上的最值.
上的最值.
 =(sinθ,
=(sinθ, ),
), =(1,cosθ),其中θ∈(﹣
=(1,cosθ),其中θ∈(﹣ ,
,  ),则|
),则| +
+ |的范围是
|的范围是
 -1
C .
-1
C .  D . 2
D . 2 
 中,若
中,若 是方程
是方程 的两根,则
的两根,则 的值是( )
的值是( )
 C .
C .  D .
D . 
 轴上的椭圆
轴上的椭圆  过点
过点  ,且离心率为
,且离心率为  ,
,  为
为  的右焦点,
的右焦点,  为
为  上一点,
上一点,  轴,圆
轴,圆  的半径为
的半径为  .
.
-
(1) 求椭圆
 和圆
和圆  的方程;
的方程;
-
(2) 若直线
 与圆
与圆  交于
交于  两点,与椭圆
两点,与椭圆  交于
交于  两点,其中
两点,其中  在第一象限,是否存在
在第一象限,是否存在  使
使  ?若存在,求
?若存在,求  的方程;若不存在,说明理由.
的方程;若不存在,说明理由.
 , 则
, 则 .
.
 B . 事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下,第二次恰好取得黄球”的概率都等于
B . 事件“直到第二次才取到黄色球”与事件“第一次取到白球的情况下,第二次恰好取得黄球”的概率都等于 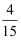 C . 事件“直到第二次才取到黄色球”的概率等于
C . 事件“直到第二次才取到黄色球”的概率等于  ,事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率等于
,事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率等于 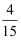 D . 事件“直到第二次才取到黄色球”的概率等于
D . 事件“直到第二次才取到黄色球”的概率等于 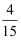 ,事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率等于
,事件“第一次取得白球的情况下,第二次恰好取得黄球”的概率等于 
 中,已知底面四边形
中,已知底面四边形  为正方形,且
为正方形,且  ,其中,设
,其中,设  ,
,  ,体对角线
,体对角线  ,则
,则  的值是.
的值是. 
 ,
,  ,则
,则  ( )
( )
 B .
B .  C . 5
D .
C . 5
D . 
 ,则
,则  的虚部为( )
的虚部为( )
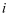 D . -i
D . -i
 ,其导函数
,其导函数  ,且函数
,且函数  在
在  处有极值
处有极值 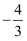 .
.
-
(1) 求实数
 的值;
的值;
-
(2) 求函数
 在
在  上的最大值和最小值.
上的最大值和最小值.
-
(1) 求f(log2
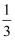 )的值;
)的值;
-
(2) 求f(x)的解析式.
 的前
的前  项和为
项和为  ,
,  ,
,  ,则
,则  的值为.
的值为.
 中,角
中,角  的对边分别为
的对边分别为  ,当
,当  的外接圆半径
的外接圆半径  时,
时,  面积的最大值为( )
面积的最大值为( )
 B .
B .  C .
C .  D .
D . 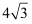
级别 | 54公斤级 | 59公斤级 | 64公斤级 | 70公斤级 | 76公斤级 |
体重 |
|
|
|
|
|
级别 | 83公斤级 | 91公斤级 | 99公斤级 | 108公斤级 | 108公斤级以上 |
体重 |
|
|
|
|
|
每个级别的比赛分为抓举与挺举两个部分,最后综合两部分的成绩得出总成绩,所举重量最大者获胜,在该次举重比赛中,获得金牌的运动员的体重以及举重成绩如下表
体重 | 54 | 59 | 64 | 70 | 76 | 83 | 91 | 99 | 106 |
举重成绩 | 291 | 304 | 337 | 353 | 363 | 389 | 406 | 421 | 430 |
参考数据: ;
;
参考公式: .
.
-
(1) 根据表中的数据,求出运动员举重成绩
 与运动员的体重
与运动员的体重 的回归直线方程(保留1位小数);
的回归直线方程(保留1位小数);
-
(2) 某金牌运动员抓举成绩为180公斤,挺举成绩为218公斤,则该运动员最有可能是参加的哪个级别的举重?
-
(3) 凯旋回国后,中央一台记者从团队的10人中随机抽取3人进行访谈,用
 表示抽取到的是金牌得主的人数,求
表示抽取到的是金牌得主的人数,求 的概率分布列与数学期望.
的概率分布列与数学期望.
在数列 




总有


A . 



(2![]() )0+2-2·(2
)0+2-2·(2![]() )
)![]() +(
+(![]() )0.5+
)0.5+![]() ;
;
.若方程![]() 表示圆,则实数m的取值范围是( ).
表示圆,则实数m的取值范围是( ).
![]()
![]()
![]()
![]()
已知函数![]()
(1)当![]() 时,求
时,求![]() 的值域.
的值域.
(2)若存在区间![]() ,使
,使![]() 在
在![]() 上值域为
上值域为![]() ,求
,求![]() 的取值范围.
的取值范围.
- 已知数列满足,若,则_____.
- 生活处处有化学.下列变化属于化学变化的是() A.葡萄酿成酒 B.水果榨成果汁 C.蔗糖溶于水
- In 2015, a bill allowing every couple to have two children w
- 规范的操作是实验成功的前提,实验操作正确的是()A. 蒸发操作时,蒸发皿必须放在石棉网上,用酒精灯外焰加热 B. 取少量
- 如图是三个对数函数的图象,则a、b、c的大小关系是() A.a>b>c B.c>b>a C.c>a>b
- 下列各组的两种物质在溶液中的反应,可用同一离子方程式表示的是() A.氢氧化钠与盐酸;氢氧化钠与碳酸 B.BaCl2溶液
- 关于分子的热运动,下列说法正确的是( )A.分子的热运动就是布朗运动B.布朗运动是液体分子的无规则运动C.温度越高
- 阅读下面一首唐诗,然后回答问题。 江汉 杜甫 江汉思归客,乾坤一腐儒。 片云天共远,水夜月同孤。 落日心犹壮,秋风病欲苏
- (10分)如图所示,三棱镜的顶角是30º,出射光线与入射光线夹角也为30º。问:(1)该三棱镜的折射率是多大?(2)光在
- 现代科学研究表明,多种微生物参与了腐乳的发酵,其中起主要作用的是() A.青霉
- 机动灵活,周转速度快,装卸方便,对各种自然条件适应性强的运输方式是 ( ) A.航空 B.公路 C.铁路
- 人的糖蛋白必须经内质网和高尔基体进一步加工合成,通过转基因技术,可以使人的糖蛋白基因得以表达的受体细胞是 A、大肠杆菌
- 在氮源为14N和15N的培养基上生长的大肠杆菌,其DNA分子分别为14N-DNA(相对分子质量为a)和15N-DNA(相
- 为了迎接将于2014年10月在荆州古城举行的湖北省第十四届运动会,荆州市的园林工人们在新建的荆州市体育运动中心的广场上移
- 从编号为1~50的50枚最新研制的某种型号的导弹中随机抽取5枚来进行发射实验,若采用每部分选取的号码间隔一样的系统抽样方
- 身高1.7 m的人在平面镜前1.5 m处,平面镜高1 m,则人在平面镜中的像高 m。人和像的距离是 m。当
- 通常用来衡量一个国家的石油化学工业发展水平的标志是 ( ) A.石油的年产
- 用均匀导线做成的正方形线圈边长为l,正方形的一半放在垂直于纸面向里的匀强磁场中,如图所示,当磁场以的变化率增强时,则A.
- 现有失去标签的氯化钙、硝酸银、盐酸、碳酸钠四种无色溶液,为了鉴别四种溶液各是什么,将它们随意编号为A、B、C、D后,按下
- 下列各组植物中,生活环境中和繁殖方式最相似的是 A.墙藓、肾蕨 B.水绵、水稻 C.海带、雪松 D













