高中 数学
对于函数f(x)=asinx+bx+c(其中,a,b∈R,c∈Z),选取a,b,c的一组值计算f(1)和f(﹣1),所得出的正确结果一定不可能是( )
A . 4和6
B . 3和1
C . 2和4
D . 1和2
设集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知三棱锥P﹣ABC的所有棱长都相等,现沿PA,PB,PC三条侧棱剪开,将其表面展开成一个平面图形,若这个平面图形外接圆的半径为  ,则三棱锥P﹣ABC的体积为
,则三棱锥P﹣ABC的体积为
 ,则三棱锥P﹣ABC的体积为
,则三棱锥P﹣ABC的体积为
方程  的解集为.
的解集为.
 的解集为.
的解集为.
已知函数f(x)=  x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
 x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
x2+2ax,g(x)=3a2lnx+b,设两曲线y=f(x),y=g(x)有公共点,且在该点处的切线相同,则a∈(0,+∞)时,实数b的最大值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
i是虚数单位,则复数  在复平面内对应的点在象限.
在复平面内对应的点在象限.
 在复平面内对应的点在象限.
在复平面内对应的点在象限.
设函数  .
.
 .
.
-
(1) 求不等式
 的解集;
的解集;
-
(2) 若关于
 的不等式
的不等式  在
在  上无解,求实数
上无解,求实数  的取值范围.
的取值范围.
抛物线  和直线
和直线  所围成的封闭图形的面积是( )
所围成的封闭图形的面积是( )
 和直线
和直线  所围成的封闭图形的面积是( )
所围成的封闭图形的面积是( )
A .  B .
B .  C .
C . 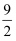 D .
D . 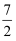
 B .
B .  C .
C . 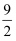 D .
D . 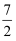
设点O是面积为6的△ABC内部一点,且有  +
+  +2
+2  =
=  ,则△AOC的面积为
,则△AOC的面积为
 +
+  +2
+2  =
=  ,则△AOC的面积为
,则△AOC的面积为
若物体的运动规律是s=f(t),则物体在时刻t0的瞬时速度可以表示为( )
⑴  ;⑵
;⑵  ;
;
⑶  ;⑷
;⑷  .
.
A . (1)(2)
B . (1)(3)
C . (2)(3)
D . (2)(4)
已知公差不为零的等差数列{an}中,a3=7,又a2 , a4 , a9成等比数列.
-
(1) 求数列{an}的通项公式;
-
(2) 设bn=
 ,求数列{bn}的前n项和Sn .
,求数列{bn}的前n项和Sn .
函数f(x)=2sin(ωx+φ)(ω>0,﹣ <φ<
<φ< )的部分图象如图所示,则f(0)=( )
)的部分图象如图所示,则f(0)=( )
 <φ<
<φ< )的部分图象如图所示,则f(0)=( )
)的部分图象如图所示,则f(0)=( )
A . - B . -
B . - C . -1
D . -
C . -1
D . -
 B . -
B . - C . -1
D . -
C . -1
D . -
如果一双曲线的实轴及虚轴分别是另一双曲线的虚轴及实轴,则称此两双曲线互为共轭双曲线.已知双曲线 ,
,  互为共轭双曲线,
互为共轭双曲线, 的焦点分别为
的焦点分别为 ,
,  , 顶点分别为
, 顶点分别为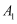 ,
,  ,
,  的焦点分别为
的焦点分别为 ,
,  , 顶点分别为
, 顶点分别为 ,
,  , 过四个焦点的圆的面积为
, 过四个焦点的圆的面积为 , 四边形
, 四边形 的面积为
的面积为 , 则
, 则 的最大值为( )
的最大值为( )
 ,
,  互为共轭双曲线,
互为共轭双曲线, 的焦点分别为
的焦点分别为 ,
,  , 顶点分别为
, 顶点分别为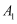 ,
,  ,
,  的焦点分别为
的焦点分别为 ,
,  , 顶点分别为
, 顶点分别为 ,
,  , 过四个焦点的圆的面积为
, 过四个焦点的圆的面积为 , 四边形
, 四边形 的面积为
的面积为 , 则
, 则 的最大值为( )
的最大值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  .
.
 .
.
-
(1) 若
 恒成立,求a的取值范围;
恒成立,求a的取值范围;
-
(2) 在(1)的条件下,
 有两个不同的零点
有两个不同的零点  ,求证:
,求证:  .
.
(12分)某中学的高二(1)班男同学有![]() 名,女同学有
名,女同学有![]() 名,老师按照分层抽样的方法组建了一个
名,老师按照分层抽样的方法组建了一个![]() 人的课外兴趣小组.
人的课外兴趣小组.
(Ⅰ)求某同学被抽到的概率及课外兴趣小组中男、女同学的人数;
(Ⅱ)经过一个月的学习、讨论,这个兴趣小组决定选出两名同学做某项实验,方法是先从小组里选出![]() 名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
名同学做实验,该同学做完后,再从小组内剩下的同学中选一名同学做实验,求选出的两名同学中恰有一名女同学的概率;
(Ⅲ)试验结束后,第一次做试验的同学得到的试验数据为![]() ,第二次做试验的同学得到的试验数据为
,第二次做试验的同学得到的试验数据为![]() ,请问哪位同学的实验更稳定?并说明理由.
,请问哪位同学的实验更稳定?并说明理由.
过点![]() 且与直线l:
且与直线l:![]() 平行的直线方程为_________.
平行的直线方程为_________.
定义在R上的函数f(x)满足f(x)+f′(x)<e,f(0)=e+2(其中e为自然对数的底数),则不等式exf(x)>ex+1+2的解集为( )
A.(﹣∞,0) B.(﹣∞,e+2) C.(﹣∞,0)∪(e+2,+∞) D.(0,+∞)
下列命题是真命题的是
(A)![]() 的充要条件 (B)
的充要条件 (B)![]() 的充分条件
的充分条件
(C)![]() (D)若
(D)若![]() 为真命题,则
为真命题,则![]() 为真
为真
已知函数f(x)=![]()
![]() +x在x=1处的切线方程为2x﹣y+b=0.
+x在x=1处的切线方程为2x﹣y+b=0.
(Ⅰ)求实数a,b的值;
(Ⅱ)设函数g(x)=f(x)+![]()
![]() x2﹣kx,且g(x)在其定义域上存在单调递减区间(即g′(x)<0在其定义域上有解),求实数k的取值范围.
x2﹣kx,且g(x)在其定义域上存在单调递减区间(即g′(x)<0在其定义域上有解),求实数k的取值范围.
已知双曲线 的渐近线方程为
的渐近线方程为 ,则
,则 ( )
( )
A. B.
B.  C.
C.  D. 12
D. 12
A.
最近更新
- 下列物质的分离(或提纯)方法正确的是A.分离乙醇与乙酸——萃取 B.提纯硝酸钾(含少量氯化钾)——蒸发结晶
- Do you often________books on Sundays? A.lookat B.see
- ________ is often the casewith old people, my grandfather i
- 若复数是纯虚数(是虚数单位),则的值为 A. B. C. D.
- 将纯锌片和纯铜片按图示方式插入同浓度同体积的稀硫酸中一段时间,以下叙述正确的是A.两烧杯中铜片表面均无气泡产生B.甲中铜
- 至2006年,科学家确认,地球上的海水中蕴藏了大约40万亿吨氘。从1升海水里提取的氘,在聚变反应中所释放的能量,相当于燃
- 下列现象不能用质量守恒定律解释的是 A.煤燃烧后变成煤灰,煤灰的质量比煤的质量小B.蜡烛燃烧后逐渐变短 C.镁条燃
- 做下列物质在氧气中燃烧的实验之前,为防止集气瓶炸裂,先要在集气瓶底放水 或铺沙的是…………………………………………………
- 公元前452~公元前450年间,罗马共和国先后铸造十二块铜牌,详细列出民法、刑法、诉讼程序等许多方面的内容,公布于罗马广
- 通过对金属和金属材料的学习,你认为下列做法正确的是 A.将硫酸铜溶液盛放在铁桶里 B.要制取2 g氢气,用56 g生铁与
- 下列各组中属于同位素关系的是A.与 B.T2O与H2O C.与 D.金刚石与石墨
- 阅读材料回答问题: 材料一:材料二:有学者指出:“康熙帝过于追求个人兴趣,传教士在宫廷进讲的内容完全是以皇帝的兴趣为转移
- 下列变化中有一种与其它三种不同的是() A.钢铁生锈 B.食物腐败 C.分离液态空气制氧气 D.用氮气制化肥
- A、B是治疗同一种疾病的两种药,用若干试验组进行对比试验。每个试验组由4只小白鼠组成,其中2只服用A,另2只服用B,然后
- They forced ____ little children to work all day for so litt
- —Andyisn’t going out this evening, is she? —_______.She has
- (坐标系与参数方程选做题)在极坐标系中,过点引圆的一条切线,则切线长为 .
- 近年来时有农民工因讨债不成,而选择在公共场合跳楼,以吸引公众和社会关注,意图使问题得以解决。对此,你认为 ①这种
- 依次填入下面一段文字横线处的语句,衔接最恰当的一组是(3分)( ) 内心里拥有善, , ,
- 近年来科学家报导大气圈的臭氧层严重受损,造成紫外线增强的现象。紫外线为高能量的光线,在生物体内易激发超氧化物的形成,致使



