高中 数学
如果直线(3a+2)x+ay-1=0与直线2ax+y-2a+1=0互相平行,则实数a的值为 ( )
A . 0或-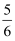 B . -
B . - C . 2
D . 2或-
C . 2
D . 2或-
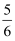 B . -
B . - C . 2
D . 2或-
C . 2
D . 2或-
若三点A(3,1),B(-2,b),C(8,11)在同一直线上,则实数b等于( )
A . 2
B . 3
C . 9
D . -9
已知  ,
,  ,
,  ,则
,则  ,
,  ,
,  的大小关系为( )
的大小关系为( )
 ,
,  ,
,  ,则
,则  ,
,  ,
,  的大小关系为( )
的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在数列{an}中,a1=3,  ,则通项公式an = .
,则通项公式an = .
 ,则通项公式an = .
,则通项公式an = .
已知函数  ,
,  .
.
 ,
,  .
.
-
(1) 若函数
 存在两个极值,求
存在两个极值,求  的取值范围;并证明:函数
的取值范围;并证明:函数  存在唯一零点.
存在唯一零点.
-
(2) 若存在实数
 ,
,  ,使
,使  ,且
,且  ,求
,求  的取值范围.
的取值范围.
化简 .
.
 .
.
已知集合  ,
,  ,则
,则  ( ).
( ).
 ,
,  ,则
,则  ( ).
( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
等边  的边长为1,点
的边长为1,点  在其外接圆劣弧
在其外接圆劣弧  上,则
上,则  的最大值为.
的最大值为.
 的边长为1,点
的边长为1,点  在其外接圆劣弧
在其外接圆劣弧  上,则
上,则  的最大值为.
的最大值为.
已知数列  是等差数列,数列
是等差数列,数列  是各项均为正数的等比数列,且
是各项均为正数的等比数列,且  ,
,  ,
,  .
.
 是等差数列,数列
是等差数列,数列  是各项均为正数的等比数列,且
是各项均为正数的等比数列,且  ,
,  ,
,  .
.
-
(1) 求数列
 和
和  的通项公式;
的通项公式;
-
(2) 设
 ,求数列
,求数列  的前
的前  项和.
项和.
已知四棱锥  中,底面
中,底面  为菱形,
为菱形,  ,平面
,平面  平面
平面  ,
,  ,点E,F分别为
,点E,F分别为 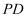 ,
,  上的一点,且
上的一点,且  ,
,  .
.
 中,底面
中,底面  为菱形,
为菱形,  ,平面
,平面  平面
平面  ,
,  ,点E,F分别为
,点E,F分别为 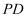 ,
,  上的一点,且
上的一点,且  ,
,  .
. 
-
(1) 求证:

 平面
平面  ;
;
-
(2) 求
 与平面
与平面  所成角的正弦值.
所成角的正弦值.
已知双曲线C:  =1(a>0,b>0)的两条渐近线均与圆(x﹣2)2+y2=1相切,则双曲线的离心率为.
=1(a>0,b>0)的两条渐近线均与圆(x﹣2)2+y2=1相切,则双曲线的离心率为.
 =1(a>0,b>0)的两条渐近线均与圆(x﹣2)2+y2=1相切,则双曲线的离心率为.
=1(a>0,b>0)的两条渐近线均与圆(x﹣2)2+y2=1相切,则双曲线的离心率为.
设等差数列  前
前  项和为
项和为  ,等差数列
,等差数列  前
前  项和为
项和为  ,若
,若  ,则
,则  ( )
( )
 前
前  项和为
项和为  ,等差数列
,等差数列  前
前  项和为
项和为  ,若
,若  ,则
,则  ( )
( )
A . 528
B . 529
C . 530
D . 531
复数  (
( 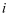 为虚数单位)的共轭复数在复平面内对应的点在第三象限,则实数
为虚数单位)的共轭复数在复平面内对应的点在第三象限,则实数  的取值范围是( )
的取值范围是( )
 (
( 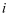 为虚数单位)的共轭复数在复平面内对应的点在第三象限,则实数
为虚数单位)的共轭复数在复平面内对应的点在第三象限,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若m>n,则( )
A . 0.2m<0.2n
B . log0.3m>log0.3n
C . 2m<2n
D . m2>n2
已知函数  .
.
 .
.
-
(1) 当
 时,解方程
时,解方程  .
.
-
(2) 当
 时,
时,  恒成立,求实数
恒成立,求实数  的取值范围.
的取值范围.
如图为平面中两个全等的直角三角形,将这两个三角形绕着它们的对称轴(虚线所在直线)旋转一周得到一个几何体,则该几何体的体积为.

将曲线 
变换得到曲线方程为


A . 



已知数列![]() 的前
的前![]() 项和
项和![]() .
.
求数列![]() 的通项公式;
的通项公式;
证明:对任意![]() ,都有
,都有![]() ,使得
,使得![]() 成等比数列.
成等比数列.
函数y=sinx+cosx+2的最小值是( )
A.2-![]() B.2+
B.2+![]()
C.0 D.1
已知![]() ,
,![]() 为虚数单位,若
为虚数单位,若![]() ,则
,则![]() __________.
__________.
最近更新
- 用落体运动验证机械能守恒定律的实验.(1)为进行该实验,备有下列器材可供选择:A铁架台、B(电磁)打点计时器、C复写纸片
- 马说韩愈( 11分 )世有伯乐,然后有千里马。千里马常有,而伯乐不常有。故虽有名马,祇辱于奴隶人之手,骈死于槽枥之间,不
- 已知抛物线的准线过双曲线的一个焦点, 且双曲线的离心率为2, 则该双曲线的方程为 .
- 下列分子中的σ键是由一个原子的s轨道和另一个原子的p轨道以“头碰头”方式重叠构建而成的是A.H2
- 国画,又称“中国画”,国画在内容和艺术创作上,反映了中华民族的民族意识和审美情趣,体现了古人对自然、社会及与之相关联的政
- 诗歌《一个民族的荣光》中写到:“一次又一次,我们一起受挫,一起流泪,一起欢笑。因为一种力量、一种精神,总能让我们找到前进
- 用NA代表阿伏加德罗常数的值,下列说法正确的是 A.1.0L 1.0mol
- 下列化学反应不属于置换反应的是 A.H2+ CuOCu + H2O
- 下列化合物中阴离子半径和阳离子半径之比最大的是() A. LiI B.NaBr
- 现有质量分数为98%的浓硫酸100g,将上述浓硫酸稀释成质量分数为20%的稀硫酸.需要加入水的质量是多少() A.290
- “工商业的发展导致了资产阶级——由平民出身、从事贸易或其他资本主义冒险事业的人组成的中产阶级——的相应发展。到l9世纪末
- (08广东三校期末联考)某人生病的时候,医生开给他抗生素,医生总是告诉他一直服用抗生素,直到服完为止,其原因是 A
- I.请指出下列过程需要破坏的作用力 ①离子键 ②极性共价键③非极性共价键④氢键⑤分子间作用力 (1)干冰熔化
- .右图展示了现代国际关系中一次重要的大国 较量。下列关于此事件叙述不正确的是 A.发生在两极格局正式确立后 B.全面冷战
- 已知向量,若,则x= .
- 历史上,安培曾经提出分子环形电流的假说来解释为什么磁体具有磁性,他认为在物质微粒的内部存在着一种环形的分子电流,分子电流
- (1)键线式 表示的分子式___________;名称是___________。 (2)中含有的官能团的名称为_____
- Lucy: Does Aunt Tara enjoy? Mark: Yes. She has three dogs,
- 某共价化合物含C、H、N 3种元素,分子内有4个N原子,且4个N原子排列成空间的四面体(如白磷分子结构),每两个N原子间
- 32.仿照例句抄写下面句子(要求:书写工整、清晰、美观、大方)。 例句:我慢慢地、慢慢地了解到,所谓父女母子一场,只不过



