高中 数学
江岸边有一炮台高30米,江中有两条船,由炮台顶部测得两条船俯角分别为45°和30°,而且两条船与炮台底部连线成30°角,则两条船相距 ( )
A . 150米
B . 120米
C . 100米
D . 30米
已知集合  ,
,  ,则
,则  =( )
=( )
 ,
,  ,则
,则  =( )
=( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知一扇形的半径为2,面积为4,则此扇形圆心角的绝对值为弧度.
已知A、B、C三个箱子中各装有2个完全相同的球,每个箱子里的球,有一个球标着号码1,另一个球标着号码2.现从A、B、C三个箱子中各摸出1个球.
(I)若用数组(x,y,z)中的x、y、z分别表示从A、B、C三个箱子中摸出的球的号码,请写出数组(x,y,z)的所有情形,并回答一共有多少种;
(Ⅱ)如果请您猜测摸出的这三个球的号码之和,猜中有奖.那么猜什么数获奖的可能性最大?请说明理由.
抛物线  的焦点到直线
的焦点到直线  的距离为
的距离为  ,则
,则 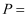 ( )
( )
 的焦点到直线
的焦点到直线  的距离为
的距离为  ,则
,则 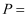 ( )
( )
A . 1
B . 2
C .  D . 4
D . 4
 D . 4
D . 4
若α∈(0,π),且3cos2α=sin(  ﹣α),则sin2α的值为( )
﹣α),则sin2α的值为( )
 ﹣α),则sin2α的值为( )
﹣α),则sin2α的值为( )
A . 1或﹣  B .
B .  C . 1
D . -
C . 1
D . - 
 B .
B .  C . 1
D . -
C . 1
D . - 
已知实数 ,
,  ,
,  , 且满足
, 且满足 , 则下列判断正确的是( )
, 则下列判断正确的是( )
 ,
,  ,
,  , 且满足
, 且满足 , 则下列判断正确的是( )
, 则下列判断正确的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数 
 的部分图象如图所示,为了得到
的部分图象如图所示,为了得到  的图象,可以将
的图象,可以将  的图象( )
的图象( )

 的部分图象如图所示,为了得到
的部分图象如图所示,为了得到  的图象,可以将
的图象,可以将  的图象( )
的图象( )
A . 向右平移  个单位长度
B . 向左平移
个单位长度
B . 向左平移  个单位长度
C . 向右平移
个单位长度
C . 向右平移  个单位长度
D . 向左平移
个单位长度
D . 向左平移  个单位长度
个单位长度
 个单位长度
B . 向左平移
个单位长度
B . 向左平移  个单位长度
C . 向右平移
个单位长度
C . 向右平移  个单位长度
D . 向左平移
个单位长度
D . 向左平移  个单位长度
个单位长度
设集合M={x|x|x2﹣2x﹣3<0,x∈Z},则集合M的真子集个数为( )
A . 8
B . 7
C . 4
D . 3
若全集A={x|x≥2015},且集合B={x|2015<x≤2050,x∈N},则下列选项中正确的是( )
A . A与B都是有限集
B . A是有限集,B是无限集
C . A⊆B
D . A∩B是有限集
“ ”是“函数
”是“函数 有且只有一个零点”的( )
有且只有一个零点”的( )
 ”是“函数
”是“函数 有且只有一个零点”的( )
有且只有一个零点”的( )
A . 必要不充分条件
B . 充分不必要条件
C . 充要条件
D . 既不充分也不必要条件
对任意的两个实数a,b,定义  ,若f(x)=4﹣x2 , g(x)=3x,则min(f(x),g(x))的最大值为.
,若f(x)=4﹣x2 , g(x)=3x,则min(f(x),g(x))的最大值为.
 ,若f(x)=4﹣x2 , g(x)=3x,则min(f(x),g(x))的最大值为.
,若f(x)=4﹣x2 , g(x)=3x,则min(f(x),g(x))的最大值为.
数列{ }定义如下:
}定义如下: =1,当
=1,当 时,
时, , 若
, 若 , 则n的值等于( )
, 则n的值等于( )
A . 7
B . 8
C . 9
D . 10
函数 在
在 处的切线方程为(写成一般式方程的形式).
处的切线方程为(写成一般式方程的形式).
 在
在 处的切线方程为(写成一般式方程的形式).
处的切线方程为(写成一般式方程的形式).
已知数列![]() 满足
满足![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)证明:![]() .
.
已知甲、乙两组数据如茎叶图所示,若它们的中位数相同,平均数也相同,则图中的![]()

A. 7 B. 8 C. 9 D. 10
设平面内有n条直线(n≥3),其中有且仅有两条直线互相平行,任意三条直线不过同一点,若用f(n)表示这n条直线的交点的个数,则f(4)=______;当n>4时,f(n)=____________________(用n表示).
设f(x)是定义在R上单调递减的奇函数,若x1+x2>0,x2+x3>0,x3+x1>0,则( )
A.f(x1)+f(x2)+f(x3)<0
B.f(x1)+f(x2)+f(x3)>0
C.f(x1)+f(x2)+f(x3)=0
D.f(x1)+f(x2)>f(x3)
一袋中共有个大小相同的黑球![]() 个和白球
个和白球![]() 个.
个.
(1) 若从袋中任意摸![]() 出
出![]() 个球,求至少有
个球,求至少有![]() 个白球的概率..
个白球的概率..
(2)现从中不放回地取球,每次取![]() 个球,取
个球,取![]() 次,已知第
次,已知第![]() 次取得白球,求第
次取得白球,求第![]() 次取得黑球的概率.
次取得黑球的概率.
最近更新
- 如表是黄豆和玉米种子食用部分营养成分表(表中数据表示每百克含量),从表中分析可得出哪项结论
- 密码子存在于 A.DNA B.mRNA C.tRNA D.核糖体
- 将1 mol X、3 mol Y充入一个密闭容器中,在一定条件下发生如下反应并达到平衡:X(g)+3Y(g)2Z(g);
- (1) 当时,求函数的定义域; (2) 若函数的定义域为,求的取值范围。
- 明清是我国封建社会的衰落时期,也是专制君主制度的顶峰时期,其专制主义加强的表现包括 ①明朝废除丞相,设立内阁
- 下面词语书写错误最多的一项是() A.惩罚 操炼 斑澜 恭恭敬敬 丛山叠岭 惊涛澎湃 B.宛转 怪诞 泛
- 有关日本经济的说法,错误的是( ) A.经济十分发达,是世界上的经济强国 B.工业原料和燃料主要从国外进口 C.工
- 已知函数为 (1)求函数的定义域; (2)求函数的单调区间。
- 以下说法正确的是 ( ) A.原子是化学变化中的最小微粒,即化学变化不产生新元素。核反应产生了新元素不属于化
- Five passengers were _____ in the traffic accident and they
- 过原点的直线与椭圆=1(a>b>0)相交于A、B两点,若F(-c,0)是椭圆的左焦点,则△FAB的最大面积是( )
- 绿色植物在白天可进行() A.光合作用 B.呼吸作用 C.蒸腾作用 D.以上三种都有
- 之所以说相对论的提出是物理学思想的一次重大革命,主要是因为相对论( )①否定了经典力学的绝对时空论 ②深刻地揭示了
- 下列各句中,没有语病的一句是( )(2分) A.马航MH370班机失联后,机上239人的安危牵动每个人的心
- 下列变化过程属于物理变化的是 A.用谷物、葡萄酿制美酒 B.以石油为原料制造药物 C.分离
- 下列关于我国地形特点的叙述,正确的是( ) A.山区面积广,发展种植业优势大 B.山区面积广,有利于发展农业多种经
- NA代表阿伏加德罗常数值,下列说法正确的是…( )A.78 g Na2O2所含有的离子数为3NAB.1 mol甲基
- 晏殊《浣溪沙》中的“________________________,________________________。
- VI.短文改错(共10小题;每小题1分,满分10分) 此题要求改正所给短文中的错误。对标有题号的每一行作出判断:如无错误
- 下图示意某区域某月一条海平面等压线,图中N地气压高于P地.读下图,完成N地风向为A. 东北风



