高中 数学
现行普通高中学生在高一升高二时面临着选文理科的问题,学校抽取了部分男、女学生意愿的一份样本,制作出如下两个等高堆积条形图:

根据这两幅图中的信息,下列统计结论是不正确的是( )
A . 样本中的女生数量多于男生数量
B . 样本中有理科意愿的学生数量多于有文科意愿的学生数量
C . 样本中的男生偏爱理科
D . 样本中的女生偏爱文科
若函数  ,当
,当 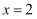 时,函数
时,函数  有极值为
有极值为 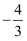 ,
,
 ,当
,当 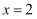 时,函数
时,函数  有极值为
有极值为 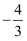 ,
,
-
(1) 求函数
 的解析式;
的解析式;
-
(2) 若
 有
有  个解,求实数
个解,求实数  的取值范围.
的取值范围.
已知  ,若数列
,若数列  的前
的前  项和
项和  ,则
,则 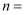
 ,若数列
,若数列  的前
的前  项和
项和  ,则
,则 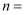
如图,四棱锥  中,
中,  平面
平面  ,
,  ,
,  ,
,  ,
,  为
为  的中点.
的中点.
 中,
中,  平面
平面  ,
,  ,
,  ,
,  ,
,  为
为  的中点.
的中点. 
(Ⅰ)证明:平面  平面
平面  ;
;
(Ⅱ)求异面直线 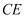 与
与 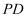 所成角的余弦值;
所成角的余弦值;
(Ⅲ)求直线  与平面
与平面  所成角的正弦值.
所成角的正弦值.
把长为12厘米的细铁丝截成两段,各自围成一个正三角形,那么这两个三角形的面积之和的最小值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
在我国古代数学名著《九章算术》中,把两底面为直角三角形的直棱柱称为“堑堵”.已知三棱柱  是一个“堑堵”,其中
是一个“堑堵”,其中  ,点
,点  是
是  的中点,则四棱锥
的中点,则四棱锥  的外接球的表面积为.
的外接球的表面积为.
 是一个“堑堵”,其中
是一个“堑堵”,其中  ,点
,点  是
是  的中点,则四棱锥
的中点,则四棱锥  的外接球的表面积为.
的外接球的表面积为.
在四边形ABCD中, , 且·
, 且· , 则四边形ABCD是( )
, 则四边形ABCD是( )
 , 且·
, 且· , 则四边形ABCD是( )
, 则四边形ABCD是( )
A . 矩形
B . 菱形
C . 直角梯形
D . 等腰梯形
设数列  的前n 项和为
的前n 项和为  ,满足
,满足  ,
,  ,且
,且  成等差数列
成等差数列
 的前n 项和为
的前n 项和为  ,满足
,满足  ,
,  ,且
,且  成等差数列
成等差数列
-
(1) 求
 的值
的值
-
(2) 求数列
 的通项公式
的通项公式
 内角
内角  ,
,  ,
,  的对边分别为
的对边分别为  ,
,  ,
,  ,且
,且  .
.

-
(1) 求角A;
-
(2) 若
 ,延长
,延长 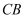 至
至  .使
.使  ,且
,且  ,点
,点  在
在  上,且
上,且  ,求
,求  的面积.
的面积.
已知函数f(x)=  ,g(x)=lnx,则函数y=f(x)﹣g(x)的零点个数为( )
,g(x)=lnx,则函数y=f(x)﹣g(x)的零点个数为( )
 ,g(x)=lnx,则函数y=f(x)﹣g(x)的零点个数为( )
,g(x)=lnx,则函数y=f(x)﹣g(x)的零点个数为( )
A . 1
B . 2
C . 3
D . 4
如图,在棱长为2的正方体ABCD—A1B1C1D1中,O是底面ABCD的中心,E、F分别是CC1、AD的中点.那么异面直线OE和FD1所成角的余弦值为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知等差数列  和
和  的前
的前  项和分别为
项和分别为  和
和  ,且满足
,且满足  ,则
,则  ( )
( )
 和
和  的前
的前  项和分别为
项和分别为  和
和  ,且满足
,且满足  ,则
,则  ( )
( )
A .  B .
B .  C .
C . 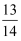 D . 1
D . 1
 B .
B .  C .
C . 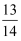 D . 1
D . 1
已知数列  的通项公式为
的通项公式为  ,这个数列中的项摆放成如图所示的数阵.记
,这个数列中的项摆放成如图所示的数阵.记  为数阵从左至右的
为数阵从左至右的  列,从上到下的
列,从上到下的  行共
行共  个数的和,则数列
个数的和,则数列  的前2020项和为.
的前2020项和为.
 的通项公式为
的通项公式为  ,这个数列中的项摆放成如图所示的数阵.记
,这个数列中的项摆放成如图所示的数阵.记  为数阵从左至右的
为数阵从左至右的  列,从上到下的
列,从上到下的  行共
行共  个数的和,则数列
个数的和,则数列  的前2020项和为.
的前2020项和为. 
定义在  上的偶函数
上的偶函数  在
在  上是减函数,则( )
上是减函数,则( )
 上的偶函数
上的偶函数  在
在  上是减函数,则( )
上是减函数,则( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
平面  的法向量是
的法向量是  ,点
,点  在平面
在平面  内,则点
内,则点  到平面
到平面  的距离为.
的距离为.
 的法向量是
的法向量是  ,点
,点  在平面
在平面  内,则点
内,则点  到平面
到平面  的距离为.
的距离为.
若关于 的方程
的方程 有两个不同的实根,则
有两个不同的实根,则 的取值可以是( )
的取值可以是( )
 的方程
的方程 有两个不同的实根,则
有两个不同的实根,则 的取值可以是( )
的取值可以是( )
A . 2
B .  C .
C .  D . 3
D . 3
 C .
C .  D . 3
D . 3
设![]() ,若
,若![]() 是
是![]() 的充分不必要条件,则实数
的充分不必要条件,则实数![]() 的取值范围是__ _.
的取值范围是__ _.
解下列不等式:
![]()
在各项均为正数的等比数列![]() 中,若
中,若![]() ,则
,则![]() ……
……![]() 等于( )
等于( )
A. 5 B. 6 C. 7 D. 8
.已知函数 若
若![]() ,
,![]() ,则
,则![]() ___________.
___________.
最近更新
- ÷=________.
- — May I remind you that a Mr Li is waiting outside, sir???—
- (1)《中华人民共和国国歌》的词作者是 ,曲作者是聂耳。 (2)吾尝终日而思矣,
- Ifyou want to take an adventure travel lasting a day or two,
- 下列措施不能够防止发酵液被污染的是( ) A.榨汁机要清洗干净,并晾干 B.发酵瓶要清洗干净,用体积分数为70%的
- 阅读下面短文,从每题所给的四个选项中,选出最佳答案。 Hi, dear boys and girls! Do you k
- 1.下列加点字的注音没有错误的一组是( )(3分)A.迤逦(yǐ) 稽手(qǐ) 芙蓉浦(pǔ)
- 下图模拟的是呼吸时膈肌的运动情况,请根据图回答下列问题:(每空2分,本题共12分)(1)图中气球代表的是肺,瓶底的橡皮膜
- 已知a1=1,an+1-an=2n-n. (1)求a2,a3; (2)求证:an=
- 用氧化物X测定空气受CO的污染的程度,发生化学反应的方程式为:X+5CO=I2+5CO2 根据CO2的多少,可测定CO的
- 要得到函数的图象,只需将函数的图象 A.右移个单位 B.右移个单位 C.左移个单位 D
- 下列加点字注音有误的一项是( )A.长袍(páo)菜肴(yáo)几碟(dié)扉(fēi)页B.停滞(zì) 扼(è)
- 北宋兴起的景德镇后来发展成为著名的瓷都。( )
- 象征意象就是代表某一实体事物或某种精神内容的意象。出现在诗歌中的只是象征体,而被象征的本体则隐去了,这样就使得诗歌更耐人
- (23分)“创新是一个民族的灵魂。”中国作为一个历史悠久的多民族国家,在政治制度创新方面多有建树,而且其体系之完备,经验
- 自来水消毒过程中常会发生如下化学反应,其反应的微观过程可用下图表示: (1)图乙所示反应的基本反应类型为
- 下列装置或操作能达到实验目的的是
- (7分)请分析下面两个生态系统中的食物网简图,回答问题: (1)食物网A描述了具有多种生物的生态系统,其获取食物的路径具
- _____the test paper, the student put down his pen, _____ wi
- (15分,每小题各3分)下图中,A到L为常见物质或该物质的水溶液,B在A气体 中燃烧产生棕黄色烟,B、G为中学化学中常见



