高中 数学
若角600°的终边上有一点(-4,a),则a的值是( )
A . 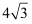 B .
B .  C .
C .  D .
D . 
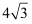 B .
B .  C .
C .  D .
D . 
已知向量 ,
,  , 则下列说法正确的是( )
, 则下列说法正确的是( )
 ,
,  , 则下列说法正确的是( )
, 则下列说法正确的是( )
A . 若
 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 与
与 的夹角为120°,则
的夹角为120°,则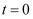 或
或 D . 若
D . 若 与
与 的夹角为锐角,则
的夹角为锐角,则

 , 则
, 则 B . 若
B . 若 , 则
, 则 C . 若
C . 若 与
与 的夹角为120°,则
的夹角为120°,则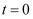 或
或 D . 若
D . 若 与
与 的夹角为锐角,则
的夹角为锐角,则
投掷两枚质地均匀的正方体散子,将两枚散子向上点数之和记作  .在一次投掷中,已知
.在一次投掷中,已知  是奇数,则
是奇数,则  的概率是( )
的概率是( )
 .在一次投掷中,已知
.在一次投掷中,已知  是奇数,则
是奇数,则  的概率是( )
的概率是( )
A .  B .
B . 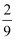 C .
C .  D .
D . 
 B .
B . 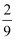 C .
C .  D .
D . 
已知  ,
,  为
为  的反函数,不等式
的反函数,不等式  的解集为
的解集为 
 ,
,  为
为  的反函数,不等式
的反函数,不等式  的解集为
的解集为 
(I)求集合 
(II)当  时,求函数
时,求函数  的值域.
的值域.
已知向量  =(k,1),
=(k,1),  =(1,0),
=(1,0),  =(﹣2,k).若
=(﹣2,k).若  +
+  ⊥
⊥  ,则k=.
,则k=.
 =(k,1),
=(k,1),  =(1,0),
=(1,0),  =(﹣2,k).若
=(﹣2,k).若  +
+  ⊥
⊥  ,则k=.
,则k=.
-
(1) 已知
 ,且
,且  为第三象限角,求
为第三象限角,求  的值
的值
-
(2) 已知
 ,计算
,计算  的值.
的值.
已知函数  ,a∈R.
,a∈R.
 ,a∈R.
,a∈R.
-
(1) 若使函数f(x)在[a,+∞)上为减函数,求a的取值范围;
-
(2) 若关于x的方程f(x)=﹣1+log0.5(x+3)在[1,3]上仅有一解,求实数a的取值范围.
已知函数  ,且满足
,且满足  ,对任意的实数
,对任意的实数  都有
都有  成立.
成立.
 ,且满足
,且满足  ,对任意的实数
,对任意的实数  都有
都有  成立.
成立.
-
(1) 求
 的解析式;
的解析式;
-
(2) 若
 在
在  上是单调递减函数,求实数
上是单调递减函数,求实数  的取值范围.
的取值范围.
从m(  且
且  )个男生、6个女生中任选2个人当发言人,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则
)个男生、6个女生中任选2个人当发言人,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则  .
.
 且
且  )个男生、6个女生中任选2个人当发言人,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则
)个男生、6个女生中任选2个人当发言人,假设事件A表示选出的2个人性别相同,事件B表示选出的2个人性别不同.如果A的概率和B的概率相等,则  .
.
已知直角梯形ABCD中,  是边长为2的等边三角形,AB=5.沿CE将
是边长为2的等边三角形,AB=5.沿CE将  折起,使B至
折起,使B至 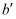 处,且
处,且  ;然后再将
;然后再将 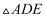 沿DE折起,使A至
沿DE折起,使A至 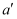 处,且面
处,且面  面CDE,
面CDE,  和
和  在面CDE的同侧.
在面CDE的同侧.
 是边长为2的等边三角形,AB=5.沿CE将
是边长为2的等边三角形,AB=5.沿CE将  折起,使B至
折起,使B至 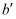 处,且
处,且  ;然后再将
;然后再将 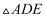 沿DE折起,使A至
沿DE折起,使A至 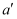 处,且面
处,且面  面CDE,
面CDE,  和
和  在面CDE的同侧.
在面CDE的同侧.
(Ⅰ) 求证:  平面CDE;
平面CDE;
(Ⅱ) 求平面  与平面CDE所构成的锐二面角的余弦值.
与平面CDE所构成的锐二面角的余弦值.
已知y=f(x)是定义在R上的奇函数,当x>0时,f(x)=x﹣2,那么不等式  的解集是( )
的解集是( )
 的解集是( )
的解集是( )
A .  B .
B .  C .
C .  或
或  D .
D .  或
或 
 B .
B .  C .
C .  或
或  D .
D .  或
或 
将函数 的图象向左平移
的图象向左平移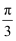 个单位长度,得到的图象对应的函数解析式为( )
个单位长度,得到的图象对应的函数解析式为( )
 的图象向左平移
的图象向左平移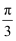 个单位长度,得到的图象对应的函数解析式为( )
个单位长度,得到的图象对应的函数解析式为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
sin20°cos40°+cos20°sin40°的值等于( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
棱长为2的正四面体的四个顶点都在同一个球面上,若过该球球心的一个截面如图所示,求图中三角形(正四面体的截面)的面积.

平面上两定点  ,动点
,动点  满
满  (
(  为常数).
为常数).
 ,动点
,动点  满
满  (
(  为常数).
为常数). (Ⅰ)说明动点  的轨迹(不需要求出轨迹方程);
的轨迹(不需要求出轨迹方程);
(Ⅱ)当  时,动点
时,动点  的轨迹为曲线
的轨迹为曲线  ,过
,过  的直线
的直线  与
与  交于
交于  两点,已知点
两点,已知点  ,证明:
,证明:  .
.
已知双曲线  -
-  =1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
 -
-  =1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
=1(a>0,b>0)的左顶点与抛物线y2=2px(p>0)的焦点的距离为4,且双曲线的一条渐近线与抛物线的准线的交点坐标为(-2,-1),则双曲线的焦距为( )
A . 2  B . 2
B . 2  C . 4
C . 4  D . 4
D . 4 
 B . 2
B . 2  C . 4
C . 4  D . 4
D . 4 
已知F是椭圆E:![]() 的左焦点,P是椭圆E上的动点,A(1,
的左焦点,P是椭圆E上的动点,A(1,![]() )为一个定点,则|PA|+|PF|的最大值为 。
)为一个定点,则|PA|+|PF|的最大值为 。
不论![]() 为何值,函数
为何值,函数![]() 的图象一定经过点P,则点P的坐标为___________.
的图象一定经过点P,则点P的坐标为___________.
在如图所示的正方形中随机投掷10000个点,若曲线![]() 的方程为
的方程为![]() ,则落入阴影部分的点的个数的估计为( )
,则落入阴影部分的点的个数的估计为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()

在 中,角
中,角 的对边分别为
的对边分别为 ,若
,若 ,
, 则
则 ____.
____.
最近更新
- 图甲为广东省佛山市产业分布示意图,图乙为佛山市顺德区家具生产专业镇联系示意图。读图,完成下列各题。 (1).佛山市工、农
- 补写出下列名句名篇的空缺部分。(两个小题任选一个小题。) (1)______,一弦一柱思华年。______, _____
- 《史记·周本纪》载:“(武王)十一年将伐纣,卜龟兆,不吉,风雨暴至。群公尽惧,唯太公强之,劝武王,武王于是遂行(伐纣决战
- 如图所示,向烧杯内倾倒二氧化碳气体时所观察到的现象是 , 该实验说明二氧化碳具
- 3a.(-2a)²=( ) A. B. C.
- 、从社会转型的角度看,英国《权利法案》的颁布表明 ( ) A.国王已经
- 我国人民崇敬屈原并每年纪念他,主要是因为他( )A.在文学上成就巨大 B.
- 某学生离家去学校,由于怕迟到,所以一开始就匀速跑步,等跑累了再匀速走余下的路程. 在下图中纵轴表示离学校的距离d,横轴表
- 下列说法正确的是()A. 高钙奶可为人体补充钙元素 B. MgO中Mg元素是+1价 C. 天然气的主要成分是CO D.
- 图1为世界某区域甲地的一个居住小区图片,图2为该区域等温线示意图,回答1-3题。1.据图判断a、b、c、d四条等温线数值
- 19世纪中叶,生活在英格兰彻斯特的桦尺蛾大多数是浅灰色的,但一百年以后,曼彻斯特变成了一个工业城市,而此时生活在此地的桦
- 未来三年,我国将投入8450亿元用于缓解群众“看病难、看病贵”的问题.将8450亿 用科学记数法表示为( ).
- 已知,t是大于0的常数,且函数的最小值为9,则t的值为( )A.4 B.6
- 2003年10月5日,我国自行研制的“神舟”五号载人飞船发射成功,假定宇航员杨利伟在舱内做以下实验,关于实验结果以下说法
- 已知点P在以F1,F2为焦点的椭圆+=1(a>b>0)上,若•=0,tan∠PF1F2=,则该椭圆的离心率为() A.
- 下列各组中的俗称和化学名称均表示同一种物质的是A.生石灰—氢氧化钙 B.酒精—乙醇
- 下列说法中正确的是()A. 两个直角三角形全等 B. 两个等腰三角形全等 C. 两个等边三角形全等 D. 两条直角边对应
- 鞍钢和宝钢区位选择不同,说明了: A.原料地对工业区位的影响正在加强 B.动力对工业区位的影响在加强 C.劳动力对工业
- 如果一个种群的密度愈来愈小,下列选项中与之无关的是( ) A.种群处于衰退期 B.种群内雄性趋于不育 C.种群死亡
- 补全对话从每题A\ B\ C.D四个选项中,选出一个最佳答案完成对话。(5分) -Lee,____ 66 Teac



