高中 数学
如图,点A,B,C,M,N为正方体的顶点或所在棱的中点,则下列各图中,满足直线  平面ABC的是( )
平面ABC的是( )
 平面ABC的是( )
平面ABC的是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知幂函数  的图象过点
的图象过点  ,则其解析式为
,则其解析式为  .
.
 的图象过点
的图象过点  ,则其解析式为
,则其解析式为  .
.
将函数  的图象向右平移
的图象向右平移  个单位长度后,得到的函数的图象关于点
个单位长度后,得到的函数的图象关于点  对称,则函数
对称,则函数  在
在  上的最小值是( )
上的最小值是( )
 的图象向右平移
的图象向右平移  个单位长度后,得到的函数的图象关于点
个单位长度后,得到的函数的图象关于点  对称,则函数
对称,则函数  在
在  上的最小值是( )
上的最小值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数y=f(x)的大致图象如图所示,则函数y=f(x)的解析式应为( )

A . f(x)=x﹣  B . f(x)=x+
B . f(x)=x+  C . f(x)=
C . f(x)=  D . f(x)=x+
D . f(x)=x+ 
 B . f(x)=x+
B . f(x)=x+  C . f(x)=
C . f(x)=  D . f(x)=x+
D . f(x)=x+ 
关于  的方程
的方程  的解为
的解为 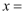 .
.
 的方程
的方程  的解为
的解为 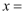 .
.
若复数  的实部与虚部之和为零,则b的值为( )
的实部与虚部之和为零,则b的值为( )
 的实部与虚部之和为零,则b的值为( )
的实部与虚部之和为零,则b的值为( )
A . 2
B .  C .
C .  D .
D . 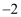
 C .
C .  D .
D . 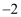
直线  的倾斜角是( )
的倾斜角是( )
 的倾斜角是( )
的倾斜角是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设向量  ,
,  满足|
满足|  +
+  |=
|=  ,|
,|  ﹣
﹣  |=
|=  ,则
,则  •
•  =( )
=( )
 ,
,  满足|
满足|  +
+  |=
|=  ,|
,|  ﹣
﹣  |=
|=  ,则
,则  •
•  =( )
=( )
A . 1
B . 2
C . 3
D . 5
如图,已知  是
是  内角
内角  的角平分线.
的角平分线.
 是
是  内角
内角  的角平分线.
的角平分线. 
-
(1) 用正弦定理证明:
 ;
;
-
(2) 若
 ,
,  ,
,  ,求
,求  的长.
的长.
已知△ABC的三个顶点是  ,
,  ,
,  .
.
 ,
,  ,
,  .
.
-
(1) 求
 边的高所在直线
边的高所在直线  的方程;
的方程;
-
(2) 若直线
 过
过  点,且
点,且  ,
,  到直线
到直线  的距离相等,求直线
的距离相等,求直线  的方程.
的方程.
设a>1,b>0,若a+b=2,则 的最小值为
的最小值为
 的最小值为
的最小值为
A .  B . 6
C .
B . 6
C .  D .
D . 
 B . 6
C .
B . 6
C .  D .
D . 
过点(0,1)作直线,使它与抛物线y2=4x仅有一个公共点,这样的直线有( )
A . 1条
B . 2条
C . 3条
D . 4条
下面几何体的截面一定是圆面的是( )
A . 圆台
B . 球
C . 圆柱
D . 棱柱
函数  的单调递增区间是( )
的单调递增区间是( )
 的单调递增区间是( )
的单调递增区间是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知集合 , 若
, 若 , 则实数
, 则实数 .
.
 , 若
, 若 , 则实数
, 则实数 .
.
已知等差列![]() 的前n项和为
的前n项和为![]()
(1)求数列 ![]() 的通项公式:
的通项公式:
(2)若函数![]() 在
在![]() 处取得最大值,且最大值为a2,求函数
处取得最大值,且最大值为a2,求函数![]() 的解析式。
的解析式。
已知等比数列{an}的前n项和为Sn,且公比q>1,a1=1![]() ,S4=5S2.
,S4=5S2.
(1)求an;
(2)设bn=2nan,求数列{bn}的前n项和Tn.
下列函数中,以π为周期的偶函数是( )
(A)y=|sin x| (B)y=sin |x| (C)y=sin(2x+![]() ) (D)y=sin(x+
) (D)y=sin(x+![]() )
)
为了分析某个高三学生的学习状态,对其下一阶段的学习提供指导性建议.现对他前![]() 次考试的数学成绩
次考试的数学成绩![]() 、物理成绩
、物理成绩![]() 进行分析.下面是该生
进行分析.下面是该生![]() 次考试的成绩.
次考试的成绩.
| 数学 | 108 | 103 |
| 112 | 128 | 120 | 132 |
| 物理 | 74 | 71 | 88 | 76 | 84 | 81 | 86 |
(Ⅰ)他的数学成绩与物理成绩哪个更稳定?请给出你的说明;
(Ⅱ)已知该生的物理成绩![]() 与数学成绩
与数学成绩![]() 是线性相关的,求物理成绩
是线性相关的,求物理成绩![]() 与数学成绩
与数学成绩![]() 的回归直线方程
的回归直线方程
(Ⅲ)若该生的物理成绩达到90分,请你估计他的数学成绩大约是多少?
(附: )
)
1876年4月1日,加菲尔德在《新英格兰教育日志》上发表了勾股定理的一种证明方法,即在如图的直角梯形 中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”,可以简洁明了地推证出勾股定理.1881年加菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、易懂的证明,就把这一证明方法称为“总统证法”.如图,设
中,利用“两个全等的直角三角形和一个等腰直角三角形的面积之和等于直角梯形面积”,可以简洁明了地推证出勾股定理.1881年加菲尔德就任美国第二十任总统.后来,人们为了纪念他对勾股定理直观、易懂的证明,就把这一证明方法称为“总统证法”.如图,设 ,在梯形
,在梯形 中随机取一点,则此点取自等腰直角
中随机取一点,则此点取自等腰直角 中(阴影部分)的概率是()
中(阴影部分)的概率是()

A. B.
B.  C.
C.  D.
D. 

A.
最近更新
- 艾滋病(AIDS)是由人类免疫缺陷病毒(HIV)引起的。感染了HIV的人称为艾滋病病毒感染者,当病毒将人体免疫力破坏到一
- The work is not worth doing ________ cash, but I am getting
- 恩格斯指出:“任何哲学只不过是在思想上反映出来的时代内容”这说明 A. 哲学属于思想文化范畴 B. 任何哲学都是一定社会
- (2014·上海浦东新区高考预测)下图是2013年2月17日中午卫星拍摄的美国南加州海岸上空形成的大气涡流。该涡流呈逆
- ____ economy, Shanghai isalready the biggest city in China.
- 公司经营成功的主要因素有哪些? 公司要制定 ;公司要提高 能力,依靠 、科学管
- 某碳酸钙和氧化钙组成的混合物中钙元素的质量分数为50%,将8.0g该混合物高温煅烧至固体质量不再改变,则生成二氧化碳的质
- 如图所示,一小球A与一个白炽灯泡S紧靠在一起,小球在灯泡的右侧,小球可看做质点,灯泡可视为一点光源,P为一个竖直放置的屏
- 某历史兴趣小组的同学准备去实地探访古代“丝绸之路”,他们不应该去的省份是 A.四川 B.陕西
- Buying tickets from the Fringe Box Office… Counter:
- 关于我国家庭电路和安全用电,下列说法错误的是 A.家庭电路的电压是220VB.家庭电路中的用电器都是并联的C.只有36V
- 我国是一个多民族的国家,历史上各民族共同创造了中华文明。 渤海政权仿照唐朝实行郡县制,农业采用中原先进技术。这种状况最能
- 经国务院批准,中国银行、中国建设银行、中国工商银行改制为股份制银行。一些国有商业银行改制为股份制银行,主要是改变了 A.
- 落红不是无情物,__________________。(龚自珍《己亥杂诗》)
- 据《史记·平津侯主父列传》载:“元元黎民,得免于战国,逢明天子,人人自以为更生。”此段文字表明秦朝统一的意义是A.使人民
- 小理家准备买新房,他看到某开发商的广告称“乘车从新楼盘到一家大型商场的时间只需3分钟”。据此你认为从新楼盘到该大型商场比
- 近亲结婚后代患遗传病的可能性增大的原因是,血缘关系越近( ) A.生活环境越相同 B.染色体数目越相同 C.生活
- 下列离子方程式书写正确的是
- 在图所示的电路中,电源电压保持不变.闭合电键S,小灯发光较暗.一段时间后,小灯明显变亮,且电压表与电流表示数比值不变,据
- (本题满分12分)中内角的对边分别为, 向量且 (Ⅰ)求锐角的大小, (Ⅱ)如果,求的面积的最大值



