高中 数学
某学校为了调查学生在学科教辅书方面的支出情况,抽出了一个容量为  的样本,其频率分布直方图如图所示,其中支出的钱数在
的样本,其频率分布直方图如图所示,其中支出的钱数在  的同学比支出的钱数在
的同学比支出的钱数在  的同学多26人,则
的同学多26人,则  的值为.
的值为.
 的样本,其频率分布直方图如图所示,其中支出的钱数在
的样本,其频率分布直方图如图所示,其中支出的钱数在  的同学比支出的钱数在
的同学比支出的钱数在  的同学多26人,则
的同学多26人,则  的值为.
的值为.
 是虚数单位,则复数
是虚数单位,则复数  在复平面上对应的点位于( )
在复平面上对应的点位于( )
A . 第一象限
B . 第二象限
C . 第三象限
D . 第四象限
在正方体 中,下列结论正确的有( )
中,下列结论正确的有( )
 中,下列结论正确的有( )
中,下列结论正确的有( )
A .  是平面A1B1C1D1的一个法向量
B .
是平面A1B1C1D1的一个法向量
B .  是平面
是平面 的一个法向量
C .
的一个法向量
C .  D .
D . 
 是平面A1B1C1D1的一个法向量
B .
是平面A1B1C1D1的一个法向量
B .  是平面
是平面 的一个法向量
C .
的一个法向量
C .  D .
D . 
复数  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A . 1
B .  C .
C . 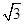 D . 2
D . 2
如图,三棱锥 中,平面
中,平面 平面
平面 ,
,  , 点
, 点 分别是棱
分别是棱 的中点,点
的中点,点 是
是 的重心.
的重心.
 中,平面
中,平面 平面
平面 ,
,  , 点
, 点 分别是棱
分别是棱 的中点,点
的中点,点 是
是 的重心.
的重心.
-
(1) 证明:

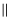 平面
平面 ;
;
-
(2) 若
 为正三角形,求平面
为正三角形,求平面 与平面
与平面 夹角的余弦值.
夹角的余弦值.
已知集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设随机变量ξ~N(2,1),若P(ξ>3)=m,则p(1<ξ<3)等于( )
A .  ﹣2m
B . 1﹣m
C . 1﹣2m
D .
﹣2m
B . 1﹣m
C . 1﹣2m
D .  ﹣m
﹣m
 ﹣2m
B . 1﹣m
C . 1﹣2m
D .
﹣2m
B . 1﹣m
C . 1﹣2m
D .  ﹣m
﹣m
如图,根据算法的程序框图,当输入n=6时,输出的结果是( )

A . 35
B . 84
C . 49
D . 25
在两个变量y与x的回归模型中,分别选择了4个不同模型,它们的 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
 如下,其中拟合效果最好的模型是( )
如下,其中拟合效果最好的模型是( )
A . 模型1的 为0.975
B . 模型2的
为0.975
B . 模型2的 为0.79
C . 模型3的
为0.79
C . 模型3的 为0.55
D . 模型4的
为0.55
D . 模型4的 为0.25
为0.25
 为0.975
B . 模型2的
为0.975
B . 模型2的 为0.79
C . 模型3的
为0.79
C . 模型3的 为0.55
D . 模型4的
为0.55
D . 模型4的 为0.25
为0.25
某厂的产值若每年平均比上一年增长10%,经过x年后,可以增长到原来的2倍,在求x时,所列的方程正确的是( )
A . (1+10%)x-1=2
B . (1+10%)x='2'
C . (1+10%)x+1=2
D . x=(1+10%)2
已知函数  ,若
,若  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
 ,若
,若  ,则实数
,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C . 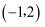 D .
D . 
 B .
B .  C .
C . 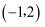 D .
D . 
已知正四棱锥 的底面是边长为
的底面是边长为 的正方形,其体积为
的正方形,其体积为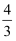 , 若圆柱的一个底面的圆周经过正方形的四个顶点,另一个底面的圆心为该棱锥的高的中点,则该圆柱的表面积为( )
, 若圆柱的一个底面的圆周经过正方形的四个顶点,另一个底面的圆心为该棱锥的高的中点,则该圆柱的表面积为( )
 的底面是边长为
的底面是边长为 的正方形,其体积为
的正方形,其体积为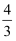 , 若圆柱的一个底面的圆周经过正方形的四个顶点,另一个底面的圆心为该棱锥的高的中点,则该圆柱的表面积为( )
, 若圆柱的一个底面的圆周经过正方形的四个顶点,另一个底面的圆心为该棱锥的高的中点,则该圆柱的表面积为( )
A . π
B . 2π
C . 4π
D . 6π
在区间[-1,4]上任意取一个数x , 则x∈[0,1]的概率是( )
A .  B .
B . 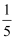 C .
C .  D .
D . 
 B .
B . 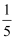 C .
C .  D .
D . 
已知函数![]() 。
。
(1)若![]() 为方程
为方程![]() 的两个实根,并且A,B为锐角,求m的取值范围;
的两个实根,并且A,B为锐角,求m的取值范围;
(2)对任意实数![]() ,恒有
,恒有![]() ,证明:
,证明:![]() .
.
已知抛物线![]() 的焦
的焦![]() 点为F,点
点为F,点![]() 为直线
为直线![]() 与抛物线
与抛物线![]() 准线的交点,直线
准线的交点,直线![]() 与抛物线
与抛物线![]() 相交于
相交于![]() 、
、![]() 两点,点A关于
两点,点A关于![]() 轴的对称点为D .
轴的对称点为D .
(1)求抛物线![]() 的方程。
的方程。
(2)证明:点![]() 在直线
在直线![]() 上;
上;
(3)设![]() ,求
,求![]() 的面积。.
的面积。.
函数y=|2x-1|的大致图象是( )

已知函数![]() ,其中
,其中![]() 为自然对数的底数.
为自然对数的底数.
(1)试判断函数![]() 的单调性;
的单调性;
(2)若对任意的![]() ,不等式
,不等式![]() 恒成立,求实数
恒成立,求实数![]() 的取值范围.
的取值范围.
在《爸爸去哪儿》第二季第四期中,村长给6位“萌娃”布置一项搜寻空投食物的任务。已知:①食物投掷地点有远、近两处;②由于Grace年纪尚小,所以要么不参与该项任务,但此时另需一位小孩在大本营陪同,要么参与搜寻近处投掷点的食物;③所有参与搜寻任务的小孩须被均分成两组,一组去远处,一组去近处,那么不同的搜寻方案有
A.80 种 B.70 种 C.40 种 D.10种
已知函数![]() (其中
(其中![]() 为参数).
为参数).
(1)求函数![]() 的单调区间;
的单调区间;
(2)若对任意![]() ,都有
,都有![]() 成立,求实数
成立,求实数![]() 的取值集合;
的取值集合;
(3)证明:![]() (其中
(其中![]() ,
,![]() 为自然对数的底数)
为自然对数的底数)
某几何体的三视图如图所示,则该几何体的表面积为

最近更新
- I haven’t read ____ of his books, but judging from the one I
- The traffic rule says young children under the age of four a
- 苹果汁是人们喜爱的饮料。由于此饮料中含有Fe2+,现榨的苹果汁在空气中会由淡绿色变为棕黄色(Fe3+)。若榨汁时加入维生
- 下图为“1月份60°N附近的气温、气压分布曲线图”,根据所提供的信息完成下列问题。(1)图中的两条曲线分别是:A____
- 乌尔比安的《论告示》中记载:“如果洗衣人收到了一件交付清洗的衣服,而老鼠将衣服咬坏了。那么,洗衣人要对此依照承揽之诉承担
- 阅读短文,回答问题 “磨”到最后 王晓河 ①“我磨墨,墨磨我”,这是画家韩羽的一枚书法印章。他自幼热爱文学、戏剧。搞漫画
- —Where is Bill? —He ________ Sydney with his father.
- 博鳌亚洲论坛2008年年会4月12日下午在海南博鳌开幕。巴基斯坦总统穆沙拉夫、蒙古国总统恩赫巴亚尔、斯里兰卡总统拉贾帕克
- 《后汉书.许荆传》所记,荆之祖八武被举孝廉,欲令两弟成名,便“共割财产,以为三分,自取肥田广宅奴婢强者”。这样,他的两个
- 濠州定远县①一弓手②,善用矛,远近皆服其能。有一偷亦善击刺,常蔑视官军,唯与此弓手不相下,曰:“见必与之决生死。”一日,
- 已知数列的前n项和…,那么数列( ) A.是等差数列但不是等比数列 B.是等比数列但不是等差数列
- 下列各项搭配完全正确的一项是 A.《陋室铭》——《周元公集》——周敦颐——北宋 B.《桥梁远景图》——说明文——茅以升—
- 一个四面体的顶点在空间直角坐标系Oxyz中的坐标分别是(1,0,1),(1,1,0),(0,1,1),(0,0,0),画
- 自来水消毒过程中通常会发生如下化学反应,其反应的微观过程可用下图表示:表示氯原子, 表示氧原子, 表示氢原子,D的化学
- 人们从事商业活动,都要在一定的地点进行,我国的许多城市就是在商业发展的基础上兴起的。结合下图回答下面下列各题。①②③④四
- 若数列满足,则称为数列,记. (Ⅰ)写出一个E数列A5满足; (Ⅱ)若,n=2000,证明:
- 关于摩擦力做功,下列叙述正确的是() A.摩擦力做功的多少只与初位置和末位置有关,与运动路径无关 B.滑动摩擦力总是做负
- 细胞内糖分解代谢过程如下图,下列叙述错误的是A.植物细胞能进行过程①和③或过程①或④ B.真核细胞的细胞质基质中能进行过
- 目前,中央在城市中清理各种歧视农民工的法律和法规,维护进城农民工的合法权益。这主要体现了 A.个人利益与国家利益
- 下列词语中划线字读音完全相同的一项是【 】(2分)A.峡谷瑕疵 遐迩目不暇接B.哄笑洪水 拱门共商大计C.镶嵌道歉赚



