高中 数学
如图,四棱锥P﹣ABCD的底面ABCD为菱形,PB=PD,E,F分别为AB和PD的中点.

-
(1) 求证:EF∥平面PBC;
-
(2) 求证:平面PBD⊥平面PAC.
已知实数λ>0,设函数f(x)=eλx﹣  .
.
 .
.(Ⅰ)当λ=1时,求函数g(x)=f(x)+lnx﹣x的极值;
(Ⅱ)若对任意x∈(0,+∞),不等式f(x)≥0恒成立,求λ的最小值.
已知  为常数,函数
为常数,函数  有两个极值点
有两个极值点  ,
,  (
(  ),则( )
),则( )
 为常数,函数
为常数,函数  有两个极值点
有两个极值点  ,
,  (
(  ),则( )
),则( )
A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
已知函数 , 其图象在
, 其图象在 处的切线过点
处的切线过点 .
.
 , 其图象在
, 其图象在 处的切线过点
处的切线过点 .
.
-
(1) 求a的值;
-
(2) 讨论
 的单调性;
的单调性;
-
(3) 若
 , 关于x的不等式
, 关于x的不等式 在区间
在区间 上恒成立,求
上恒成立,求 的取值范围.
的取值范围.
平面a与平面β平行的条件可以是( )
A . a内有无穷多条直线都与β平行
B . 直线a∥a,a∥B,且直线a不在a内,也不在β内
C . 直线a  a,直线b
a,直线b  B,且a∥B,b∥a
D . a内的任何直线都与β平行
B,且a∥B,b∥a
D . a内的任何直线都与β平行
 a,直线b
a,直线b  B,且a∥B,b∥a
D . a内的任何直线都与β平行
B,且a∥B,b∥a
D . a内的任何直线都与β平行
如图,已知正方形ABCD的边长为1,E在CD延长线上,且DE=CD.动点P从点A出发沿正方形ABCD的边按逆进针方向运动一周回到A点,其中  =λ
=λ  +μ
+μ  ,则下列命题正确的是.(填上所有正确命题的序号)
,则下列命题正确的是.(填上所有正确命题的序号)
 =λ
=λ  +μ
+μ  ,则下列命题正确的是.(填上所有正确命题的序号)
,则下列命题正确的是.(填上所有正确命题的序号) ①当点P为AD中点时,λ+μ=1;
②λ+μ的最大值为3;
③若y为给定的正数,则一存在向量  和实数x,使
和实数x,使  =x
=x  +y
+y  .
.

已知集合 ,
,  , 则
, 则 ( )
( )
 ,
,  , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知数列 是等比数列,且
是等比数列,且 ,
,  .
.
 是等比数列,且
是等比数列,且 ,
,  .
.
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 设
 , 求数列
, 求数列 的前n项和
的前n项和 , 并证明:
, 并证明: .
.
随机变量  服从正态分布
服从正态分布  ,若
,若  ,则
,则  .
.
 服从正态分布
服从正态分布  ,若
,若  ,则
,则  .
.
关于x的不等式ax2-(a+2)x+2<0.
-
(1) 当a=-1时,求不等式的解集;
-
(2) 当a>0时,求不等式的解集.
设 ,
,  是夹角为
是夹角为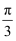 的单位向量,
的单位向量, ,
,  .
.
 ,
,  是夹角为
是夹角为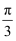 的单位向量,
的单位向量, ,
,  .
.
-
(1) 若
 , 求
, 求 与
与 的夹角;
的夹角;
-
(2) 若
 , 求t的值.
, 求t的值.
已知函数  的定义域为
的定义域为  ,值域为
,值域为  ,则
,则 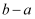 的值不可能是( )
的值不可能是( )
 的定义域为
的定义域为  ,值域为
,值域为  ,则
,则 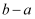 的值不可能是( )
的值不可能是( )
A .  B .
B . 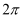 C .
C .  D .
D . 
 B .
B . 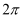 C .
C .  D .
D . 
下列四个命题一定正确的是( )
A . 算法的三种基本结构是顺序结构、条件结构,循环结构
B . 用样本频率分布估计总体频率分布的过程中,总体容量越大,估计越精确
C . 一组数据的方差为3,将这组数据中的每一个数据都扩大到原来的3倍,所得的新数据组的方差还是3
D . 有50件产品编号从1到50,现在从中抽取5件检验,用系统抽样确定所抽取的编号为5,15,20,35,40
如图所示,程序框图(算法流程图)的输出结果是( )

A . 34
B . 55
C . 78
D . 89
若  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A . -4
B . -2
C . 0
D . 2
多项式x3+bx2+cx+d适合于下列三条件:
(1)被x﹣1整除;
(2)被x﹣3除时余2;
(3)被x+2除时与被x﹣2除时的余数相等,求b,c,d的值.
用1,2,3,4,5,6组成六位数(没有重复数字),在任意相邻两个数字的奇偶性不同的条件下,1和2相邻的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
根据以往的经验,某工程施工期间的降水量X(单位:mm)对工期的影响如下表:

历年气象资料表明,该工程施工期间降水量X小于300,700,900的概率分别为0.3,0.7,0.9,求:
(1)工期延误天数Y的均值与方差;
(2)在降水量X至少是300的条件下,工期延误不超过6天的概率.
交通管理部门为了解机动车驾驶员(简称驾驶员)对某新法规的知晓情况,对甲、乙、丙、丁四个社区做分层抽样调查。假设四个社区驾驶员的总人数为![]() ,其中甲社区有驾驶员96人。若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数
,其中甲社区有驾驶员96人。若在甲、乙、丙、丁四个社区抽取驾驶员的人数分别为12,21,25,43,则这四个社区驾驶员的总人数![]() 为( )
为( )
A、101 B、808 C、1212 D、2012
下列问题可以设计成循环语句计算的有
① 求![]() 的和; ② 比较
的和; ② 比较![]() 两个数的大小;
两个数的大小;
③ 对于分段函数,要求输入自变量,输出函数值; ④ 求平方值小于![]() 的最大整数.
的最大整数.
A.![]() 个 B.
个 B.![]() 个 C.
个 C.![]() 个 D.
个 D.![]() 个
个
最近更新
- 小峰和小刚阅读试剂标签后发现,市场销售的高锰酸钾晶体纯度高达99.5%,含水量可以忽略不计。为探究“试管放置方式对高锰酸
- (2015届江苏淮安中考)阅读下面文章。完成后面题目 最美的对视 孙道荣 ①她久久凝视着,凝视着。 ②站在她面前的,是一
- 一组数据 -1,-2,3,4,5,则该组数据的极差是() A. 7 B. 6
- 下列各组词语中,加点字的注音全都正确的一组是( ) A.胆怯(què) 剜(wān)心 岑(cén)
- 下图表示出生率、死亡率和种群密度的关系,据此分析得出的正确表述是 ( )A.在K/2时控制有害动物最有效 B.
- 传统文化中的许多东西常常会出现优弊并存、瑕瑜互见的现象,因此鲁迅提出要“择取中国的遗产,融合新机”,这就是说,我们在文化
- 坚持人民民主专政是社会主义现代化建设的政治保证。从人民民主的角度,其政治保证作用主要体现在( ) ①确保人民当家作主的地
- 下列叙述正确的是 ( )A.250C 101KPa条件下,32gO2占有的体积约为22.4L B.标准状况下,
- 下列关于盐类水解反应说法正确的是A.任何盐都可发生水解反应B.盐只能发生水解反应而不能发生其他反应C.盐水解反应肯定能破
- 函数f(x)=x|x+a|+b是奇函数的充要条件是…()A.ab=0 B.a+b=0
- (08南京市一模)右图是《1933―1936年中国轻工业年(月)平均指数增长表》。它所示经济发展状况的主要原因有(
- 改变一生的闪念(19分) ①这是我的老师的故事,至今珍藏在我心里,让我明白在人世间,其实不应该放过每一个能够帮助别人的机
- 乙醛在氧化铜催化剂存在的条件下,可以被空气氧化成乙酸。依据此原理设计实验制得并在试管C中收集到少量乙酸溶液(如图所示:试
- 右图是反射弧示意图,其中E表示感受器、A表示效应器。以下叙述中正确的是 ( )
- 写作 假如你是Daniel,请根据下列表格中的要点写一封推荐信,推荐你班的Simon 为本年度的青年奖获得者。姓 名 S
- 双链RNA在生物体内是存在的,是一种自然现象,经酶切后会形成很多小片段,这些小片段 一旦与mRNA中的同源序列互补结合,
- 读下面的调查数据统计,回答问题。 27.从图中汉字书写的现状可以得出怎样的结论?(不出现数字,字数10--20) 28
- 用NaOH固体配制1mol/L NaOH溶液,在下列仪器中要用到的是①托盘天平 ②量筒③容量瓶 ④滤纸⑤烧杯⑥玻璃棒 ⑦
- 是否存在实数a使得集合A={y|ay2-3y+2=0,aR}中的元素至多只有一个?若存在,求出实数a的值的集合;若不存在
- (2012年合肥质检)如图所示,小球甲从倾角θ=30°的光滑斜面上高h=5 cm的A点由静止释放,同时小球乙自C点以速



