高中 数学
若全集U={﹣1,0,1,2},P={x∈Z|x2﹣x﹣2<0},则∁UP=( )
A . {0,1}
B . {0,﹣1}
C . {﹣1,2}
D . {﹣1,0,2}
改革开放以来,人们的支付方式发生了巨大转变.近年来,移动支付已成为主要支付方式之一.为了解某校学生上个月A,B两种移动支付方式的使用情况,从全校学生中随机抽取了100人,发现样本中A,B两种支付方式都不使用的有5人,样本中仅使用A和仅使用B的学生的支付金额分布情况如下:
|
支付方式 | (0,1000] | (1000,2000] | 大于2000 |
| 仅使用A | 18人 | 9人 | 3人 |
| 仅使用B | 10人 | 14人 | 1人 |
(Ⅰ)从全校学生中随机抽取1人,估计该学生上个月A,B两种支付方式都使用的概率;
(Ⅱ)从样本仅使用A和仅使用B的学生中各随机抽取1人,以X表示这2人中上个月支付金额大于1000元的人数,求X的分布列和数学期望;
(Ⅲ)已知上个月样本学生的支付方式在本月没有变化.现从样本仅使用A的学生中,随机抽查3人,发现他们本月的支付金额都大于2000元.根据抽查结果,能否认为样本仅使用A的学生中本月支付金额大于2000元的人数有变化?说明理由.
如图,在边长为a的等边三角形ABC中,圆D1与△ABC相切,圆D2与圆D1相切且与AB,AC相切,…,圆Dn+1与圆Dn相切且与AB,AC相切,依次得到圆D3 , D4 , …,Dn.设圆D1 , D2 , …,Dn的面积之和为 , (
, ( ),则
),则 ( )
( )
 , (
, ( ),则
),则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若直线x﹣y+m=0将圆C:x2+y2﹣2x﹣1=0分成两部分的圆弧长之比是1:2,则m=( )
A . 0
B . ﹣2
C . 0或﹣2
D . 1
已知点  ,
,  ,位于
,位于  轴上方的点
轴上方的点  是椭圆
是椭圆  上的动点,且直线
上的动点,且直线  与直线
与直线  的斜率之积为
的斜率之积为 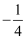 .动直线
.动直线  与直线
与直线  的倾斜角互补,交
的倾斜角互补,交  于
于  ,
,  两点
两点  ,设
,设  关于
关于  轴的对称点为点
轴的对称点为点  .
.
 ,
,  ,位于
,位于  轴上方的点
轴上方的点  是椭圆
是椭圆  上的动点,且直线
上的动点,且直线  与直线
与直线  的斜率之积为
的斜率之积为 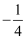 .动直线
.动直线  与直线
与直线  的倾斜角互补,交
的倾斜角互补,交  于
于  ,
,  两点
两点  ,设
,设  关于
关于  轴的对称点为点
轴的对称点为点  .
.
-
(1) 求椭圆
 的标准方程;
的标准方程;
-
(2) 过点
 分别作椭圆
分别作椭圆  的切线
的切线  交于点
交于点 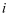 .若当点
.若当点  移动时,始终保持
移动时,始终保持  ,证明:
,证明: 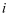 在一条定直线上.
在一条定直线上.
如图,已知AB为⊙O的直径,C,F为⊙O上的两点,OC⊥AB,过点F作⊙O的切线FD交AB的延长线于点D,连接CF交AB于点E.求证:DE2=DA•DB.

甲、乙两地相距12km.A车、B车先后从甲地出发匀速驶向乙地.A车从甲地到乙地需行驶15min;B车从甲地到乙地需行驶10min.若B车比A车晚出发2min:
-
(1) 分别写出A,B两车所行路程关于A车行驶时间的函数关系式;
-
(2) A,B两车何时在途中相遇?相遇时距甲地多远?
若△ABC的内角A,B,C的对边分别为a,b,c,已知c=2,C= 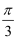 .
.
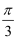 .
.
-
(1) 若b=
 ,求角B;
,求角B;
-
(2) 若sinC+sin(B﹣A)=2sin2A,求△ABC的面积.
已知不等式|x+2|+|x﹣2|<18的解集为A.
-
(1) 求A;
-
(2) 若∀a,b∈A,x∈(0,+∞),不等式a+b<x
 +m恒成立,求实数m的取值范围.
+m恒成立,求实数m的取值范围.
在平面直角坐标系  中,已知圆M过坐标原点O且圆心在曲线
中,已知圆M过坐标原点O且圆心在曲线 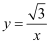 上.
上.
 中,已知圆M过坐标原点O且圆心在曲线
中,已知圆M过坐标原点O且圆心在曲线 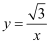 上.
上.
-
(1) 求圆M面积的最小值;
-
(2) 设直线
 与圆M交于不同的两点C、D,且
与圆M交于不同的两点C、D,且  ,求圆M的方程;
,求圆M的方程;
-
(3) 设直线
 与(2)中所求圆M交于点E、F,P为直线
与(2)中所求圆M交于点E、F,P为直线  上的动点,直线
上的动点,直线  ,
,  与圆M的另一个交点分别为G,H,求证:直线
与圆M的另一个交点分别为G,H,求证:直线  过定点.
过定点.
已知函数  ,则函数f(x)的表达式为( )
,则函数f(x)的表达式为( )
 ,则函数f(x)的表达式为( )
,则函数f(x)的表达式为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数  ,则满足
,则满足  的实数x的取值范围是( )
的实数x的取值范围是( )
 ,则满足
,则满足  的实数x的取值范围是( )
的实数x的取值范围是( )
A .  B .
B . 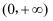 C .
C .  D .
D . 
 B .
B . 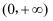 C .
C .  D .
D . 
 是定义在
是定义在  上的函数,若
上的函数,若  是奇函数,
是奇函数,  是偶函数,函数
是偶函数,函数  ,则( )
,则( )
A .  B . 当
B . 当  时,
时,  C .
C .  D .
D . 
 B . 当
B . 当  时,
时,  C .
C .  D .
D . 
如图,在三棱柱ABC﹣A1B1C1中,AA1⊥平面ABC,∠ACB=90°,CA=CB=CC1=1,则直线A1B与平面BB1C1C所成角的正弦值为

如图所示,在平面四边形  中,
中,  ,在
,在  中,角A,B,C的对应边分别为a,b,c,若
中,角A,B,C的对应边分别为a,b,c,若  ,则
,则  的面积为.
的面积为.
 中,
中,  ,在
,在  中,角A,B,C的对应边分别为a,b,c,若
中,角A,B,C的对应边分别为a,b,c,若  ,则
,则  的面积为.
的面积为. 
已知椭圆C1 , 抛物线C2的焦点均在x轴上,C1的中心和C2的顶点均为原点O,从每条曲线上各取两个点,其坐标分别是(3,一2  ),(一2,0),(4,一4),(
),(一2,0),(4,一4),(  ).
).
 ),(一2,0),(4,一4),(
),(一2,0),(4,一4),(  ).
). (Ⅰ)求C1 , C2的标准方程;
(Ⅱ)是否存在直线L满足条件:①过C2的焦点F;②与C1交与不同的两点M,N且满足  ?若存在,求出直线方程;若不存在,说明理由.
?若存在,求出直线方程;若不存在,说明理由.
下列说法错误的是( )
A . 在回归分析中,回归直线始终过样本点( x1 , y1 ),( x2 , y2 ),…,( xn , yn ) 的中心(  )
B . 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于0
C . 在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D . 在线性回归模型中,相关指数R2越接近于1,说明回归的效果越好
)
B . 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于0
C . 在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D . 在线性回归模型中,相关指数R2越接近于1,说明回归的效果越好
 )
B . 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于0
C . 在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D . 在线性回归模型中,相关指数R2越接近于1,说明回归的效果越好
)
B . 若两个具有线性相关关系的变量的相关性越强,则线性相关系数r的值越接近于0
C . 在残差图中,残差点分布的水平带状区域越窄,说明模型的拟合精度越高
D . 在线性回归模型中,相关指数R2越接近于1,说明回归的效果越好
如图所示的三棱锥 中,
中, 面
面 ,
,  ,
,  , 则该三棱锥的外接球的表面积为( )
, 则该三棱锥的外接球的表面积为( )
 中,
中, 面
面 ,
,  ,
,  , 则该三棱锥的外接球的表面积为( )
, 则该三棱锥的外接球的表面积为( )
A .  B . 27π
C . 54π
D . 108π
B . 27π
C . 54π
D . 108π
 B . 27π
C . 54π
D . 108π
B . 27π
C . 54π
D . 108π
.已知数列![]() 的前
的前![]() 项和为
项和为![]() ,且满足
,且满足![]() ,若不等式
,若不等式![]() 对任意的正整数
对任意的正整数![]() 恒成立,则整数
恒成立,则整数![]() 的最大值为( )
的最大值为( )
A. 3 B. 4 C. 5 D. 6
若变量x,y满足约束条件 且z=2x+y的最大值和最小值分别为m和n,则m-n=
且z=2x+y的最大值和最小值分别为m和n,则m-n=
(A)5 (B)6 (C)7 (D)8
最近更新
- 黄河是我国的母亲河,但如今黄河已经成为世界罕见的“悬河”。治理黄河最根本的措施 是 。 ( ) A
- 下图是世界上最早的纸币“交子”,它的出现直接反映了北宋 A.农业生产的新气象
- 已知等比数列中,则其前3项的和的取值范围是()(A) (B) (C)
- Itwas so dark in the theatre that I could hardly ________ m
- 在长期的生产活动中,我国北方农民总结出“白露早,寒露迟,秋分种麦正当时”的农谚。这说明 A.人可以认识规律 B.
- 下列三种生物学现象: ①给小白鼠注射一定量的胰岛素后,小白鼠休克 ②当细菌进入人体后,机体产生特异性的抗体与之结合,从而
- 把直线y=-2x+m向左平移5个单位后,与直线y=2x+4的交点在x轴上,则m的值是 .
- 如果在一个种群中,基因型AA的比例占25%,基因型Aa的比例为50%,基因型aa的比例占25%。已知基因型aa的个体失去
- 有蓝和黑两个墨水瓶,但现在却错把蓝墨水装在了黑墨水瓶中,黑墨水错装在了蓝墨水瓶中,要求将其互换,请你设计算法解决这一问题
- 若,则下列不等式成立的是( ) A. B. C. D.
- 某植株的一条染色体发生缺失突变,获得该缺失染色体的花粉不育,缺失染色体上具有红色显性基因B,正常染色体上具有白色隐性基因
- 病毒不能独立生活,必须生活在 A.植物的枯枝落叶中 B.动物的遗体中 C.生物活细胞中
- 第二节:阅读下面61到65几段文字,为它们从A到F中选出适当的标题。注意:有一个标题是多余的。 A.The most c
- 推动社会主义文化大发展大繁荣,必须大力建设社会主义核心价值体系。这是因为,社会主义核心价值体系是( ) ①社会主义精神
- 如图,已知中,,,,是边上的中点,是边上的点(不与端点重合),是边上的点,且∥,延长与直线相交于点,点是延长线上的点,且
- 已知:2H2(g)+ O2(g)=2H2O(l) ΔH=-571.6KJ· mol-1CH4(g)
- 足量的浓H2SO4与mg铜反应得到标准状况下的SO2 nL,则被还原的H2SO4是( ) A.m/64 mol
- 目前世界上仍有13亿贫因人口,8亿人忍受着饥饿,8000万人完全不能享受医疗服务,超过2.6亿的人不能上学,第三世界国家
- 下列反应不属于取代反应的是( )A.CHCl3+Cl2CCl4+HClB.CH3CH3+2Br2CH2BrCH2B
- 对于进行有性生殖的生物体来说,维持每种生物前后代体细胞中染色体数目恒定的生理作用是( ) A.有丝分裂和无丝分
 交付金额(元)
交付金额(元)


