高中 数学
从 中任取2个不同的数
中任取2个不同的数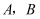 , 则
, 则 的概率是( )
的概率是( )
 中任取2个不同的数
中任取2个不同的数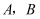 , 则
, 则 的概率是( )
的概率是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若两条直线ax+2y+6=0与x+(a﹣1)y+(a2﹣1)=0平行,则a的取值集合是( )
A . {﹣1,2}
B . {﹣1}
C . {2}
D . { }
}
 }
}
下列叙述正确的是( )
A . 命题“p且q”为真,则  恰有一个为真命题
B . 命题“已知
恰有一个为真命题
B . 命题“已知  ,则“
,则“  ”是“
”是“  ”的充分不必要条件”
C . 命题
”的充分不必要条件”
C . 命题  都有
都有  ,则
,则  ,使得
,使得  D . 如果函数
D . 如果函数  在区间
在区间  上是连续不断的一条曲线,并且有
上是连续不断的一条曲线,并且有  ,那么函数
,那么函数  在区间
在区间  内有零点
内有零点
 恰有一个为真命题
B . 命题“已知
恰有一个为真命题
B . 命题“已知  ,则“
,则“  ”是“
”是“  ”的充分不必要条件”
C . 命题
”的充分不必要条件”
C . 命题  都有
都有  ,则
,则  ,使得
,使得  D . 如果函数
D . 如果函数  在区间
在区间  上是连续不断的一条曲线,并且有
上是连续不断的一条曲线,并且有  ,那么函数
,那么函数  在区间
在区间  内有零点
内有零点
给出下列命题:
 存在每个面都是直角三角形的四面体;
存在每个面都是直角三角形的四面体;  若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;
若三棱锥的三条侧棱两两垂直,则其三个侧面也两两垂直;  棱台的侧棱延长后交于一点;
棱台的侧棱延长后交于一点;  用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;其中正确命题的个数是( )
用一个平面去截棱锥,棱锥底面和截面之间的部分是棱台;其中正确命题的个数是( )
A . 1
B . 2
C . 3
D . 4
已知A、B为抛物线  上的不同的两点,线段
上的不同的两点,线段  中点为P,若
中点为P,若  ,则点P到x轴距离的最小值为.
,则点P到x轴距离的最小值为.
 上的不同的两点,线段
上的不同的两点,线段  中点为P,若
中点为P,若  ,则点P到x轴距离的最小值为.
,则点P到x轴距离的最小值为.
以双曲线  的右焦点为圆心,且与双曲线的渐近线相切的圆的方程为.
的右焦点为圆心,且与双曲线的渐近线相切的圆的方程为.
 的右焦点为圆心,且与双曲线的渐近线相切的圆的方程为.
的右焦点为圆心,且与双曲线的渐近线相切的圆的方程为.
已知{an}是等差数列,a1+a3+a5=99,a2+a4+a6=93,Sn表示{an}的前n项和,则使Sn达到最大值的n是( )
A . 18
B . 19
C . 20
D . 21
已知定义域为R的函数 , 若关于x的方程
, 若关于x的方程 有3个不同的实根
有3个不同的实根 , 则
, 则 等于( )
等于( )
 , 若关于x的方程
, 若关于x的方程 有3个不同的实根
有3个不同的实根 , 则
, 则 等于( )
等于( )
A . 13
B .  C . 5
D .
C . 5
D . 
 C . 5
D .
C . 5
D . 
小明参加某项测试,该测试一共3道试题,每道试题做对得5分,做错得0分,没有中间分,小明答对第1,2题的概率都是 , 答对第3题的概率是
, 答对第3题的概率是 , 则小明答完这3道题的得分期望为( )
, 则小明答完这3道题的得分期望为( )
 , 答对第3题的概率是
, 答对第3题的概率是 , 则小明答完这3道题的得分期望为( )
, 则小明答完这3道题的得分期望为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
若三棱锥P﹣ABC的最长的棱PA=2,且各面均为直角三角形,则此三棱锥的外接球的体积是.
已知P , A , B , C是半径为2的球面上的点,  ,
,  ,点B在AC上的射影为D , 则三棱锥
,点B在AC上的射影为D , 则三棱锥  体积的最大值是
体积的最大值是
 ,
,  ,点B在AC上的射影为D , 则三棱锥
,点B在AC上的射影为D , 则三棱锥  体积的最大值是
体积的最大值是
 的展开式中常数项为( )
的展开式中常数项为( )
A .  B .
B .  C .
C .  D . 105
D . 105
 B .
B .  C .
C .  D . 105
D . 105
在 中,角A,B,C所对的边分别为a,b,c,且满足
中,角A,B,C所对的边分别为a,b,c,且满足 .
.
 中,角A,B,C所对的边分别为a,b,c,且满足
中,角A,B,C所对的边分别为a,b,c,且满足 .
.
-
(1) 求角B的值;
-
(2) 若
 ,
,  的面积为
的面积为 , 求
, 求 边上中线
边上中线 的长.
的长.
已知  对于任意
对于任意  恒成立,则实数a的最大值为( )
恒成立,则实数a的最大值为( )
 对于任意
对于任意  恒成立,则实数a的最大值为( )
恒成立,则实数a的最大值为( )
A . 0
B . 1
C .  D .
D . 
 D .
D . 
“等式![]() 成立”是“
成立”是“![]() 成等差数列”的
成等差数列”的
A.充分而不必要条件 B.必要而不充分条件
C.充分必要条件 D.既不充分又不必要条件
已知函数![]() ,对
,对![]() ,使得
,使得![]() 成立,则
成立,则![]() 的取值范围是( )
的取值范围是( )
A.![]() B.
B.![]()
C.![]() D.
D.![]()
![]()
![]()
已知![]() 是由正数组成的等比数列,
是由正数组成的等比数列,![]() 表示
表示![]() 的前
的前![]() 项的和.若
项的和.若![]() ,
,![]() ,则
,则![]() 的值是( )
的值是( )
A.511 B.1023 C.1533 D.3069
已知函数![]()
(1)解不等式![]() .
.
(2)若关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() ,求实数
,求实数![]() 的取值范围.
的取值范围.
数列![]() 各项均为正数,其前
各项均为正数,其前![]() 项和为
项和为![]() ,且满足
,且满足![]() .
.
(Ⅰ)求证数列![]() 为等差数列,并求数列
为等差数列,并求数列![]() 的通项公式;
的通项公式;
(Ⅱ)设![]() , 求数列
, 求数列![]() 的前n项和
的前n项和![]() ,并求使
,并求使![]() 对所有的
对所有的![]() 都成立的最大正整数m的值.
都成立的最大正整数m的值.
已知动点![]() 在抛物线
在抛物线![]() 上,过点
上,过点![]() 作
作![]() 轴的垂线,垂足为
轴的垂线,垂足为![]() ,动点
,动点![]() 满足
满足![]() .(1)求动点
.(1)求动点![]() 的轨迹
的轨迹![]() 的方程;(2)点
的方程;(2)点![]() ,过点
,过点![]() 且斜率为
且斜率为![]() 的直线交轨迹
的直线交轨迹![]() 于
于![]() 两点,设直线
两点,设直线![]() 的斜率为
的斜率为![]() ,求
,求![]() 的值.
的值.
最近更新
- After a knock at the door, the boy heard his mother’s voice
- 哲学的基本问题是 A.物质和意识的辩证关系 B.个人与社会的关系 C.
- --Did you hear something? --No. I ______ but I ______ anythi
- 读下图,回答9-10题。9. 若甲乙丙代表三大类岩石,箭头表示地质作用,下列说法正确的是 A.①可表示风
- .下列词语中加点的字,读音全都正确的一组是 ( ) A.击柝(t
- 下列有关内容的叙述中,体现利用DNA分子杂交原理的是() ①观察DNA在细胞中的分布 ②检测目的基因是否
- 2015年2月,中共中央、国务院发布的《关于加大改革创新力度和加快农业现代化建设的若干意见》要求:将农村的土地经营权从原
- He could do nothing except __________ TV. A. watch B.w
- 各级政府的财政收入和支出正在逐渐向社会公开,让群众看明白、能监督。下列款项属于财政收入的有 ①个人所得税税款 ②民营企业
- 下列句中加点的熟语,使用不恰当的一句是 A.每天从开市到收市,他的目光就一直盯着这只走势不瘟不火的股票,一遍一遍地推算自
- 选择恰当的试剂或方法除去括号内的杂质。
- 读“某电子产品生命周期模型图”。产品的生命周期理论能够解释产业转移现象,下列叙述正确的是A.该产业转移路径是由丙国一乙国
- 阅读下面的文字,用三个词语分别概括苏州水、苏州话和昆曲表现形式的特点。 当年白居易做苏州刺史,曾写下“绿浪东西南
- 阅读下文,完成文后各题。 每年农历七月初七是中国民间传统节日“七夕”,即中国传统的情人节。媒体给予了相当热情的关注,商家
- 读“中国气候类型分布图”,回答下列各题。14.我国气候特征的叙述,正确的有( ) A.气候的海洋性强 B.气候
- 下列划线字拼音全对的一项是( )A.溃退(guì) 舀水(yǎ0) 白洋淀(dìan) 寒噤
- I thought she was famous, but none of my friends have ______
- 下列各组词语中,有错别字的一组是( )A、追本溯源 正本清源 重蹈覆辙 无以复加B、原形毕露 形象
- 从C、H、O、N、S这5种元素中选择恰当的元素,用离子符号或化学式填空(答案有多种的只需要写出一种即可)。空气中含量第二
- 为了保护鱼类资源不受破坏,并能持续地获得最大捕鱼量,根据种群增长的S型曲线,应使被捕鱼群的种群数量保持在K/2水平。这是



