高中 数学
已知数列  满足
满足  ,且
,且  ,则
,则  .
.
 满足
满足  ,且
,且  ,则
,则  .
.
曲线 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
 在点
在点 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数f(x)=e2x(ax2+2x﹣1),a∈R.
(Ⅰ)当a=4时,求证:过点P(1,0)有三条直线与曲线y=f(x)相切;
(Ⅱ)当x≤0时,f(x)+1≥0,求实数a的取值范围.
复数  的共轭复数的虚部是( )
的共轭复数的虚部是( )
 的共轭复数的虚部是( )
的共轭复数的虚部是( )
A .  B .
B .  C . -1
D . 1
C . -1
D . 1
 B .
B .  C . -1
D . 1
C . -1
D . 1
二项式  的展开式中各项系数之和为;该展开式中的常数项为.(用数字作答)
的展开式中各项系数之和为;该展开式中的常数项为.(用数字作答)
 的展开式中各项系数之和为;该展开式中的常数项为.(用数字作答)
的展开式中各项系数之和为;该展开式中的常数项为.(用数字作答)
已知函数  的图象上相邻的一个最大值点与对称中心分别为
的图象上相邻的一个最大值点与对称中心分别为  ,
,  ,则函数
,则函数  的单调增区间为( )
的单调增区间为( )
 的图象上相邻的一个最大值点与对称中心分别为
的图象上相邻的一个最大值点与对称中心分别为  ,
,  ,则函数
,则函数  的单调增区间为( )
的单调增区间为( )
A .  ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
 ,
,  B .
B .  ,
,  C .
C .  ,
,  D .
D .  ,
, 
从双曲线 的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|-|MT|与b-a 的大小关系为 ( )
的左焦点F引圆x2+y2=a2的切线,切点为T,延长FT交双曲线右支于P点,若M为线段FP的中点,O为坐标原点,则|MO|-|MT|与b-a 的大小关系为 ( ) 
A . |MO|-|MT|>b-a
B . |MO|-|MT|=b-a
C . |MO|-|MT|<b-a
D . 不确定
在 中,已知
中,已知 ,
,  ,
,  ,
, 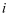 为
为 的内心,
的内心, 的延长线交AB于点D,则
的延长线交AB于点D,则 的外接圆的面积为,
的外接圆的面积为, .
.
 中,已知
中,已知 ,
,  ,
,  ,
, 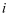 为
为 的内心,
的内心, 的延长线交AB于点D,则
的延长线交AB于点D,则 的外接圆的面积为,
的外接圆的面积为, .
.
已知数列  的前n项和为
的前n项和为  ,向量
,向量  ,
,  满足条件a⊥b,
满足条件a⊥b,
 的前n项和为
的前n项和为  ,向量
,向量  ,
,  满足条件a⊥b,
满足条件a⊥b,
-
(1) 求数列
 的通项公式;
的通项公式;
-
(2) 设
 ,求数列
,求数列  的前n项和
的前n项和  .
.
在△ABC中,若a=7,b=3,c=8,则其面积等于( )
A . 12
B .  C . 28
D .
C . 28
D . 
 C . 28
D .
C . 28
D . 
已知A、B、C是抛物线y2=2px(p>0)上三个不同的点,且AB⊥AC.

(Ⅰ)若A(1,2),B(4,﹣4),求点C的坐标;
(Ⅱ)若抛物线上存在点D,使得线段AD总被直线BC平分,求点A的坐标.
若函数  有3个零点,则实数
有3个零点,则实数  的取值范围是( )
的取值范围是( )
 有3个零点,则实数
有3个零点,则实数  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知α是第二象限的角,其终边上一点为P(a,  ),且cosα=
),且cosα= 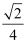 a,则sinα的值等于( )
a,则sinα的值等于( )
 ),且cosα=
),且cosα= 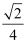 a,则sinα的值等于( )
a,则sinα的值等于( )
A .  B .
B .  C .
C . 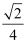 D .
D . 
 B .
B .  C .
C . 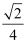 D .
D . 
已知抛物线 的焦点为
的焦点为 , 过
, 过 作一条直线与抛物线
作一条直线与抛物线 及其准线都相交,交点从左到右依次为
及其准线都相交,交点从左到右依次为 , 若
, 若 , 则线段
, 则线段 的中点到
的中点到 轴的距离为.
轴的距离为.
 的焦点为
的焦点为 , 过
, 过 作一条直线与抛物线
作一条直线与抛物线 及其准线都相交,交点从左到右依次为
及其准线都相交,交点从左到右依次为 , 若
, 若 , 则线段
, 则线段 的中点到
的中点到 轴的距离为.
轴的距离为.
冬奥会志愿者有6名男同学,4名女同学.在这10名志愿者中,三名同学来自北京大学,其余7名同学来自北京邮电大学,北京交通大学等其他互不相同的7所大学.现从这10名志愿者中随机选取3名同学,到机场参加活动.(每位同学被选中的可能性相等).
-
(1) 求选出的3名同学是来自互不相同的大学的概率;
-
(2) 设X为选出的3名同学中男同学的人数,求随机变量X的期望和方差.
已知角 的终边经过点
的终边经过点 , 且
, 且 , 则
, 则 的值是( )
的值是( )
 的终边经过点
的终边经过点 , 且
, 且 , 则
, 则 的值是( )
的值是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知椭圆 :
: 的左、右顶点分别为
的左、右顶点分别为 、
、 , 点
, 点 在椭圆
在椭圆 上,且直线
上,且直线 的斜率与直线
的斜率与直线 的斜率之积为
的斜率之积为 .
.
 :
: 的左、右顶点分别为
的左、右顶点分别为 、
、 , 点
, 点 在椭圆
在椭圆 上,且直线
上,且直线 的斜率与直线
的斜率与直线 的斜率之积为
的斜率之积为 .
.
-
(1) 求椭圆
 的方程;
的方程;
-
(2) 若圆
 的切线
的切线 与椭圆
与椭圆 交于
交于 、
、 两点,求
两点,求 的最大值及此时直线
的最大值及此时直线 的斜率.
的斜率.
如图,等边△ABC的边长为10,点P是边AB的中点,Q为BC延长线上一点,CQ:BC=1:2,过P作PE⊥AC于E,连PQ交AC边于D,求DE的长?

从一楼到二楼共有12级台阶,可以一步迈一级也可以一步迈两级,要求8步从一楼到二楼共有( )走法。
A. 12 B. 8. C. 70. D. 66
已知变量x、y满足约束条件![]() ,且z=x+2y的最小值为3,则
,且z=x+2y的最小值为3,则![]() ≥
≥![]() 的概率是( )
的概率是( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
最近更新
- 语文综合性学习(9分) 长城在2004年已列入世界濒危文化遗产名单。某班级在国庆节前夕召开了“爱我长城”主题班会。请你
- x2-10x+25=7;
- 常见金属R与硝酸银溶液反应的化学方程式为R+3AgNO3═3Ag+R(NO3)3,有关该反应的说法正确的是() A.反应
- 下列各项中,属于清康熙帝维护统一多民族国家的史实是( ) ⑴平定三藩,扫除地方割据 ⑵统一台湾,
- 下列说法正确的是 A. 焰火的五彩缤纷是某些金属元素化学性质的展现 B. Na2O中阴、阳离子的个数比为1∶1 C.
- 22.议论文举例论证中有一种“列举法”,即用简短的语句连续举出三个或三个以上的事例证明同一个观点。这样的论证,气势和力度
- 阅读古诗,回答问题。 新晴野望 新晴原野望, 极目五氛垢。 郭门临渡头, 村树连溪口。 白水明田外, 碧峰出山后。
- 关于质点的位移和路程,下列说法中正确的是( )A.位移是矢量,位移的方向即质点运动的方向B.位移的大小不会比路程大
- 已知空气-锌电池的电极反应为:锌片:Zn+2OH――2e-=ZnO+H2O, 石墨:O2+2H2O+ 4e-=4OH-,
- “暖宝宝”取暖片的材料中含有铁粉、水、活性炭、硅石、食盐等,它们组成一个原电池,在反应时释放出热量,铁粉在原电池中充当A
- 已知25℃时有关弱酸的电离平衡常数如下表: 弱酸化学式 HX HY H2CO3 电离平衡常数 7.8╳10-9 3.7╳
- 下列说法正确的是 A.同一纬线上各地地方时相同
- 下列有关神经调节和技术调节的叙述中正确的是( )A.葵花朵朵向太阳属于反射 B.谈虎色变属于人类特
- “玉兔”在月球岩石中发现了铁橄榄石(主要成分是Fe2SiO4),Fe2SiO4中铁元素显+2价,则硅元素的化合价是()
- 用集合的形式表示与下图中的角的终边相同的角的集合.
- 2008年8月8日—24日,第29届奥运会在北京成功举行。回答下题。 体育的发展与经济的发展是分不开的,从产业结构的调整
- 下列各项中,对作品故事情节的叙述不正确的两项是( )(5分) A、玛丝洛娃在聂赫留朵夫第一次到监狱探望她的时候,已经
- 如图所示,在xoy平面直角坐标系的第一象限有射线OA,OA与x轴正方向夹角为30°,OA与y轴所夹区域内有沿y轴负方向的
- 1746年,(英王)乔治二世听取别人的意见,否决了内阁的建议,于是,内阁全体阁员和其他非阁员大臣集体辞职。乔治二世面临政
- 右下图是汽车上的速度表,一辆小汽车以此速度从玉屏驶向贵阳,若玉屏至贵阳约为3.2×105m,则( )



