高中 数学
设l、m、n为不同的直线,α、β为不同的平面,有如下四个命题,其中正确命题的个数是( )
①若α⊥β,l⊥α,则l∥β
②若α⊥β,l⊂α,则l⊥β
③若l⊥m,m⊥n,则l∥n
④若m⊥α,n∥β且α∥β,则m⊥n.
A . 4
B . 3
C . 2
D . 1
已知函数 图象上相邻两条对称轴之间的距离为
图象上相邻两条对称轴之间的距离为 , 则
, 则 =( )
=( )
 图象上相邻两条对称轴之间的距离为
图象上相邻两条对称轴之间的距离为 , 则
, 则 =( )
=( )
A . 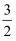 B .
B . 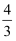 C .
C .  D .
D . 
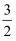 B .
B . 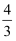 C .
C .  D .
D . 
为普及冬奥知识,某校在各班选拔部分学生进行冬奥知识竞赛. 根据参赛学生的成绩,得到如图所示的频率分布直方图. 若要对40%成绩较高的学生进行奖励,则获奖学生的最低成绩可能为( )

A . 65
B . 75
C . 85
D . 95
函数y=﹣sin(ωx+φ)(ω>0,φ∈(﹣  ,
,  ))的一条对称轴为x=
))的一条对称轴为x= 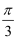 ,一个对称中心为(
,一个对称中心为(  ,0),在区间[0,
,0),在区间[0, 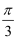 ]上单调.
]上单调.
 ,
,  ))的一条对称轴为x=
))的一条对称轴为x= 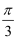 ,一个对称中心为(
,一个对称中心为(  ,0),在区间[0,
,0),在区间[0, 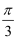 ]上单调.
]上单调.
-
(1) 求ω,φ的值;
-
(2) 用描点法作出y=sin(ωx+φ)在[0,π]上的图象.
集合 , 集合
, 集合 , 若集合
, 若集合 , 则实数a的取值范围是( )
, 则实数a的取值范围是( )
 , 集合
, 集合 , 若集合
, 若集合 , 则实数a的取值范围是( )
, 则实数a的取值范围是( )
A .  B .
B .  C .
C .  D . R
D . R
 B .
B .  C .
C .  D . R
D . R
模长为1的复数x,y,z满足x+y+z≠0,则  的值是.
的值是.
 的值是.
的值是.
体积为1的正方体的内切球的体积是( )
A . 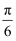 B .
B . 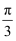 C .
C .  D .
D . 
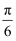 B .
B . 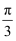 C .
C .  D .
D . 
已知  ,且满足
,且满足  ,则
,则  的值是.
的值是.
 ,且满足
,且满足  ,则
,则  的值是.
的值是.
已知集合  ,
,  ,则
,则  ( )
( )
 ,
,  ,则
,则  ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
集合  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A .  B . {1}
C .
B . {1}
C .  D .
D . 
 B . {1}
C .
B . {1}
C .  D .
D . 
已知 , 则
, 则 ( )
( )
 , 则
, 则 ( )
( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知点P(2,0)及圆C:x2+y2﹣6x+4y+4=0.
-
(1) 设过P直线l1与圆C交于M、N两点,当|MN|=4时,求以MN为直径的圆Q的方程;
-
(2) 设直线ax﹣y+1=0与圆C交于A,B两点,是否存在实数a,使得过点P(2,0)的直线l2垂直平分弦AB?若存在,求出实数a的值;若不存在,请说明理由.
设F1 , F2是双曲线 ﹣y2=1的两个焦点,点P在双曲线上,且
﹣y2=1的两个焦点,点P在双曲线上,且 =0,则|
=0,则| |•|
|•| |的值等于( )
|的值等于( )
 ﹣y2=1的两个焦点,点P在双曲线上,且
﹣y2=1的两个焦点,点P在双曲线上,且 =0,则|
=0,则| |•|
|•| |的值等于( )
|的值等于( )
A . 2
B . 2 C . 4
D . 8
C . 4
D . 8
 C . 4
D . 8
C . 4
D . 8
已知函数  为R上的奇函数,且在
为R上的奇函数,且在  上单调递增,则
上单调递增,则  的值可能是( )
的值可能是( )
 为R上的奇函数,且在
为R上的奇函数,且在  上单调递增,则
上单调递增,则  的值可能是( )
的值可能是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
与向量a=(-5,12)方向相反的单位向量是( )
A . (5,-12)
B . (- 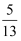 ,
,  )
C . (
)
C . (  ,-
,-  )
D . (
)
D . ( 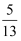 ,-
,-  )
)
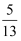 ,
,  )
C . (
)
C . (  ,-
,-  )
D . (
)
D . ( 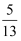 ,-
,-  )
)
已知  ,
,  ,则
,则  的值为.
的值为.
 ,
,  ,则
,则  的值为.
的值为.
已知  :
:  ,
,  :
:  ,若
,若  是
是  的充分不必要条件,求正实数
的充分不必要条件,求正实数  的取值范围.
的取值范围.
 :
:  ,
,  :
:  ,若
,若  是
是  的充分不必要条件,求正实数
的充分不必要条件,求正实数  的取值范围.
的取值范围.
已知数列 




A . 

已知二次函数f(x)=x2+bx+c(其中b,c为实常数).
(Ⅰ)若b>2,且y=f(sinx)(x∈R)的最大值为5,最小值为﹣1,求函数y=f(x)的解析式;
(Ⅱ)是否存在这样的函数y=f(x),使得{y|y=x2+bx+c,﹣1≤x≤0}=[﹣1,0],若存在,求出函数y=f(x)的解析式;若不存在,请说明理由.
(Ⅲ)记集合A={x|f(x)=x,x∈R},B={x|f(f(x))=x,x∈R}.
①若A≠∅,求证:B≠∅;
②若A=∅,判断B是否也为空集.
在等差数列![]() 中,若
中,若![]() 则
则![]() 的最大值为 .
的最大值为 .
最近更新
- 下表反映了我国四个省区煤炭、太阳能、天然气、水四种资源的丰歉程度(★号越多代表资源分布越丰富),据此完成下列问题。21.
- 如图所示,放在水平桌面上的木块A处于静止状态,所挂砝码和托盘的总质量为0.6Kg,弹簧秤的读数为2N。若轻轻取走盘中的部
- 与漫画《未亡羊,先补牢》反映的哲理相近的成语是 A.居安思危 未雨绸缪
- 随着人们生活水平的提高,普通手机的使用已很普遍。下列关于普通手机的说法正确的是( )A.手机既可以发射电磁波,也可
- 判断病毒是生物的主要理由是() A. 能繁殖 B. 能运动 C. 由细胞构成 D. 能呼吸
- 34. (8分)【生物一生物技术实践】 脂肪酶在食品、医药、日化等领域具有广泛应用。工业用脂肪酶通常是通过微生物发酵
- 单项选择 Sit down,please! _____.A. Yes B. Sitdown
- 依次填入下列各句横线处的词语,最恰当的一组是( ) ①一些心理学家认为,在非常紧急和恐怖的情况下,人有时能
- 在相同的温度和压强下,4个容器中分别装有4种气体。已知各容器中的气体和容器的容积分别是:a、CO2:100mL;b、O2
- 理论预测以下物质的物理性质,用>、=、<填空: (1)CS2的沸点_________ CO2的沸点。 (2)Cs
- 某生物的卵细胞中含12条染色体,该生物受精卵细胞分裂后形成的子细胞中,染色体数目是 A.12对 B
- 下列各句中,没有语病的一句是 ( ) A.由于我国各地自然环境、生活条件、经
- 12.一个长方体的各顶点均在同一球的球面上,且一个顶点上的三条棱的长分别为1,2,3,则此球的表面积为 .
- 下列变化属于物理变化的是() A. 火箭发射 B. 节日焰火 C. 风力发电 D. 葡萄酿酒
- 2014年3月8日凌晨,马来西亚航空公司吉隆坡飞北京的MH370航班在起飞一个多小时后在雷达上消失,至今没有被发现踪迹.
- 下列各项生命活动属于生物共同特征的是() A. 光合作用 B. 呼吸作用 C. 蒸腾作用 D. 光合作用和蒸腾作用
- 下图漫画《助农》启示我们 ()A.客观与主观具体
- (08年长沙一中一模)已知且函数为的导函数,若为奇函数,则 .
- .胡适曾在《胡适留学日记》里写道:“梁任公为吾国革命第一大功臣,其功在革新吾国之思想界。十五年来,吾国人士所以稍知民族思
- 不同生物含有的核酸种类不同.真核生物同时含有DNA和RNA,病毒体内含有DNA或RNA,下列各种生物中关于碱基、核苷酸种



