高中 数学
设  、
、  为两个不重合的平面,则
为两个不重合的平面,则  的充要条件是( )
的充要条件是( )
 、
、  为两个不重合的平面,则
为两个不重合的平面,则  的充要条件是( )
的充要条件是( )
A .  内有无数条直线与
内有无数条直线与  平行
B .
平行
B .  、
、  垂直于同一平面
C .
垂直于同一平面
C .  、
、  平行于同一条直线
D .
平行于同一条直线
D .  内有两条相交直线与
内有两条相交直线与  平行
平行
 内有无数条直线与
内有无数条直线与  平行
B .
平行
B .  、
、  垂直于同一平面
C .
垂直于同一平面
C .  、
、  平行于同一条直线
D .
平行于同一条直线
D .  内有两条相交直线与
内有两条相交直线与  平行
平行
计算:  ;
; 
 ;
; 
已知等差数列{an}中,a2=3,a5=12,则公差d等于( )
A . 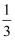 B .
B .  C . 2
D . 3
C . 2
D . 3
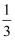 B .
B .  C . 2
D . 3
C . 2
D . 3
已知圆  过
过  ,
,  两点,且圆心
两点,且圆心  在直线
在直线  上.
上.
 过
过  ,
,  两点,且圆心
两点,且圆心  在直线
在直线  上.
上.
-
(1) 求圆
 的方程;
的方程;
-
(2) 若直线
 过点
过点  且被圆
且被圆  截得的线段长为
截得的线段长为 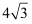 ,求
,求  的方程.
的方程.
《九章算术》是我国古代内容极为丰富的一部数学专著,书中有如下问题:今有女子善织,日增等尺,七日织二十八尺,第二日、第五日、第八日所织之和为十五尺,则第十日所织尺数为( )
A .  B .
B .  C .
C . 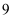 D .
D . 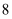
 B .
B .  C .
C . 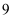 D .
D . 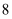
某学校要建造一个面积为10000平方米的运动场.如图,运动场是由一个矩形ABCD和分别以  为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.
为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.
 为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮.
为直径的两个半圆组成.跑道是一条宽8米的塑胶跑道,运动场除跑道外,其他地方均铺设草皮. 
-
(1) 设半圆的半径
 (米),矩形长
(米),矩形长  (米),试建立
(米),试建立  与
与  的函数关系
的函数关系  ;
;
-
(2) 由于条件限制
 ,问当
,问当  取何值时,塑胶跑道的面积最小?
取何值时,塑胶跑道的面积最小?
如图所示,已知A(4,0),B(0,4),从点P(2,0)射出的光线经直线AB反射后再射到直线OB上,最后经直线OB反射后又回到P点,则光线所经过的路程是( )

A . 2  B . 6
C . 3
B . 6
C . 3  D . 2
D . 2 
设  ,
,  均为单位向量且夹角为
均为单位向量且夹角为  ,则“
,则“  ”是“
”是“  为锐角”的( )
为锐角”的( )
 ,
,  均为单位向量且夹角为
均为单位向量且夹角为  ,则“
,则“  ”是“
”是“  为锐角”的( )
为锐角”的( )
A . 充分而不必要条件
B . 必要而不充分条件
C . 充分必要条件
D . 既不充分也不必要条件
已知 , 则a,b,c的大小关系是( )
, 则a,b,c的大小关系是( )
 , 则a,b,c的大小关系是( )
, 则a,b,c的大小关系是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
设函数f(x)=|x|x+bx+c,给出下列4个命题:
①b=0,c>0时,方程f(x)=0只有一个实数根;
②c=0时,y=f(x)是奇函数;
③y=f(x)的图象关于点(0,c)对称;
④方程f(x)=0至多有2个不相等的实数根.
上述命题中的所有正确命题的序号是.
若函数f(x)=2|x﹣1|且f(x)在[m,+∞)上单调递增,则实数m的最小值等于
若  展开式中含
展开式中含  项的系数为21,则实数
项的系数为21,则实数  的值为( )
的值为( )
 展开式中含
展开式中含  项的系数为21,则实数
项的系数为21,则实数  的值为( )
的值为( )
A . 3
B . -3
C . 2
D . -2
如图,四边形  为菱形,
为菱形,  ,
,  面
面  ,
,  ,
,  ,
,  为
为  的中点.
的中点.
 为菱形,
为菱形,  ,
,  面
面  ,
,  ,
,  ,
,  为
为  的中点.
的中点. 
-
(1) 求证:
 平面
平面  ;
;
-
(2) 若
 为线段
为线段  上一点,当三棱锥
上一点,当三棱锥  的体积为
的体积为  时,求
时,求  的值.
的值.
已知向量  ,
,  ,若
,若  ,则实数
,则实数  的值为.
的值为.
 ,
,  ,若
,若  ,则实数
,则实数  的值为.
的值为.
(本小题满分12分)
已知![]() ,
,![]() <θ<π.
<θ<π.
(1) 求t![]() anθ;
anθ;
(2) 求![]() 的值.
的值.
过两直线2x-3y+10=0和3x+4y-2=0的交点,且斜率为![]() 的直线方程为________________.
的直线方程为________________.
把下列推断写成三段论的形式:
y=sin x(x∈R)是周期函数.
已知命题![]() 不等式
不等式![]() 的解集为R;命题
的解集为R;命题![]() :
:![]() 在区间
在区间![]() 上是增函数.若命题“
上是增函数.若命题“![]() ”为假命题,求实数
”为假命题,求实数![]() 的取值范围.
的取值范围.
现有五种不同的颜色要对图形中的四个部分进行着色,要求有公共边
的两块不能用同一种颜色,适合的涂色方法有________种.

设函数![]() 图像上的一个最高点为A,其相邻的一个最低点为B,且|AB|=
图像上的一个最高点为A,其相邻的一个最低点为B,且|AB|=![]() .
.
(1)求![]() 的值;
的值;
(2)设△ABC的内角A、B、C的对边分别为a、b、c,且b+c=2,![]() ,求
,求![]() 的值域.
的值域.
最近更新
- 根据汉语意思完成句子 1.我叔叔不喜欢早饭吃鸡蛋。 Myuncle eggs
- 下列器材或装置中,不是利用连通器原理进行工作的是A 船闸 B 针筒
- 下列反应既是离子反应又是氧化还原反应的是 ( ) A、NaOH溶液和FeSO4溶液
- 下列关于精子与卵细胞结合成合子过程的叙述,正确的是 ① 合子中的遗传物质主要来自染色体 ② 合子中的细胞质主要来自卵细胞
- ______ is impossible if you put your heart into it. A. A
- 一个城管执法人员发现几名小摊贩占道贩卖日用品,不仅影响附近商店的正常营业,还造成了交通阻塞。该城管执法人员依照《城市综合
- 下列实验操作正确的是() A. 熄灭酒精灯 B. 倾倒液体 C. 气体验满 D. 液体过滤
- 图4所示的自行车,从它的结构和使用来看,它应用了许多物理知识。下列有关它的说法中错误的是A.车座的设计应用了压强的知识
- 我们食用的大米,是稻谷种子的( ) A.胚芽 B.胚轴
- He ____ to lend me his bike but I refused, for I didn’t want
- 让杂合子Aa连续自交三代,则第四代中杂合子所占比例为() A.1/4 B.1/8 C.1/16 D
- Ms. Zero was preparing food. Under one of the apple tre
- 下列叙述中不正确的是A.金属的电化腐蚀比化学腐蚀普遍 B.钢铁在干燥空气里不易腐蚀C.用铝质铆钉铆接铁板,铁
- 对组成细胞的有机物描述正确的是()A. 动物乳汁中的乳糖和植物细胞中的纤维素都属于多糖. B. 细胞膜上的脂质主要包括磷
- 下列生活中常见的一些变化,其中属于化学变化的是 A.夏天雪糕慢慢融化 B.潮湿的衣服在空气中变干 C.洗净的铁锅出现锈迹
- 下图为我国华北某城市城区地租分布等值线图(数值:a>b>c),读图完成24-25题。 24.该市重工业不断
- 一次函数y=kx+b中,k、b都是 ,且k ,自变量x的取值范围是 ,当k
- 下列各句中,划线的成语使用恰当的一项是( )(3分) A.他性格比较内向,平时沉默寡言,但是一到课堂上就变得振振有词
- 阅读下面的文字,完成问题。羊皮筏子划过的岁月安福学①在兰州穿城而过的古老黄河上,现代大都市的喧嚣中还保留着一幅令人心醉神
- 植物细胞可以通过渗透作用吸水和失水,将带“皮”的幼嫩的茎纵切后插入两烧杯中,如图所示。已知b侧的细胞壁比a侧的细胞壁薄,



