高中 数学
在  中,内角
中,内角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  ,若
,若  .
.
 中,内角
中,内角  ,
,  ,
,  所对的边分别为
所对的边分别为  ,
,  ,
,  ,若
,若  .
.
-
(1) 求
 ;
;
-
(2) 若
 ,求
,求  面积的最大值.
面积的最大值.
若cos(  )cos(
)cos(  )=
)=  (0<θ<
(0<θ<  ),则sin2θ=.
),则sin2θ=.
 )cos(
)cos(  )=
)=  (0<θ<
(0<θ<  ),则sin2θ=.
),则sin2θ=.
已知双曲线  的两条渐近线互相垂直,则离心率
的两条渐近线互相垂直,则离心率 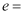 ( )
( )
 的两条渐近线互相垂直,则离心率
的两条渐近线互相垂直,则离心率 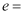 ( )
( )
A .  B .
B .  C . 2
D .
C . 2
D . 
 B .
B .  C . 2
D .
C . 2
D . 
以  为圆心的两圆均过
为圆心的两圆均过  ,与
,与  轴正半轴分别交于
轴正半轴分别交于  ,且满足
,且满足  ,则点
,则点  的轨迹是
的轨迹是
 为圆心的两圆均过
为圆心的两圆均过  ,与
,与  轴正半轴分别交于
轴正半轴分别交于  ,且满足
,且满足  ,则点
,则点  的轨迹是
的轨迹是
A . 直线
B . 圆
C . 椭圆
D . 双曲线
设f(x)=|2﹣x2|,若0<a<b且f(a)=f(b),则a+b的取值范围是( )
A . (0,2)
B . ( , 2)
C . (2,4)
D . (2,2
, 2)
C . (2,4)
D . (2,2 )
)
 , 2)
C . (2,4)
D . (2,2
, 2)
C . (2,4)
D . (2,2 )
)
已知各项均不为零的等差数列 的前n项和为
的前n项和为 ,
,  ,
,  是等比数列,
是等比数列, , 则
, 则 .
.
 的前n项和为
的前n项和为 ,
,  ,
,  是等比数列,
是等比数列, , 则
, 则 .
.
已知A,B是球O的球面上两点,∠AOB=90°,C为该球面上的动点,.若三棱锥O﹣ABC体积的最大值为 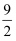 ,则球O的表面积为.
,则球O的表面积为.
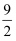 ,则球O的表面积为.
,则球O的表面积为.
设 , 则椭圆
, 则椭圆 的离心率是( )
的离心率是( )
 , 则椭圆
, 则椭圆 的离心率是( )
的离心率是( )
A .  B .
B .  C .
C .  D . 与
D . 与 的取值有关
的取值有关
 B .
B .  C .
C .  D . 与
D . 与 的取值有关
的取值有关
已知曲线C的参数方程为  (α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
 (α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
(α为参数),以直角坐标系原点为极点,Ox轴正半轴为极轴建立极坐标系.
-
(1) 求曲线C的极坐标方程
-
(2) 若直线l的极坐标方程为ρ(sinθ+cosθ)=1,求直线l被曲线C截得的弦长.
已知一个命题P(k),k=2n(n∈N),若n =1,2,…,1000时,P(k)成立,且当 时它也成立,下列判断中,正确的是 ( )
时它也成立,下列判断中,正确的是 ( )
 时它也成立,下列判断中,正确的是 ( )
时它也成立,下列判断中,正确的是 ( )
A . P(k)对k=2013成立
B . P(k)对每一个自然数k成立
C . P(k)对每一个正偶数k成立
D . P(k)对某些偶数可能不成立
阅读如图所示的程序语句,当分别输入  时,输出的值
时,输出的值  .
.
 时,输出的值
时,输出的值  .
. 
若a,b,c成等差数列,则  一定( )
一定( )
 一定( )
一定( )
A . 成等差数列
B . 成等比数列
C . 既成等差数列也成等比数列
D . 既不成等差数列也不成等比数列
若 ,
,  ,
,  , 则a,b,c的大小关系为( ).
, 则a,b,c的大小关系为( ).
 ,
,  ,
,  , 则a,b,c的大小关系为( ).
, 则a,b,c的大小关系为( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
如图,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() (
(![]() )是曲线C:
)是曲线C:![]() 上的n个点,点
上的n个点,点![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() 在x轴的正半轴上,且
在x轴的正半轴上,且![]() 是正三角形(
是正三角形(![]() 是坐标原点)。
是坐标原点)。
(1)求![]() ,
,![]() ,
,![]() 的值,并猜想
的值,并猜想![]() 的表达式;
的表达式;
(2)用数学归纳法证明你的猜想。
 |
如图,已知椭圆![]() 与
与![]() 的中心在坐标原点
的中心在坐标原点![]() ,长轴均为
,长轴均为![]() 且在
且在![]() 轴上,短轴长分别
轴上,短轴长分别
为![]() ,
,![]() ,过原点且不与
,过原点且不与![]() 轴重合的直线
轴重合的直线![]() 与
与![]() ,
,![]() 的四个交点按纵坐标从
的四个交点按纵坐标从
大到小依次为A,B,C,D.记![]() ,△
,△![]() 和△
和△![]() 的面积分别为
的面积分别为![]() 和
和![]() .
.
(Ⅰ)当直线![]() 与
与![]() 轴重合时,若
轴重合时,若![]() ,求
,求![]() 的值;
的值;
(Ⅱ)当![]() 变化时,是否存在与坐标轴不重合的直线l,使得
变化时,是否存在与坐标轴不重合的直线l,使得![]() ?并说明理由.
?并说明理由.
 |
学生的语文、数学成绩均被评定为三个等级,依次为“优秀”“合格”“不合格”.若学生甲的语文、数学成绩都不低于学生乙,且其中至少有一门成绩高于乙,则称“学生甲比学生乙成绩好”.如果一组学生中没有哪位学生比另一位学生成绩好,并且不存在语文成绩相同、数学成绩也相同的两位学生,那么这组学生最多有( )
A.2人 B.3人
C.4人 D.5人
已知f(x)=ax-lnx,x∈(0,e],其中e是自然常数,a∈R.
(1)当a=1时,求f(x)的单调区间和极值;
(2)是否存在实数a,使f(x)的最小值是3,若存在,求出a的值;若不存在,说明理由。
已知函数f(x)=(x2+bx+b)·![]() (b∈R).
(b∈R).
(1)当b=4时,求f(x)的极值;
(2)若f(x)在![]() 区间
区间![]() 上单调递增,求实数b的取值范围.
上单调递增,求实数b的取值范围.
已知函数f(x)=![]() +ln x.
+ln x.
(1)当a=![]() 时,求f(x)在[1,e]上的最大值和最小值;
时,求f(x)在[1,e]上的最大值和最小值;
(2)若函数g(x)=f(x)-![]() x在[1,e]上为增函数,求正实数a的取值范围.
x在[1,e]上为增函数,求正实数a的取值范围.
已知函数 ,若
,若
 ,则
,则 的最小值为( )
的最小值为( )
A. B.
B.  C.
C.  D.
D. 
A.
最近更新
- 下列说法正确的是( )A.凡金属跟非金属元素化合时都形成离子键B.离子化合物中的阳离子,只能是金属离子C.离子化合
- 学校有一台应急备用发电机,内阻为r=1 Ω,升压变压器匝数比为1∶4,降压变压器的匝数比为4∶1,输电线的总电阻为R=4
- 在细菌的作用下,用氨(NH3)处理含甲醇(CH3OH)的工业废水,使其变成无毒的CO2和另一种气体A,从而消除对环境的污
- 在△ABC中,角A,B,C所对的边分别为a,b,c.已知bcos C+ccos B=2b,则=.
- “螳螂捕蝉,黄雀在后。”对该食物链表述正确的是A.蝉→螳螂→黄雀B.蝉←螳螂←黄雀C.柳树←蝉←螳螂←黄雀D.柳树→蝉→
- 同学们在家里洗衣服时,可能都会遇到过这样的情景:当洗衣机没有放平稳时,就跟过飞机一样,产生很大的噪声。为防止洗衣机此种工
- 台湾亲民党主席宋楚瑜率团访问大陆。宋楚瑜的大陆之行属于()A.变革自然的生产实践 B.处理社会关系的实践C.科学实验 D
- 代表中国最广大人民的根本利益,必须始终不渝地坚持遵循社会发展规律与尊重人民历史主体地位的一致性,坚持为崇高理想奋斗与为最
- 已知平面,直线,直线m⊂,则“直线∥”是“∥m”的 [ A.充分不必要条件 B.必要不充
- 若x≥-,函数f(x)=x2+x+a的图象与它的反函数图象有两个不重合的交点的条件是( )A.a<
- 在数3.14,,,,0,,0.10110111011110,中, 无理数有
- 如图所示,A为置于地球赤道上的物体,B为绕地球做椭圆轨道运行的卫星,C为绕地球做圆周运动的卫星,P为B、C两卫星轨道的交
- “大包干,大包干,直来直去不拐弯。保证国家的,留足集体的,剩下都是自己的。”与这一歌谣相关的是 ( ) A、
- She didn't answer the phone.She ___ be asleep. A. couldn't
- Gary Locke, 61, who comes from a Chinesebackground and even
- 下列有关金属冶炼的说法中错误的是( ) A.炼铁中加入焦炭作造渣剂 B.炼钢中吹入氧气作氧化剂 C.电解铝生产中加
- (07年广东卷文)图l是某县参加2007年高考的学生身高条形统计图,从左到右的各条形表示的学生人数依次记为、、…、(如表
- ......
- 如图,边长为1的正方形ABCD绕点A逆时针旋转45°后得到正方形AB1C1D1,边B1C1与CD交于点O,则四边形AB1
- “军人和一切公职人员都由国家支付薪金。这样,一般公民也能当军人、法官、议员了。”这一现象开始于() A.雅典城邦形成时



