高中 数学
设集合 ,分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件
,分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件 ,若事件
,若事件 的概率最大,则n的所有可能值为:( )
的概率最大,则n的所有可能值为:( )
 ,分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件
,分别从集合A和B中随机取一个数a和b,确定平面上的一个点P(a,b),记“点P(a,b)落在直线x+y=n上”为事件 ,若事件
,若事件 的概率最大,则n的所有可能值为:( )
的概率最大,则n的所有可能值为:( )
A . 3
B . 4
C . 3和4
D . 2和5
若0<x<2,则函数  的最大值是.
的最大值是.
 的最大值是.
的最大值是.
在平行六面体ABCD—A1B1C1D1中,M为AC与BD的交点,若 =
= ,
, =
= ,
, =
= .则下列向量中与
.则下列向量中与 相等的向量是( )
相等的向量是( )
 =
= ,
, =
= ,
, =
= .则下列向量中与
.则下列向量中与 相等的向量是( )
相等的向量是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
射击是使用某种特定型号的枪支对各种预先设置的目标进行射击,以命中精确度计算成绩的一项体育运动.射击运动不仅能锻炼身体,而且可以培养细致、沉着、坚毅等优良品质,有益于身心健康.为了度过愉快的假期,感受体育运动的美好,法外狂徒张三来到私人靶场体验射击运动.
-
(1) 已知用于射击打靶的某型号步枪的弹夹中一共有
 发子弹,假设张三每次打靶的命中率均为
发子弹,假设张三每次打靶的命中率均为  ,靶场主规定:一旦出现子弹脱靶或者子弹打光耗尽的现象便立刻停止射击.记标靶上的子弹数量为随机变量
,靶场主规定:一旦出现子弹脱靶或者子弹打光耗尽的现象便立刻停止射击.记标靶上的子弹数量为随机变量  ,求
,求  的分布列和数学期望.
的分布列和数学期望.
-
(2) 张三在休息之余用手机逛
 站刷到了著名电视剧《津门飞鹰》中的经典桥段:中国队长燕双鹰和三合会何五姑玩起了俄罗斯轮盘.这让张三不由得想起了半人半鬼,神枪第一的那句家喻户晓的神话“我赌你的枪里没有子弹”.由此,在接下来的射击体验中,张三利用自己的人脉关系想办法找人更换了一把型号为M1917,弹容为6发的左轮手枪,弹巢中有
站刷到了著名电视剧《津门飞鹰》中的经典桥段:中国队长燕双鹰和三合会何五姑玩起了俄罗斯轮盘.这让张三不由得想起了半人半鬼,神枪第一的那句家喻户晓的神话“我赌你的枪里没有子弹”.由此,在接下来的射击体验中,张三利用自己的人脉关系想办法找人更换了一把型号为M1917,弹容为6发的左轮手枪,弹巢中有  发实弹,其余均为空包弹.现规定:每次射击后,都需要在下一次射击之前填充一发空包弹.假设每次射击相互独立且均随机.在进行
发实弹,其余均为空包弹.现规定:每次射击后,都需要在下一次射击之前填充一发空包弹.假设每次射击相互独立且均随机.在进行  次射击后,记弹巢中空包弹的发数
次射击后,记弹巢中空包弹的发数  .
. (ⅰ)当
 时,探究数学期望
时,探究数学期望  和
和  之间的关系;
之间的关系;(ⅱ)若无论
 取何值,当射击次数达到一定程度后都可近似认为枪中没有实弹(以弹巢中实弹的发数的数学期望为决策依据,当弹巢中实弹的发数的数学期望
取何值,当射击次数达到一定程度后都可近似认为枪中没有实弹(以弹巢中实弹的发数的数学期望为决策依据,当弹巢中实弹的发数的数学期望  时可近似认为枪中没有实弹),求该种情况下最小的射击次数
时可近似认为枪中没有实弹),求该种情况下最小的射击次数  .(参考数据:
.(参考数据:  、
、  )
)
已知双曲线  =1(a>0,b>0)的焦距为2
=1(a>0,b>0)的焦距为2  ,且双曲线的一条渐近线与直线2x+y=0垂直,则双曲线的方程为.
,且双曲线的一条渐近线与直线2x+y=0垂直,则双曲线的方程为.
 =1(a>0,b>0)的焦距为2
=1(a>0,b>0)的焦距为2  ,且双曲线的一条渐近线与直线2x+y=0垂直,则双曲线的方程为.
,且双曲线的一条渐近线与直线2x+y=0垂直,则双曲线的方程为.
函数f(x)=loga|x|在(0,+∞)上单调递减,则f(﹣2) f(a+1)(填“<”,“=”,“>”之一).
已知△ABC的内角A,B,C的对边分别为a、b、c,满足 

-
(1) 求角B的大小;
-
(2) 若a=1,b2=ac,求△ABC的面积.
如图,在正方体ABCD﹣A1B1C1D1中,E为DD1的中点.求证:

-
(1) BD1∥平面EAC;
-
(2) 平面EAC⊥平面AB1C.
对于给定的正整数k,若数列{an}满足 

对任意正整数n(n> k) 总成立,则称数列{an} 是“P(k)数列”.
-
(1) 证明:等差数列{an}是“P(3)数列”;
-
(2) 若数列{an}既是“P(2)数列”,又是“P(3)数列”,证明:{an}是等差数列.
已知等差数列 , 若存在有穷等比数列
, 若存在有穷等比数列 , 其中
, 其中 , 公比为
, 公比为 , 满足
, 满足 , 其中
, 其中 , 则称数列
, 则称数列 为数列
为数列 的长度为
的长度为 的“等比伴随数列”.
的“等比伴随数列”.
 , 若存在有穷等比数列
, 若存在有穷等比数列 , 其中
, 其中 , 公比为
, 公比为 , 满足
, 满足 , 其中
, 其中 , 则称数列
, 则称数列 为数列
为数列 的长度为
的长度为 的“等比伴随数列”.
的“等比伴随数列”.
-
(1) 数列
 的通项公式为
的通项公式为 , 写出数列
, 写出数列 的一个长度为
的一个长度为 的“等比伴随数列”;
的“等比伴随数列”;
-
(2) 等差数列
 的公差为
的公差为 , 若
, 若 存在长度为
存在长度为 的“等比伴随数列”
的“等比伴随数列” , 其中
, 其中 , 求
, 求 的最大值;
的最大值;
-
(3) 数列
 的通项公式为
的通项公式为 , 数列
, 数列 为数列
为数列 的长度为
的长度为 的“等比伴随数列”,求
的“等比伴随数列”,求 的最大值.
的最大值.
排球队的6名队员进行传球训练,每位队员把球传给其他5人的概率相等,由甲开始传球
-
(1) 求前3次传球中,乙恰有1次接到球的概率;
-
(2) 设第
 次传球后球在乙手中的概率为
次传球后球在乙手中的概率为  ,求
,求  .
.
如图的曲线就像横放的葫芦的轴截面的边缘线,我们叫葫芦曲线(也像湖面上高低起伏的小岛在水中的倒影与自身形成的图形,也可以形象地称它为倒影曲线),它对应的方程为  其中记
其中记  为不超过
为不超过  的最大整数),且过点
的最大整数),且过点  ,若葫芦曲线上一点
,若葫芦曲线上一点  到
到  轴的距离为
轴的距离为  ,则点
,则点  到
到  轴的距离为( )
轴的距离为( )
 其中记
其中记  为不超过
为不超过  的最大整数),且过点
的最大整数),且过点  ,若葫芦曲线上一点
,若葫芦曲线上一点  到
到  轴的距离为
轴的距离为  ,则点
,则点  到
到  轴的距离为( )
轴的距离为( ) 
A .  B .
B . 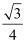 C .
C .  D .
D . 
 B .
B . 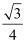 C .
C .  D .
D . 
已知函数 , 下列结论正确的是( )
, 下列结论正确的是( )
 , 下列结论正确的是( )
, 下列结论正确的是( )
A . 当 时,
时, 的图像关于y轴对称
B . 当
的图像关于y轴对称
B . 当 时,
时, 的图像关于点
的图像关于点 中心对称
C .
中心对称
C .  , 使得
, 使得 为
为 上的增函数
D . 当
上的增函数
D . 当 时,若
时,若 在
在 上单调递增,则
上单调递增,则 的最小值为
的最小值为
 时,
时, 的图像关于y轴对称
B . 当
的图像关于y轴对称
B . 当 时,
时, 的图像关于点
的图像关于点 中心对称
C .
中心对称
C .  , 使得
, 使得 为
为 上的增函数
D . 当
上的增函数
D . 当 时,若
时,若 在
在 上单调递增,则
上单调递增,则 的最小值为
的最小值为
已知向量  ,若向量
,若向量  与向量
与向量  共线,则m的值为( )
共线,则m的值为( )
 ,若向量
,若向量  与向量
与向量  共线,则m的值为( )
共线,则m的值为( )
A . -3
B . 3
C .  D .
D . 
 D .
D . 
设函数  ,则
,则  的值为.
的值为.
 ,则
,则  的值为.
的值为.
给定函数![]()
(1)试求函数![]() 的单调减区间;
的单调减区间;
(2)已知各项均为负的数列![]() 满足,
满足,![]() 求证:
求证:![]() ;
;
(3)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() 。
。
如图,菱形![]() 的边长为
的边长为![]() ,
,![]() ,
,![]() ,将菱形
,将菱形![]() 沿对角线
沿对角线![]() 折起,得到三棱锥
折起,得到三棱锥![]() ,点
,点![]() 是棱
是棱![]() 的中点,
的中点,![]() .
.
(1)求证:![]() 平面
平面![]() ;
;
(2)求证:平面![]() 平面
平面![]() ;
;
(3)求三棱锥![]() 的体积.
的体积.

已知等比数列的前n项和为Sn,且a1+a3=![]()
![]() ,则
,则![]()
![]() =
=
为了得到函数![]() 的图像,只需将函数
的图像,只需将函数![]() 的图像( )
的图像( )
A.向右平移![]() 个单位 B.向左平移
个单位 B.向左平移![]() 个单位
个单位
C.向左平移![]() 个单位 D.向右平移
个单位 D.向右平移![]() 个单位
个单位
设数列![]() 的前n 项和为
的前n 项和为![]() ,对任意
,对任意![]() 满足
满足![]() ,且
,且![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设 ,求数列
,求数列![]() 的前2n项和
的前2n项和![]() .
.
最近更新
- 如图,是平面的斜线段,为斜足。若点在平面内运动,使得的面积为定值,则动点的轨迹是( ) A、圆
- Boredwith life in the city, he moved to a remote village ___
- 染色体片段缺失是常见的染色体结构变异,缺失染色体与其正常染色体配对如下图。用显微镜检查这种改变需使用下列哪种试剂() A
- 古代诗歌阅读。(共11分) 阅读下面这首宋词,完成8~9题。 绮 怀 清·黄景仁① 几回花下坐吹箫,银汉红墙②入望遥
- (08年银川一中一模) 设=(1,-2),=(a,-1),=(-b,0),a>0,b>0,O为坐标原点,若
- 下面有关“核外电子的运动状态”的说法,错误的是()。 A.各原子轨道的伸展方向种数按p、d、f的顺序分别为3、5、7 B
- 下列有关物质分类的说法,不正确的是( )A.Na2CO3是钠盐、碳酸盐,也是正盐 B.H2SO4是含氧酸、二元酸,
- The team ________ having a meeting . A. is B. are
- 如图4-4-5所示,匀速转动的水平圆盘上,沿半径方向放着用细线连着的质量相等的物体A和B,它们与盘间的动摩擦因数相等.当
- 以下对三民主义的评述,正确的是( ) ①民族主义反映了中国人民实现民族独立的愿望;②民权主义是要建立资产阶级共和国
- 阅读下面的材料,根据要求作文。 人类已迈入21世纪。科技的高度发展,为人类提供了丰富的物质财富。但作为有血有肉有感情的人
- 在恒容密闭容器中存在下列平衡: 。 的平衡物质的量浓度与温度T的关系如右图所示。下列说法错误的是
- 下列与蛋白质、核酸相关的叙述,错误的是( ) A.一个核糖体上可以同时合成多条多肽链 B.一个蛋白质分子可以含有多
- “民主、法制、自由、人权、平等、博爱等等,这不是资本主义所特有的,这是全世界在漫长的历史过程中共同形成的文明成果,也是人
- 如图所示,两根完全相同的弹簧下挂一质量为m的小球,小球与地面间有细线相连,处于静止状态,细线竖直向下的拉力大小为2mg。
- 下列有关环境问题的说法正确的是() A.农药本身有毒,应禁止施用农药 B.推广使用脱硫煤,可以减少雾霾天气 C.用活性炭
- 该法在起草、初审、修改、再审等一系列筹备过程中,始终坚持信息公开和公众参与,整个过程完全开放,听取公众意见贯穿始终。这一
- 下图所示的实验过程中产生的现象与对应的图形不相符合的是A.向AlCl3溶液中滴加氨水至过量B.向NaOH溶液中滴入AlC
- 有机物分子中原子间(或原子与原子团间)的相互影响会导致物质化学性质的不同。下列事实不能说明上述观点的是 A.苯酚能跟Na
- 记承天寺夜游 元丰六年十月十二日夜,解衣欲睡,月色入户,欣然起行。念无与为乐者,遂至承天寺寻张怀民。怀民亦未寝,



