高中 数学
 ,
,  满足约束条件
满足约束条件 , 则
, 则 的最小值为.
的最小值为.
 在点
在点  处切线的斜率为8,则
处切线的斜率为8,则  ( )
( )
 ,
,  ,则
,则  的最小值是( )
的最小值是( )
 ,则
,则  .
.
 对应的点为
对应的点为  ,将向量
,将向量  绕原点
绕原点  按逆时针方向旋转
按逆时针方向旋转  ,所得向量对应的复数是.
,所得向量对应的复数是.
 ,
,  ;则角
;则角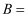 ,a的取值范围为.
,a的取值范围为.
 中的三个元素可构成某个三角形的三条边长,则此三角形一定不是( )
中的三个元素可构成某个三角形的三条边长,则此三角形一定不是( )
 的图象大致是
的图象大致是 

 B .
B .  C .
C .  D .
D . 
 、
、  、
、  为△
为△  的三内角,且角
的三内角,且角  为锐角,若
为锐角,若  ,则
,则  的最小值为.
的最小值为.
 的定义域和值域相同的是( )
的定义域和值域相同的是( )
 D . y=
D . y= 
 的值域为( )
的值域为( )
 B .
B .  C .
C .  D .
D . 
已知数列![]() 各项均为正数,且
各项均为正数,且![]() ,
,![]() .
.
(1)求数列![]() 的通项公式;
的通项公式;
(2)设![]() ,数列
,数列![]() 的前
的前![]() 项和为
项和为![]() ,求证:
,求证:![]() .
.
(2012年高考(山东理))在等差数列![]() 中,
中,![]() .
.
(Ⅰ)求数列![]() 的通项公式;
的通项公式;
(Ⅱ)对任意![]() ,将数列
,将数列![]() 中落入区间
中落入区间![]() 内的项的个数记为
内的项的个数记为![]() ,求数列
,求数列![]() 的前
的前![]() 项和
项和![]() .
.
已知函数 




① 当 

② 当 


③ 当 

④ 当 



为了调查某野生动物保护区内某种野生动物的数量,调查人员逮到这种动物1 200只作过标记后放回,一星期后,调查人员再次逮到该种动物1 000只,其中作过标记的有100只,估算保护区有这种动物________只.
已知![]() 是虚数单位,若
是虚数单位,若![]() (
(![]() ,
, ![]() ),则
),则![]() =( )
=( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
(1)求椭圆
(2)直线
- 下列有关物质的分类中正确的是选项 A B C D 名称 分类 高分子化合物 弱电解质 纯净物 混合物
- (1)图甲是某人的眼球成像示意图.请在眼球前的方框内画上合适的透镜,来矫正他的视力. (2)在图乙中画出沿斜面向
- 一列水波穿过小孔发生了衍射现象,衍射的水波与原来的水波相比( ) A.波长变短了
- 有X、Y、Z三种金属,把三种金属分别放入稀盐酸中,Y减少并放出气体,X、Z无变化;把X、Z分别放入硝酸银溶液中,X表面有
- ______ their house in London, they also have a villa in Spai
- 下面是三种组成蛋白质的氨基酸的结构式,据图分析下列叙述不正确的是()A.以上这三种氨基酸的R基依次是—H、—CH3、—C
- 我国是一个多民族的国家,下列四幅图片中,反映朝鲜族民族服饰的是哪一幅?()
- One of my students asked an amazing question, andI loved
- 细胞有丝分裂后期,由于着丝点一分为二,染色体数目暂时加倍。着丝点一分为二的原因是纺锤丝牵引的结果还是受基因控制的生理活动
- 下列最可能用于描述同一生物的一组名词是( ) A.初级消费者,第一营养级 B.次级消费者,自养型生物
- 某研究性学习小组做“水的体积随温度变化”的研究,得到如图所示的图像.从图中可知,水温度从8℃降到2℃的过程中,其密度A.
- 根据句意及首字母或汉语提示完成单词 1. Daniel is clever, but he never shows of
- 下列关于万有引力定律的说法中,不正确的是A.万有引力定律是牛顿发现的B.F=G 中的G是一个比例常数,是没有单位的C.
- 为了节省能量,某商场安装了智能化的电动扶梯。无人乘行时,扶梯运转得很慢;有人站上扶梯时,它会先慢慢加速,再匀速运转。一顾
- 进入高原地区,人们一般会产生高原反应,出现缺氧的现象,这里的“缺氧”是指缺少 A. 氧分子 B. 氧原子
- 下面是四个化学反应,你认为理论上不可用于设计原电池的化学反应是 A.Zn+Ag2O+H2O==Zn(OH)2+2Ag
- 下图为某兴趣小组制作的番茄电池,下列说法正确的是 A.电子由锌通过导线流向铜 B.该装置将电能转化为化学能
- (山东省潍坊市2015年中考地理试题)埃及是世界古代文明的发祥地之一,战略地位十分重要。读埃及图,回答下列各题。11、图
- His job is to sell the ____ carvings in the ____ department
- 化简(k∈Z).



