高中 数学
若函数  不存在极值点,则
不存在极值点,则  的取值范围是.
的取值范围是.
 不存在极值点,则
不存在极值点,则  的取值范围是.
的取值范围是.
若平面向量  满足
满足  ,且
,且  ,则
,则  可能的值有个.
可能的值有个.
 满足
满足  ,且
,且  ,则
,则  可能的值有个.
可能的值有个.
如图,⊙O是等腰三角形ABC的外接圆,AB=AC,延长BC到点D,使CD=AC,连接AD交⊙O于点E,连接BE与AC交于点F.

-
(1) 判断BE是否平分∠ABC,并说明理由;
-
(2) 若AE=6,BE=8,求EF的长.
sin810°+cos(﹣60°)=( )
A .  B . ﹣
B . ﹣  C .
C .  D .
D . 
 B . ﹣
B . ﹣  C .
C .  D .
D . 
已知  ,若存在
,若存在  ,使不等式
,使不等式  成立,则
成立,则  的取值范围是( )
的取值范围是( )
 ,若存在
,若存在  ,使不等式
,使不等式  成立,则
成立,则  的取值范围是( )
的取值范围是( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
数列  是等差数列,
是等差数列,  为其前n项和,且
为其前n项和,且 
 是等差数列,
是等差数列,  为其前n项和,且
为其前n项和,且 
(Ⅰ)求数列  的通项公式;
的通项公式;
(Ⅱ)设数列  是首项为1,公比为2的等比数列,求数列
是首项为1,公比为2的等比数列,求数列  的前n项和
的前n项和 
设 的内角A、B、C的对边分别是a、b、c,若
的内角A、B、C的对边分别是a、b、c,若 , 则
, 则 的形状是( )
的形状是( )
 的内角A、B、C的对边分别是a、b、c,若
的内角A、B、C的对边分别是a、b、c,若 , 则
, 则 的形状是( )
的形状是( )
A . 等边三角形
B . C为直角的直角三角形
C . C为顶角的等腰三角形
D . A为顶角的等腰三角形或B为顶角的等腰三角形
(理科)某工厂在试验阶段生产出了一种零件,该零件有A、B两项技术指标需要检测,设各项技术指标达标与否互不影响.若有且仅有一项技术指标达标的概率为 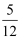 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为  .按质量检验规定:两项技术指标都达标的零件为合格品.则一个零件经过检测,为合格品的概率是.
.按质量检验规定:两项技术指标都达标的零件为合格品.则一个零件经过检测,为合格品的概率是.
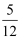 ,至少一项技术指标达标的概率为
,至少一项技术指标达标的概率为  .按质量检验规定:两项技术指标都达标的零件为合格品.则一个零件经过检测,为合格品的概率是.
.按质量检验规定:两项技术指标都达标的零件为合格品.则一个零件经过检测,为合格品的概率是.
设△ABC的内角A,B,C的所对边分别为a,b,c,已知sin2(B+C)=sin2B﹣sinBsinC+sin2C.
-
(1) 求cosA;
-
(2) 若c=
 ,求sinC.
,求sinC.
过点  ,且在
,且在  轴上的截距是在
轴上的截距是在  轴上截距的2倍的直线方程是( )
轴上截距的2倍的直线方程是( )
 ,且在
,且在  轴上的截距是在
轴上的截距是在  轴上截距的2倍的直线方程是( )
轴上截距的2倍的直线方程是( )
A .  B .
B .  或
或  C .
C .  D .
D .  或
或 
 B .
B .  或
或  C .
C .  D .
D .  或
或 
已知函数  ,
,  .
.
 ,
,  .
.
-
(1) 若
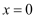 恰为
恰为  的极小值点.
的极小值点. ①证明:
 ;
;②求
 在区间
在区间  上的零点个数;
上的零点个数; -
(2) 若
 ,
,  ,又由泰勒级数知:
,又由泰勒级数知:  ,证明:
,证明: 
已知函数  是定义在
是定义在  上的偶函数,且当
上的偶函数,且当  时,
时,  的图象如图所示,则
的图象如图所示,则  的值域是( )
的值域是( )
 是定义在
是定义在  上的偶函数,且当
上的偶函数,且当  时,
时,  的图象如图所示,则
的图象如图所示,则  的值域是( )
的值域是( ) 
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知函数f(x)=ex﹣1+ax,a∈R.
-
(1) 讨论函数f(x)的单调区间;
-
(2) 若∀x∈[1,+∞),f(x)+lnx≥a+1恒成立,求a的取值范围.
在三棱柱ABC﹣A1B1C1中,D是CC1的中点,F是A1B的中点,且  ,则( )
,则( )
 ,则( )
,则( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
已知直线  平面
平面  ,直线
,直线  平面
平面  ,则下列四个命题正确的是( )
,则下列四个命题正确的是( )
 平面
平面  ,直线
,直线  平面
平面  ,则下列四个命题正确的是( )
,则下列四个命题正确的是( )  ;
;  ;
;  ;
;  .
.
A .  B .
B .  C .
C .  D .
D . 
已知双曲线![]() 的离心率为3,焦点到渐近线的距离为
的离心率为3,焦点到渐近线的距离为![]() ,则此双曲线的焦距等于 ( )
,则此双曲线的焦距等于 ( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
.已知向量![]() =(2,4,x),
=(2,4,x),![]() =(2,y,2),若
=(2,y,2),若![]() ,则x+y的值是( )
,则x+y的值是( )
A.﹣3或1 B.3或1 C.﹣3 D.1
设集合![]() ,
,![]() ,则
,则![]() ( )
( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
已知椭圆 的离心率为
的离心率为 ,以原点为圆心,椭圆的短半轴为长为半径的圆与直线
,以原点为圆心,椭圆的短半轴为长为半径的圆与直线 相切,过点
相切,过点 的直线
的直线 与椭圆
与椭圆 相交于
相交于 两点.
两点.
(1)求椭圆 的方程;
的方程;
(2)若原点 在以线段
在以线段 为直径的圆内,求直线
为直径的圆内,求直线 的斜率
的斜率 的取值范围.
的取值范围.
(1)求椭圆
(2)若原点
最近更新
- 要得到番茄的无籽果实,需将一定浓度的生长素类似物溶液滴在雌蕊的柱头上。处理的时间和条件是 A.花蕾期,不去雄蕊
- 下列有关生态系统稳定性的叙述,不正确的是( ) A.生态系统具有自我调节能力,这是生态系统稳定性的基础 B.生态系
- 下列命题中,不能体现辨证法思想的有 A.“穷则变,变则通,通则久”B.“祸兮福之所倚,福兮祸之所伏”C.“道之大原出于天
- 某同学帮助校园绿化工人做花圃土壤分析,结果发出其pH小于7,为改食土壤应摆选择的物质是
- is Mr. Green’s bus? It’s No.20. A.What’s number
- 一质点沿直线运动,第1 s内通过1 m,第2 s内通过2 m,第3 s内通过3 m,第4 s内通过4 m.该质点的运动可
- 某自来水厂用源水处理成自来水的流程如下:(1)加入活性炭的作用是 ;在乡村没有活性炭,常加入
- 某元素位于周期表中的ⅣA族,它是良好的半导体材料,其金属性比非金属性强,所以通常认为它是金属元素。此元素可能是(
- 将含有草履虫的池塘水置于烧杯中,不久就会发现草履虫都集中在水的表层,原因是草履虫需要( ) A.阳光
- 如图,画出两条入射光线对应的折射光线。(保留必要的作图痕迹)。
- 下面两幅图片反映的两种政治制度最主要的区别是 ()宁夏回族自治区成立50周年纪念币 港特别行政区区徽 A.社
- 阅读下文,完成下面题目。(12分)普少习吏事,寡学术,及为相,太祖常劝以读书。晚年手不释卷,每归私第,阖户启箧取书,读之
- 名句默写 1、 ,悠悠我心。 2、 ,
- 名著阅读。 桑桑(《草房子》) 冯歪嘴子(《呼兰河传》) 圣地亚哥(《老人与海》) 请从上面三个人物形象中任选一个,结合
- 下列叙述符合由赤道向两极的地域分异规律的是( ) A. 自然带随纬度变化方向更替 B.
- 2009年是我国改革开放31周年。31年前,党的十一届三中全会提出以经济建设为中心,大力发展生产力。为了发展生产力,必须
- 函数f(x)=ax (a>0, a≠1)在[1, 2]中的最大值比最小值大, 则a的值为 .
- 根从土壤中吸水,土壤里的水分通过根向上输送到茎的途径是( ) A.土壤水分→导管→根毛→根毛区表皮细胞以内的各层
- 已知A、B两点在数轴上表示的数为a和b,M、N均为数轴上的点,且OA<OB.(1)若A、B的位置如图l所示,试化简
- 小明观察了市场上的测重仪后,设计了如图5四个电路(R是定值电阻,R1是滑动变阻器).可以测量人体重的电路是(



