高中 数学
某校从参加高一年级期中考试的学生中抽出60名学生,将其数学成绩(均为整数)分成六段[40,50),[50,60)…,[80,90),[90,100],然后画出如图所示部分频率分布直方图.观察图形的信息,回答下列问题:

-
(1) 求第四小组的频率,并补全这个频率分布直方图;
-
(2) 估计这次考试的及格率(60分及60分以上为及格)和平均分;
-
(3) 把从[80,90)分数段选取的最高分的两人组成B组,[90,100]分数段的学生组成C组,现从B,C两组中选两人参加科普知识竞赛,求这两个学生都来自C组的概率.
三棱柱ABC﹣A1B1C1中,CC1⊥平面ABC,△ABC是边长为4的等边三角形,D为AB边中点,且CC1=2AB.

-
(1) 求证:平面C1CD⊥平面ABC;
-
(2) 求证:AC1∥平面CDB1;
-
(3) 求三棱锥D﹣CAB1的体积.
已知双曲线  的左右焦点为
的左右焦点为  ,过左焦点
,过左焦点  作垂直于
作垂直于  轴的直线交 双曲线的两条渐近线于
轴的直线交 双曲线的两条渐近线于 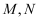 两点,若
两点,若  是直角,则双曲线的离心率是( ).
是直角,则双曲线的离心率是( ).
 的左右焦点为
的左右焦点为  ,过左焦点
,过左焦点  作垂直于
作垂直于  轴的直线交 双曲线的两条渐近线于
轴的直线交 双曲线的两条渐近线于 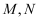 两点,若
两点,若  是直角,则双曲线的离心率是( ).
是直角,则双曲线的离心率是( ).
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
化简sin600°的值是( )
A . 0.5
B . -0.5
C .  D .
D . 
 D .
D . 
如图所示,给出4个幂函数的图象,则图象与函数的大致对应是( )




A . ①  ,②
,② 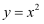 ,③
,③  ,④
,④  B . ①
B . ①  ,②
,② 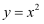 ,③
,③  ,④
,④  C . ①
C . ① 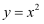 ,②
,②  ,③
,③  ,④
,④  D . ①
D . ①  ,②
,②  ,③
,③ 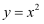 ,④
,④ 
 ,②
,② 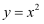 ,③
,③  ,④
,④  B . ①
B . ①  ,②
,② 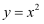 ,③
,③  ,④
,④  C . ①
C . ① 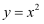 ,②
,②  ,③
,③  ,④
,④  D . ①
D . ①  ,②
,②  ,③
,③ 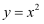 ,④
,④ 
如图是为求S=1+  +
+  +…
+… 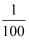 的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.
的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.
 +
+  +…
+… 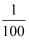 的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.
的和而设计的程序框图,将空白处补上,指明它是循环结构中的哪一种类型,并画出它的另一种循环结构框图.如图是当型循环结构.
已知函数f(x)为奇函数,且当x>0时,  ,则f(-4)=.
,则f(-4)=.
 ,则f(-4)=.
,则f(-4)=.
定义在R上的偶函数f(x)满足:对任意的x1 , x2∈[0,+∞)(x1≠x2),有 , 则( )
, 则( )
 , 则( )
, 则( )
A . f(3)<f(-2)<f(1)
B . f(1)<f(-2)<f(3)
C . f(-2)<f(1)<f(3)
D . f(3)<f(1)<f(-2)
已知复数  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A . -3
B . -1
C . 1
D . 3
已知等差数列  的首项为1,且
的首项为1,且  ,则
,则  ( )
( )
 的首项为1,且
的首项为1,且  ,则
,则  ( )
( )
A . 2
B . 3
C . 4
D . 0
双曲线x2﹣  =1位于第一象限内的点P到该双曲线的右焦点的距离为2,则由双曲线的两焦点及点P构成的三角形面积S=( )
=1位于第一象限内的点P到该双曲线的右焦点的距离为2,则由双曲线的两焦点及点P构成的三角形面积S=( )
 =1位于第一象限内的点P到该双曲线的右焦点的距离为2,则由双曲线的两焦点及点P构成的三角形面积S=( )
=1位于第一象限内的点P到该双曲线的右焦点的距离为2,则由双曲线的两焦点及点P构成的三角形面积S=( )
A .  B . 4
C . 2
B . 4
C . 2  D . 5
D . 5
 B . 4
C . 2
B . 4
C . 2  D . 5
D . 5
已知函数f(x)=|x﹣1|+|x﹣a|
-
(1) 若函数f(x)的值域为[2,+∞),求实数a的值
-
(2) 若f(2﹣a)≥f(2),求实数a的取值范围.
已知函数  ,
,  .
.
 ,
,  .
.
-
(1) 求函数
 的图象与直线
的图象与直线  围成区域的面积;
围成区域的面积;
-
(2) 若对于
 ,
,  ,且
,且  时,不等式
时,不等式  恒成立,求实数
恒成立,求实数  的取值范围.
的取值范围.
如图,四棱柱  的底面ABCD为矩形,
的底面ABCD为矩形,  ,M为BC中点,平面
,M为BC中点,平面  ,
,  且
且  .
.
 的底面ABCD为矩形,
的底面ABCD为矩形,  ,M为BC中点,平面
,M为BC中点,平面  ,
,  且
且  .
. 
-
(1) 证明:
 .
.
-
(2) 若此四棱柱的体积为2求二面角
 的正弦值.
的正弦值.
若不等式  的解集是区间
的解集是区间  的子集,则实数
的子集,则实数  的取值范围为.
的取值范围为.
 的解集是区间
的解集是区间  的子集,则实数
的子集,则实数  的取值范围为.
的取值范围为.
设集合A={x|0<x﹣m<2},B={x|﹣x2+3x≤0},分别求满足下列条件的实数m的取值范围:
(1)A∩B=∅;
(2)A∪B=B.
已知  ,则
,则  的大小关系为( )
的大小关系为( )
 ,则
,则  的大小关系为( )
的大小关系为( )
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
某品牌手机厂商推出新款的旗舰机型,并在某地区跟踪调查得到这款手机上市时间(![]() 个月)和市场占有率(
个月)和市场占有率(![]() )的几组相关对应数据;
)的几组相关对应数据;
|
| 1 | 2 | 3 | 4 | 5 |
|
| 0.02 | 0.05 | 0.1 | 0.15 | 0.18 |
(1)根据上表中的数据,用最小二乘法求出![]() 关于
关于![]() 的线性回归方程;
的线性回归方程;
(2)根据上述回归方程,分析该款旗舰机型市场占有率的变化趋势,并预测自上市起经过多少个月,该款旗舰机型市场占有率能超过![]() (精确到月)
(精确到月)
附: .
.
 如图,正方形
如图,正方形![]() 中,
中,![]() 、
、![]() 分别是
分别是![]() 、
、![]() 的中点,若
的中点,若![]() ,则
,则![]() ( )
( )
A.2 B.![]()
C.![]() D.
D.![]()
已知函数 ,则( )
,则( )
A. 是奇函数,且在
是奇函数,且在 上单调递增
上单调递增
B. 是奇函数,且在
是奇函数,且在 上单调递减
上单调递减
C. 是偶函数,且在
是偶函数,且在 上单调递增
上单调递增
D. 是偶函数,且在
是偶函数,且在 上单调递减
上单调递减
A.
B.
C.
D.
最近更新
- (12分)在HF、H2S、PCl3、CS2、CF4、N2分子中:(1)以非极性键结合的非极性分子是________。(2
- 根据句意及首字母提示,填写单词。 1. I’d like to have two applep________. 2.
- 一个工厂生产一种产品,现在的成本是37.4元,比原来的成本降低了15%,原来的成本是多少?
- 水稻是我国南方地区的主要粮食作物之一。下列最早大量种植这种作物的原始农耕居民是( ) A.元谋人 B
- The heavy rain stopped thechildren ______ to the park. A. t
- 科学家最近制得了一种新型的氧分子O4,以下叙述正确的是A. O2、O3和O4都是单质 B. O4是由O2组成的混合物 C
- 有下列8种物质: A.干冰 B.氧化镁 C.氯化铵
- 下列关于苯的叙述正确的是A. 反应①为取代反应,有机产物与水混合浮在上层 B. 反应②为氧化反应,反应现象是火焰明亮并
- 语言知识及运用;从各题所给的A、B、C和D项中,选出可以填入空白处的最佳选项。Hurryup, kids! The sc
- 若函数y=kx+b的图象平行于直线y=-2x+1且与y轴的交点坐标为(0,—5),则函数的表达式是
- 在敲响大古钟时发现,停止了对大钟的撞击后,大钟“余音不止”,原因是( )A.人的听觉暂留 B.是大钟
- Men Xue and Yang Yue are good friends.They are in the same s
- (08年西南师大附中期末)(6分) 如图所示为“研究电磁感应现象”的实验装置:B为直径较大的螺线管、A为直径较小的螺线管
- “重男轻女”本来是中国封建社会的思想意识,是生产资料私有制财产继承关系的反映,但时至今日,这种思想依然残留在一些人的头脑
- 如图所示.三棱柱A。B。C1―ABC的侧面BCC1B1是菱形,∠CBB1=60°,AB⊥面BCClB1,AB=3,BB1
- 若,则=________.
- 科学家通过对前列腺癌细胞的研究发现,绿茶具有抗癌作用。绿茶中的多酚可以减少人体的BCL-XL蛋白,而这种蛋白质有抑制癌细
- 已知|a|<1,|b|<1,求证:<1.
- 生活经验和学习对动物的后天性行为的形成起着决定性作用。动物建立后天性行为的主要方式是( ) A.非条件反射 B
- 下表列出几种金属的资料,利用这些资料回答以下问题。金属导电性导热性成本($/kg)抗腐蚀性密度/g·cm-3强度钠很好好



