高中 数学
数列  的前49项和为
的前49项和为
 的前49项和为
的前49项和为
设抛物线  的焦点为
的焦点为  ,
,  、
、  两点在抛物线上,且
两点在抛物线上,且  、
、  、
、  三点共线,过
三点共线,过  的中点
的中点  作
作  轴的垂线与抛物线在第一象限内交于点
轴的垂线与抛物线在第一象限内交于点  ,若
,若  ,则
,则  ( )
( )
 的焦点为
的焦点为  ,
,  、
、  两点在抛物线上,且
两点在抛物线上,且  、
、  、
、  三点共线,过
三点共线,过  的中点
的中点  作
作  轴的垂线与抛物线在第一象限内交于点
轴的垂线与抛物线在第一象限内交于点  ,若
,若  ,则
,则  ( )
( )
A . 4
B . 6
C . 8
D . 10
已知函数  ,则
,则  ( )
( )
 ,则
,则  ( )
( )
A . 是奇函数,且在  上单调递增
B . 是奇函数,且在
上单调递增
B . 是奇函数,且在  上单调递减
C . 是偶函数,且在
上单调递减
C . 是偶函数,且在  上单调递增
D . 是偶函数,且在
上单调递增
D . 是偶函数,且在  上单调递减
上单调递减
 上单调递增
B . 是奇函数,且在
上单调递增
B . 是奇函数,且在  上单调递减
C . 是偶函数,且在
上单调递减
C . 是偶函数,且在  上单调递增
D . 是偶函数,且在
上单调递增
D . 是偶函数,且在  上单调递减
上单调递减
若  ,则
,则  的值为( )
的值为( )
 ,则
,则  的值为( )
的值为( )
A . 4
B . 5
C . 6
D . 7
2021年某省新高考将实行“  ”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件
”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件  :“他选择政治和地理”,事件
:“他选择政治和地理”,事件  :“他选择化学和地理”,则事件
:“他选择化学和地理”,则事件  与事件
与事件  ( )
( )
 ”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件
”模式,即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,共有12种选课模式.某同学已选了物理,记事件  :“他选择政治和地理”,事件
:“他选择政治和地理”,事件  :“他选择化学和地理”,则事件
:“他选择化学和地理”,则事件  与事件
与事件  ( )
( )
A . 是互斥事件,不是对立事件
B . 是对立事件,不是互斥事件
C . 既是互斥事件,也是对立事件
D . 既不是互斥事件也不是对立事件
如甲图所示,在矩形ABCD中,AB=4,AD=2,E是CD的中点,将△ADE沿AE折起到△D1AE位置,使平面D1AE⊥平面ABCE,得到乙图所示的四棱锥D1﹣ABCE.
(Ⅰ)求证:BE⊥平面D1AE;
(Ⅱ)求二面角A﹣D1E﹣C的余弦值.

某学校为了对教师教学水平和教师管理水平进行评价,从该校学生中选出100人进行统计,其中对教师教学水平满意的学生人数为总数的60%,对教师管理水平满意的学生人数为总数的75%,对教师教学水平和教师管理水平都满意的有40人.
参考公式: , 其中
, 其中 .
.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
k | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
-
(1) 完成对教师教学水平和教师管理水平评价的2×2列联表,并判断是否有97.5%的把握认为对教师教学水平满意与教师管理水平满意有关;
对教师管理水平满意
对教师管理水平不满意
合计
对教师教学水平满意
对教师教学水平不满意
合计
-
(2) 若将频率视为概率,随机从学校中抽取3人参与此次评价,设对教师教学水平和教师管理水平都满意的人数为随机变量X;求X的分布列和数学期望.
曲线  在点
在点  处的切线的斜率为
处的切线的斜率为 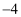 ,则
,则  ( )
( )
 在点
在点  处的切线的斜率为
处的切线的斜率为 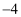 ,则
,则  ( )
( )
A . 2
B . -3
C . -7
D . -10
如图,点M,N分别在对角线  上,且
上,且  .求证:向量
.求证:向量  共面.
共面.
 上,且
上,且  .求证:向量
.求证:向量  共面.
共面. 
在正四面体ABCD中,M,N分别是BC和DA的中点,则异面直线MN和CD所成角为.
抛掷两枚质地均匀的硬币,下列事件与事件“至少一枚硬币正面朝上”互为对立的是( )
A . 至多一枚硬币正面朝上
B . 只有一枚硬币正面朝上
C . 两枚硬币反面朝上
D . 两枚硬币正面朝上
如图,三棱锥  中,
中,  的边长为2的正三角形,
的边长为2的正三角形,  是以
是以  为直角顶点的等腰直角三角形.补充条件:①
为直角顶点的等腰直角三角形.补充条件:①  ;② 点
;② 点  在平面
在平面  内的射影是
内的射影是  的外心.
的外心.
 中,
中,  的边长为2的正三角形,
的边长为2的正三角形,  是以
是以  为直角顶点的等腰直角三角形.补充条件:①
为直角顶点的等腰直角三角形.补充条件:①  ;② 点
;② 点  在平面
在平面  内的射影是
内的射影是  的外心.
的外心. 
-
(1) 从补充条件①,②任选一个(只能选一个)结合已知条件, 证明:平面
 ⊥平面
⊥平面  ;
;
-
(2) 在(1)成立的情况下,过
 的平面交
的平面交  于点
于点  ,若平面
,若平面  把三棱锥
把三棱锥  分成体积相等的两部分,求锐二面角
分成体积相等的两部分,求锐二面角  的余弦值.
的余弦值.
如图,平面 平面CEFG,四边形CEFG中,
平面CEFG,四边形CEFG中, ,
,  , 点E在正方形ACDE的外部,且
, 点E在正方形ACDE的外部,且 ,
,  ,
,  ,
,  .
.
 平面CEFG,四边形CEFG中,
平面CEFG,四边形CEFG中, ,
,  , 点E在正方形ACDE的外部,且
, 点E在正方形ACDE的外部,且 ,
,  ,
,  ,
,  .
. 
-
(1) 证明:
 ;
;
-
(2) 求二面角
 的余弦值.
的余弦值.
设变量x,y满足  .若z=a2x+y(a>0)的最大值为 4.则 a=.
.若z=a2x+y(a>0)的最大值为 4.则 a=.
 .若z=a2x+y(a>0)的最大值为 4.则 a=.
.若z=a2x+y(a>0)的最大值为 4.则 a=.
给定两个命题:  :对任意实数
:对任意实数  都有
都有  恒成立;
恒成立;  :关于
:关于  的方程
的方程  有实数根;若
有实数根;若  为真命题,
为真命题,  为假命题,求实数
为假命题,求实数  的取值范围.
的取值范围.
 :对任意实数
:对任意实数  都有
都有  恒成立;
恒成立;  :关于
:关于  的方程
的方程  有实数根;若
有实数根;若  为真命题,
为真命题,  为假命题,求实数
为假命题,求实数  的取值范围.
的取值范围.
如图,在菱形 中,
中, ,
,  ,
,  是
是 的中点,将
的中点,将 沿直线
沿直线 翻折至
翻折至 的位置,使得面
的位置,使得面  面
面 , 则点
, 则点 到直线
到直线 的距离为
的距离为
 中,
中, ,
,  ,
,  是
是 的中点,将
的中点,将 沿直线
沿直线 翻折至
翻折至 的位置,使得面
的位置,使得面  面
面 , 则点
, 则点 到直线
到直线 的距离为
的距离为
A .  B .
B .  C .
C .  D .
D . 
 B .
B .  C .
C .  D .
D . 
用反证法证明“如果整系数一元二次方程ax2+bx+c=0(a≠0)有有理数根,那么a,b,c中至少有一个偶数”时,下列假设正确的是( )
A. 假设a,b,c都是偶数 B. 假设a,b,c都不是偶数
C.假设a,b,c至多有一个偶数 D. 假设a,b,c至多有两个偶数
已知向量a![]() ,b
,b![]() ,且
,且![]() .
.
(1)求a·b和|a+b|;
(2)若函数![]() a·b +|a+b| 有零点,求实数
a·b +|a+b| 有零点,求实数![]() 的取值范围.
的取值范围.
发行体育彩卷,号码从000001到999999,购买后揭号对奖,若规定:从个位数起,第一、 三、五位是不同的奇数,第二、四、六位均为偶数时为中奖号码,则中奖面为
A.0.75% B.0.36% C.15.63% D.36.26%
等比数列{an}中,已知![]() a1=2,a
a1=2,a![]() 4=16.
4=16.
(1)求数列{an}的通项公式an;
(2)若a3,a5分别是等差数列{bn}的第4项和第16项,求数列{bn}的通项公式及前n项和Sn.
最近更新
- 6.对地震灾情进行监测和受灾情况的统计,主要是利用了() A.RS和GPS B.RS和GIS C.G
- (1)下列每组物质中都有一种与其它三种不同类,找出这种物质将其化学式写在后面的横线上: ①NaCl、NaI、Na2CO
- The shopkeeper did not want to sell for he thought
- 17~18世纪,出现了许多的启蒙思想家,他们的理论启迪了人们的思想,人们把他们提倡的思想称为 A.人文主义
- 通过基因工程的方法,科学家采用花粉管通道法将毒蛋白基因转入棉花植株并获得成功表达.棉铃虫吃了这种转基因棉花的植株后就会死
- 下表(一)是对上海、哈尔滨两地居民择偶标准的调查统计,对其解读不正确的是 表一:上海、哈尔滨不同年代择偶标准差异表
- 141. According to recent reports, one of the rare animals, _
- If you plan on visiting to Fiji, you are probably looking fo
- 3个不同的氨基酸可以合成三肽的种类,以及三种不同的氨基酸数量足够时能合 成的三肽的种类分别是( ) A.3、9
- 依次填入下列各句中横线处的词语,最恰当的一组是 ( ) ①在得知老区受灾的消
- 生活中难免会遇到一些突发事件,我们要善于利用学过的知识,采取科学、有效的方法保护自己。如果发生了氯气泄漏,以下自救方法得
- 阅读下面的文字,完成下列各题。陕北的山陕北真是一个神奇而美妙的地方。说它神奇而美妙,更多的是因为它的山—&m
- 设NA为阿伏加德罗常数值,下列说法正确的是( ) A.2 mL 0.5 mol/L FeCl3溶液滴入沸水中制备F
- 科学探测表明,月球上至少存在着丰富的氧、硅、铝、铁等资源,设想人类开发月球,不断把月球上的矿藏搬运到地球上.假定经过长期
- 现有下列数据,用对应的序号填空(5分) A. 45° B. 90° C. 2/3 D. 1/3 E. 1/
- 甲烷分子是以碳原子为中心的正四面体结构,而不是正方形的平面结构,理由是( )A.CH3Cl只有一种空间结构
- 2010年2月,由中国教育报和中国教育电视台联合主办的“2009年度中国教育新闻人物”评选结果揭晓,钱学森获得了“中国教
- 依次填入下列各句横线处的词语,最恰当的一组是 ()①北京市政府对城市建设布局做出了________,在2010年
- 梭伦改革中依据财产等级制度的划分,下列哪个阶层获得的利益最多 A.贵族 B.平民 C.奴隶 D.工商业
- 某种鼠中,黄鼠基因A对灰鼠基因a为显性,短尾基因B对长尾基因b显性。且基因A或b在纯合时使胚胎致死,这两对基因是独立遗传




